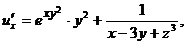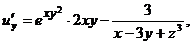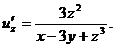Глава V. Функции нескольких переменных

Понятие n-мерного координатного пространства

Определение 5.1.

Множество всевозможных упорядоченных совокупностей (х₁, х₂, …, х_n) n вещественных чисел называется n-мерным координатным пространством и обозначается .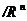

Каждая упорядоченная совокупность(х₁, х₂, …, х_n) называется точкой пространства 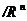и обозначается буквой М или М(х₁, х₂, …, х_n).

При этом числа х₁, х₂, …, х_n называются координатами точки М.

Замечание 5.1.

Важными частными случаями координатного пространства являются пространство 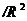упорядоченных пар вещественных чисел (х, у) и пространство 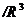упорядоченных троек вещественных чисел (х, у, z).

Определение 5.2.

Рассмотрим 2 точки М'(х₁', х₂', …, х_n') и М''(х₁'', х₂'', …, х_n'') координатного пространства .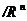

Расстоянием между точками М' и М'' называется число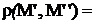

= .

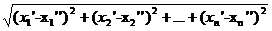Определение 5.3.

Множество точек М 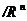, для которых выполнено условие 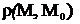< R, называется открытым n-мерным шаром радиуса R с центром в точке М₀.

Определение 5.4.

Открытый n-мерный шар радиуса δ с центром в точке М₀ называется δ-окрестностью точки М_0.

Обозначение: О_δ(М₀).

Таким образом, О_δ(М₀) = {M 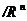: ρ(M, M₀) < δ}.

Замечание 5.2.

При n = 2 δ-окрестностью точки М₀(х₀, у₀) является открытый круг О_δ(М₀) = {(х, у) 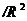: (х-х₀)² + (у-у₀)² < δ²} (рис. 5.1).

При n = 3 δ-окрестностью точки М₀(х₀, у₀, z₀) является открытый шар О_δ(М₀)= {(х, у, z) 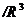: (х-х₀)² + (у-у₀)² + (z-z₀)² < δ²}.

Определение функции нескольких переменных

Определение 5.5.

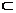
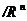Пусть каждой точке М(х₁, х₂, …, х_n) Х по некоторому правилу f сопоставлено единственное число u из числового множества U, тогда говорят, что на множестве Х задана функция n переменных.

Обозначение: f(х₁, х₂, …, х_n) или u = f(х₁, х₂, …, х_n).

(Другие обозначения: f(М) или u = f(М)).

Множество Х называется областью определения функции f(M) и обозначается D(f).

Числа х₁, х₂, …, х_n называются независимыми переменными или аргументами функции.

Замечание 5.3.

Функции двух и трех переменных в дальнейшем будем обозначать f(x, y) (z = f(x, y)) и f(x, y, z) (u = f(x, y, z)) соответственно.

Определение 5.6.

Графиком функции f(х₁, х₂, …, х_n) называется множество точек {( х₁, х₂, …, х_n, u) /Rⁿ⁺¹ : (х₁, х₂, …, х_n) X, u = f(х₁, х₂, …, х_n)}.

Обозначение: Г(f).

Определение 5.7.

Линией уровня функции f(х₁, х₂, …, х_n) называется множество точек, координаты которых удовлетворяют уравнению f(х₁, х₂, …, х_n) = с, где с – некоторое фиксированное число.

Функции двух и трех переменных можно изучать с помощью их графиков и линий уровня.

Пример 5.1.

Рассмотрим функцию f(x, y) = x² + y².

График Г(f) этой функции представляет собой поверхность в /R³, заданную уравнением z = x² + y². Эта поверхность называется параболоидом вращения (рис. 5.2).

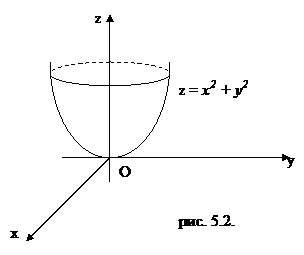
Линии уровня данной функции образуют семейство кривых на плоскости хОу, описываемое уравнением x² + y² = с.

у

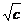Если с > 0, то уравнение описывает семейство концентрических окружностей с центром в точке О(0, 0) и радиусом (рис.5.3). При с = 0 окружность вырождается в точку О(0, 0), а при с < 0 рассматриваемое уравнение задаем пустое множество.

	рис. 5.3.

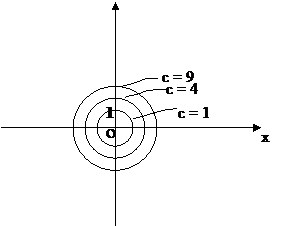Замечание 5.4.

Для функции нескольких переменных можно ввести понятия предела функции в точке, пределов по направлению (они являются обобщениями понятия односторонних пределов для функции одной переменной), непрерывности функции в точке и на замкнутом ограниченном множестве.

Более подробно с этим понятиеми можно познакомиться в [1] (глава 15, п. 15.2).

Частные производные функции

Определение 5.8.

Пусть функция u=f(x₁,x₂,…,x_n) задана в некоторой окрестности точки M₀(x₁⁰,x₂⁰,…,x_n⁰).

Частной производной функции f(x₁,x₂,…,x_n) по аргументу x_k в точке M₀ называется производная функции f(x₁⁰,x₂⁰,…,x_k,…,x_n⁰) в точке х_к⁰.

Обозначение: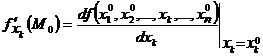

(Другие обозначения: ).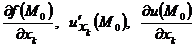

Определение 5.9.

1. Приращением аргумента x_k в точке x_k⁰ называется выражение .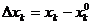

2. Частным приращением функции f(x₁,x₂,…,x_n) по аргументу x_k в точке

M₀(x₁⁰,x₂⁰,…,x_n⁰) называется выражение f(x₁⁰,x₂⁰,…,x_k⁰+ 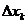,…,x_n⁰) -

- f(x₁⁰,x₂⁰,…,x_k⁰,…,x_n⁰), которое обозначается .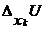

Таким образом, .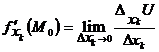

Замечание 5.5.

Если частная производная функции f(x₁,x₂,…,x_n) по аргументу x_k существует для всех точек некоторого множества Х, то сопоставив каждой точке 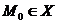значение 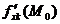, получим функцию n переменных, которая называется частной производной функции f(x₁,x₂,…,x_n) по аргументу x_k и обозначается f'_xk.

(Другие обозначения: ).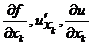

Вычисления частных производных производится по обычным правилам вычисления производных функций одной переменной.

Пример 5.2.

Вычислим частные производные функции .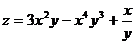

При нахождении частной производной по аргументу x исходную функцию рассматриваем как функцию одной переменной x при фиксированном значении переменной .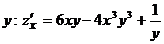

Повторим ту же процедуру, меняя роли x и .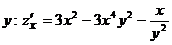

Пример 5.3.

Частные производные функции трёх переменных 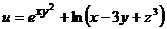выражаются следующим формулами: