Последовательность и ее предел

Определение 2.1.

Пусть любому натуральному числу n сопоставлено в соответствие вещественное число х 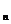, тогда говорят, что задана последовательность ,…

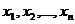Обозначение: { х }.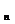

Числа 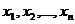,… называются членами последовательности, n-ый член х 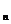называется общим членом последовательности.

Замечание 2.1.

Последовательность можно рассматривать как некоторую функцию f, область определения которой есть множество натуральных чисел /N, при этом х 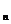= f (х 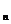) для любых n /N.

Пример 2.1.

Рассмотрим последовательность 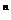{q } (q 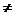0). Такая последовательность называется геометрической прогрессией.

В развернутом виде она может быть записана, например, при q= 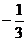в виде:

…

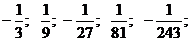Пример 2.2. (Последовательность Фибоначчи)

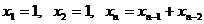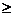(n 3).

Такая последовательность задана рекуррентной формулой, позволяющей находить члены последовательности по известным предыдущим.

Определение 2.2.

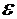Пусть а, 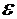- вещественные числа, причем 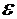>0. –окрестностью точки а называется интервал 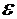(а- , а + ).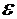

Обозначение: 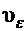(а).

Определение 2.3.

Число а называется пределом последовательности {х 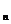}, если какую бы малую

окрестность 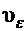(а) ни взять, все точки х 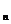с достаточно большими номерами (n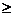 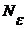) попадут в эту окрестность, причем вне этой окрестности может остаться лишь конечное число точек, изображающих члены последовательности.

Если последовательность {х 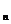} имеет конечный предел а, то говорят, что данная последовательность сходится к числу а.

Обозначение: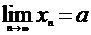

Пример 2.3.

Рассмотрим последовательность , или в развернутом виде …

.

.

.

.

.

.

.

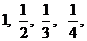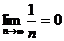Докажем, что . Пусть, например, 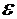= 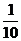. Построим окрестность 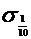(0) точки О.

Рис. 2.1

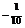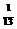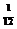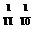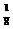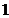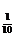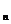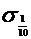Из рисунка 2.1. видно, что начиная с номера N =11 все точки х = попадают в окрестность (0).

Аналогичные рассуждения можно провести и для любых других значений 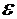. Таким образом, .

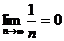Предел функции в точке. Односторонние пределы

Определение 2.4. (предела функции на языке последовательностей).

Пусть функция f(x) определена в некоторой окрестности точке x₀ за исключением возможно самой точки x₀. Число а называется пределом функции f(x) в точке x₀, если для любой последовательности {х 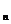}, сходящейся к x₀ (x_n 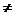x₀), соответствующая последовательность {f (х 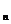)} сходится к числу а. При этом предполагается, что все x_n принадлежат рассматриваемой окрестности точки x₀.

Определение 2.5. (предела функции на формальном языке).

Пусть функция f(x) определена в некоторой окрестности точки x₀ за

исключением возможно самой точки x₀. Число а называется пределом функции f(x) в точке x₀, если для любого положительного числа 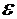существует положительное число 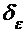такое, что 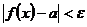, если .

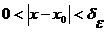Обозначение: .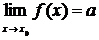

Пример 2.4.

Доказать, что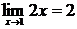

Решение

Рассмотрим положительное число 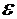. Неравенство 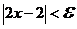равносильно неравенству 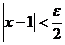. Положим 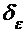= 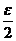, тогда если 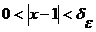, то 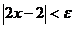, следовательно, .

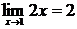Определение 2.6.

Левой (правой) полуокрестностью точки x₀ называется полуоткрытый промежуток вида 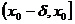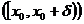, где δ - положительное число.

Определение 2.7.

Пусть функция f(x) определена в некоторой левой полуокрестности точки x₀ за исключением возможно самой точки x₀. Число а называется левосторонним пределом функции f(x) в точке x₀, если для любого положительного числа 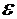существует положительное число 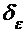такое, что 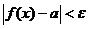, если .

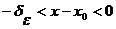Обозначение: .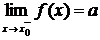

Аналогично определяется правосторонний предел функции f(x) в точке x₀.

Обозначение: .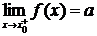

Теорема 2.1.

Для существования предела 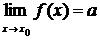необходимо и достаточно существования и равенства односторонних пределов: =

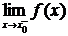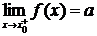
Пример 2.5.

Рассмотрим функцию sn(x)= 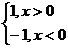(см. пример 1.8.)

Имеем , .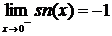

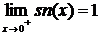По теореме 2.1 не существует предела функции sn(x) в точке x₀ = 0.

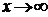2.3. Предел функции при . Бесконечно малые и бесконечно большие функции.

Определение 2.8.

Пусть функция f(x) определена на некотором множестве 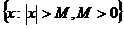, то есть определенa при достаточно больших по модулю значениях x. Число а называется пределом функции f(x) при 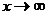, если для любого положительного числа 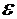существует положительное число 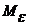такое, что 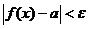, если .

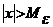Обозначение: .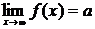

Замечание 2.2.

Если x стремится к бесконечности, принимая лишь положительные (отрицательные) значения, то соответствующий предел обозначается символом .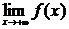

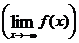Замечание 2.3.

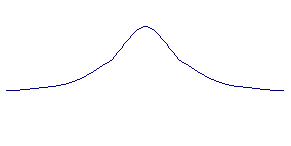
С геометрической точки зрения равенство 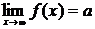означает, что график функции f(x) неограниченно приближается к горизонтальной прямой y=a.

Пример 2.6.

Доказать, что .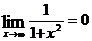

Решение

Рассмотрим произвольное положительное число 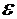. Неравенство

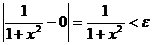равносильно неравенству .

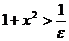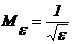Положим , тогда если 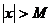, то 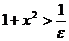, а значит, .

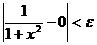Таким образом, .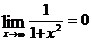

Схематичный график функции 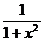представлен на рисунке 2.2.

рис. 2.2.

у

х

О

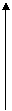
Определение 2.9.

Функция f(x) называется бесконечно малой функцией при , если .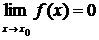

Определение 2.10.

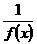Функция f(x) называется бесконечно большой функцией при , если функция есть бесконечно малая функция при .

Обозначение: .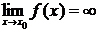

Замечание 2.4.

В том случае, когда f(x) принимает только положительные (отрицательные) значения при всех х, близких к точке , ( ).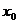

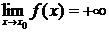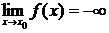Пример 2.7.

Функция 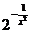является бесконечно малой функцией при х 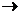0 ( 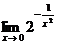=0), а функция 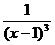- бесконечно большой функцией при х → 1( ).

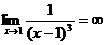Теорема 2.2. (о свойствах бесконечно малых и бесконечно больших функций).

1. Произведение бесконечно малой (большой) при функции на постоянную, отличную от нуля, есть бесконечно малая (большая) при функция.

2. Произведение двух бесконечно малых (больших) при функций есть функция бесконечно малая (большая) при .

3. Сумма двух бесконечно малых при функций есть бесконечно малая при функция.

Замечание 2.5.

Свойство 3 для бесконечно больших функций вообще говоря не выполняется.