Тема 5 Случайные события. Вероятность события

Наблюдение явления (эксперимент) называется испытанием. Результат испытания называется событием.

Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

Два события называются несовместными, если появление одного из них исключает появления другого в одном и том же испытании.

Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит.

Событие, противоположное событию 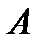, обозначают через .

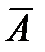Событие называют достоверным, если в данном испытании оно является единственно возможным.

Событие называют невозможным, если в данном испытании оно заведомо не может произойти.

Событие называют случайным, если оно объективно может наступить или не наступить в данном испытании.

Совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится одно из них.

Событие 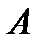называется благоприятствующим событию 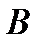, если наступление события 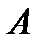влечет за собой наступление события .

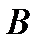Классическое определение вероятности. Вероятностью 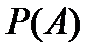события 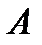называют отношение 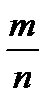числа исходов, благоприятствующих событию 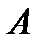, к общему числу исходов, т.е.

.

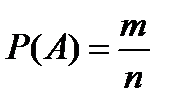Свойства вероятности

1. Вероятность достоверного события равна единице: .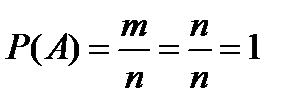

2. Вероятность невозможного события равна нулю: .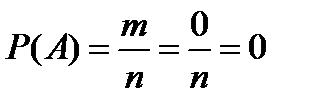

3. Вероятность случайного события есть число, заключенное между нулем и единицей:

.

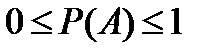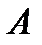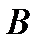Суммой событий и называется событие 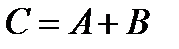, состоящее в том, что произошло или событие 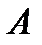, или событие 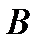, или оба одновременно.

Произведением событи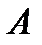й и 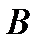называют событие 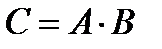, состоящее в том, что произошло и событие 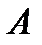, и событие .

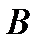Теорема сложения вероятностей несовместных событий. Вероятность наступления одного из несовместных событий равна сумме вероятностей этих событий:

.

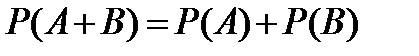Следствие.Сумма вероятностей противоположных событий равна единице:

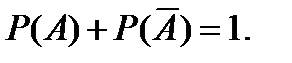
Два события 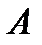и 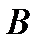называют независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события называют зависимыми.

Условной вероятностью 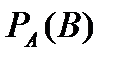события 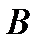называют вероятность события 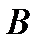, вычисленную в предположении, что событие 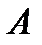уже наступило.

Заметим, что если события 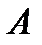и 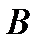независимы, то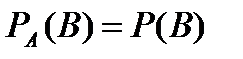

Теорема умножения вероятностей.

1. Вероятность произведения двух зависимых событи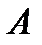й и 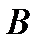равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое уже наступило:

.

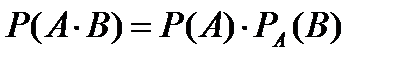2. Вероятность произведения двух независимых событи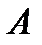й и 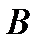равна произведению вероятностей этих событий:

.

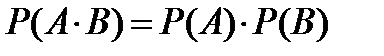Теорема сложения вероятностей совместных событий. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения:

.

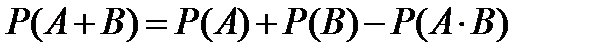Формула полной вероятности. Вероятность события 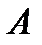, которое может наступить лишь при условии появления одного из 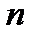попарно несовместных событий 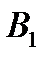, , 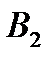…, 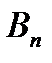(их называют гипотезами), образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события :

.

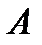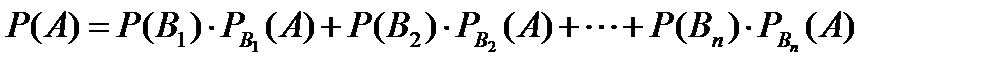Формула Бейеса. Если произведено одно испытание, в результате которого произошло событие 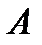, то можно переоценить вероятности гипотез:

( ),

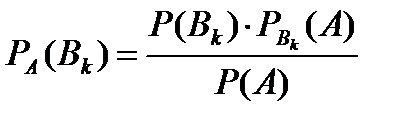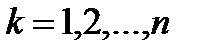где вероятность 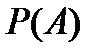вычисляется по формуле полной вероятности.