Достаточное условие абсолютной сходимости знакопеременного ряда.

Рассмотрим знакопеременный ряд 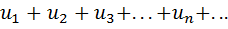(1)

Пусть сходиться знакоположительныйряд составленный из модулей членов ряда (1), тогда ряд (1) также сходиться.

(такая сходимость одновременно с знакоположительным рядом из модулей называется абсолютной). Следовательно ряд (1) сходится абсолютно.

Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходиться.

Знакопеременный ряд называется условно сходящимся, если сам он сходиться, а ряд, составленный из модулей его членов, расходиться

10. Функциональные ряды. Область сходимости…

Рассмотрим функциональный ряд:

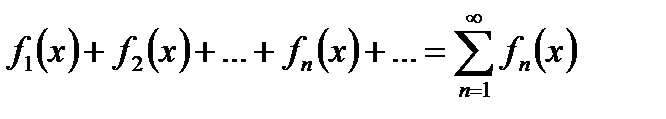(1)

где 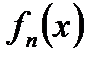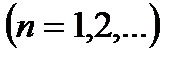- функции, определенные на некотором множестве А. Придавая х определенные числовые значения, получаем различные числовые ряды, которые могут оказаться сходящимися или расходящимися.

Совокупность значений х, при которых функциональный ряд (1) сходится, называют областью сходимости ряда.

Функциональный ряд (1) называется мажорируемым на [a, в] если существует такой сходящийся числовой ряд 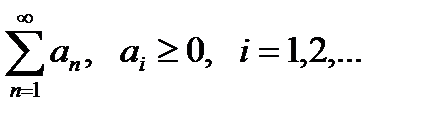, что для всех 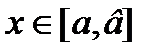выполняются: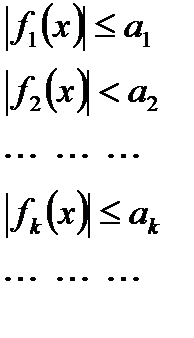

15. Интервал сходимости степенного ряда. Степенным рядом называется выражение: 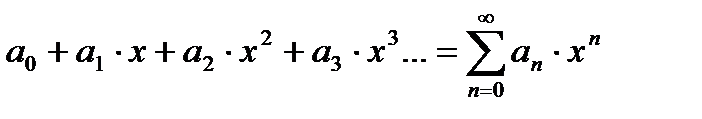(1)

Те значения х при которых ряд (1) сходится называются областью сходимости степенного ряда.

Теорема Абеля.

1) Если степенной ряд (1) сходится при некотором значении 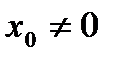, то он сходится абсолютно при любом значении .

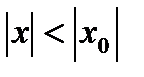2) Если ряд (1) расходится при некотором значении 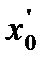, то он расходится при любом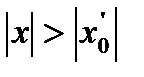

16 Вывод формулы радиуса:

Для этого рассмотрим абсолютный ряд 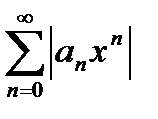. Для каждого фиксированного х применим к абсолютному ряду признак Даламбера: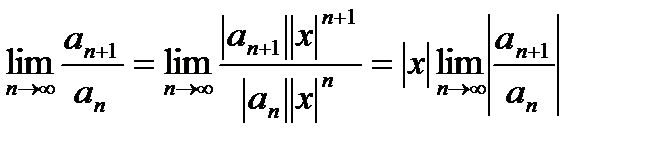

Пусть 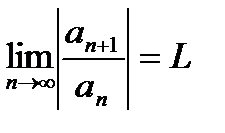. Тогда по признаку Даламбера абсолютный ряд сходится, если 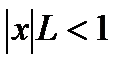, и расходится при 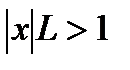. Следовательно исходный ряд сходится абсолютно при 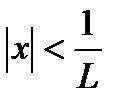и расходится при 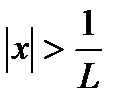. Т. о. число L является радиусом сходимости, т. е.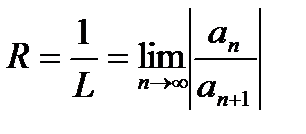

17. Свойства степенных рядов. Абсолютная сходимость, интегрируемость и дифференцируемость.

Свойства:

1) Сумма 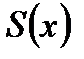степенного ряда 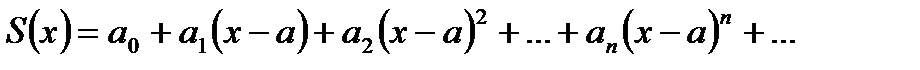(1) является непрерывной функцией в каждой точке интервала сходимости .

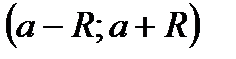2) Ряд 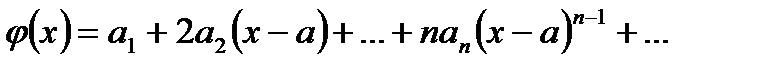(2) полученный почленным дифференцированием ряда (1), является степенным рядом с тем же, что и ряд (1), интервалом сходимости 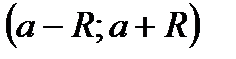. Сумма ряда (2) .

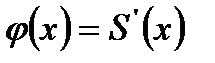3) Пусть числа 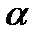и 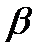принадлежат интервалу сходимости 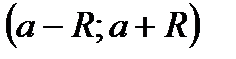ряда (1). Тогда имеет место равенство: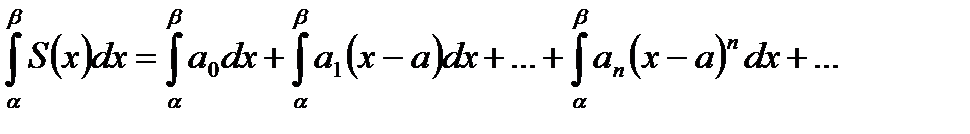

Теорема Абеля.

3) Если степенной ряд (1) сходится при некотором значении 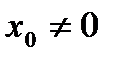, то он сходится абсолютно при любом значении .

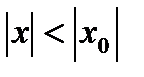4) Если ряд (1) расходится при некотором значении 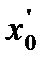, то он расходится при любом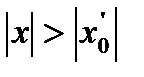

18. Ряд Тейлора и Маклорена.

Если функция 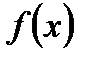имеет производные любого порядка в окрестности точки 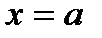, то получим бесконечный ряд, который называется рядом Тейлора: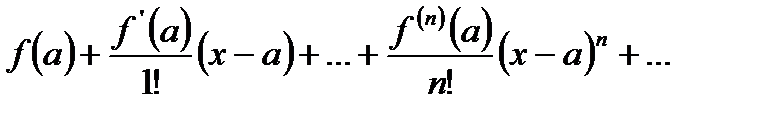

При 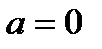получим частный случай ряда Тейлора, который называют рядом Маклорена:

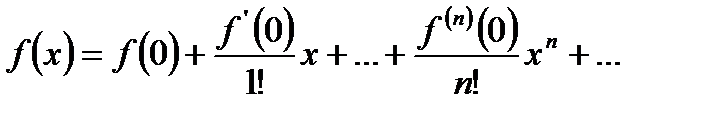
36. Производная функции компл. переменной. Условия Коши-Римана.

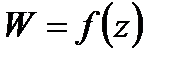называется функцией комплексного переменного если одному допустимому значению z поставлено в соответствие одно, несколько или бесконечное множество значений W.

Определение.

Пусть 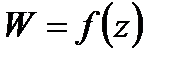- функция комплексной переменной, определенная в 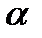-окрестности точки 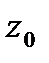, и существует предел 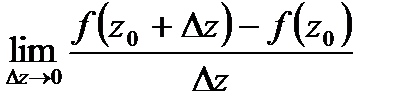(1)

Тогда этот предел называется производной функции 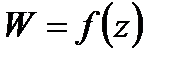в точке 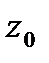; при этом функция 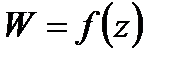называется дифференцируемой в точке .

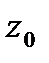Условия Коши-Римана.

Пусть у функции 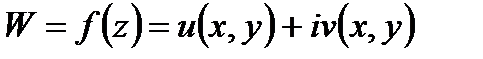вещественная и мнимая части дифференцируемы как функции двух переменных, тогда, для того, чтобы эта функция была дифференцируема как функция комплексного переменного необходимо и достаточно выполнение условий: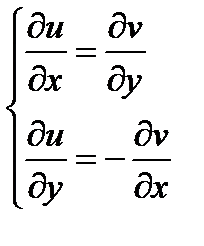

24)Разложение периодической функции с периодом L.

Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.

Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид

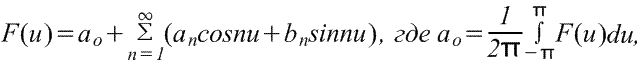
25)Четные и нечетные функции.

Л.1: Если 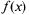— четная функция на 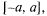то

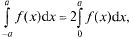если 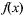— нечетная функция на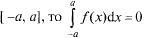

Для четных функций

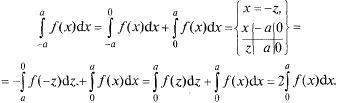
Для нечетной функции доказательство аналогично Л.2: Произведение двух четных или двух нечетных функций есть четная функция, четной и нечетной — нечетная функция - четные функции

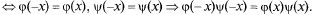
Остальное доказывается аналогично

С помощью лемм 1, 2 получаем следующие коэффициенты Фурье:

— для четной функции:

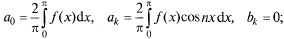
— для нечетной функции:

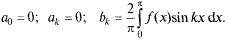
Таким образом, ряд Фурье для четной функции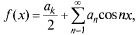

для нечетной функции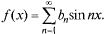

.