Необходимы признак сходимости.

Необходимы признак сходимости.

Если ряд сходится, то его n-ый член стремится к 0 при неограниченном возрастании n (обратное утверждение неверно).

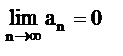- необходимый признак (условие) сходимости ряда.

Если 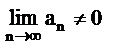то ряд расходящийся – достаточное условие расходимости ряда.

Признаки сравнения знакоположительных рядов.

Первый признак сравнения.

Пусть даны два знакопол. ряда а₁+а₂+а₃+…+а_n+…= 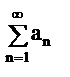(1) и b₁+b₂+b₃+…+b_n+…= 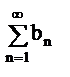(2).

Если члены ряда (1) не больше соответствующих членов ряда (2), т.е. а_n b_n и ряд (2) сходится, то и ряд (1) также сходится.

Если члены ряда (1) не меньше соответствующих членов ряда (2), т.е. а_n 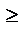b_n и ряд (2) расходится, то и ряд (1) также расходится.

Этот признак сравнения справедлив, если неравенство выполняется не для всех n, а лишь начиная с некоторого.

Второй признак сравнения.

Если сущ. конечный и отличный от 0 предел 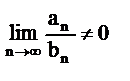, то оба ряда сход.или расх. одноврем.

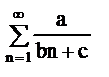-ряды такого вида расх. по второму призн. сравнения. Их надо сравн с гармонич.рядом.

Признак Даламбера.

Если для знакоположительного ряда (а₁+а₂+а₃+…+а_n+…= 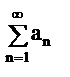) существует 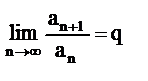(1), то ряд сходится, если q<1, расходится, если q>1. Если q=1 то вопрос остается открытым.

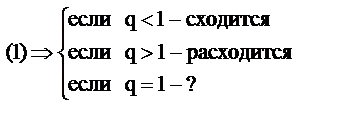
Признак Коши (радикальный).

Если для знакоположительного ряда существует предел 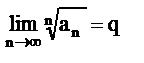(2), то ряд сходится, если q<1, расходится, если q>1. Если q=1 то вопрос остается открытым.

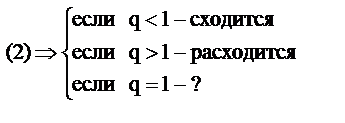
7. Интегральный признак Коши. Исследование сходимости ряда .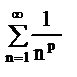

Если существует предел 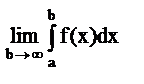. Это есть несобственный интеграл и обозначается .

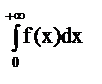Если этот предел конечен, то говорят, что несобственный интеграл сходится. Ряд, соответственно, сходится или расходится.

Пусть ряд а₁+а₂+а₃+…+а_n+…= 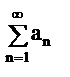- знакоположительный ряд.

Обозначим a_n=f(x) и рассмотрим функцию f(x). Если f(x)- функция положительная, монотонно убывающая и непрерывная, то, если несобственный интеграл сходится, то и данный ряд сходится. И наоборот: если несобственный интеграл расходится, то и ряд расходится.

Если ряд конечен, то он сходится.

Очень часто встречаются ряды 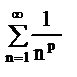- ряд Дерихле. Он сходится, если p>1, расходится p<1. Гармонический ряд является рядом Дерихле при р=1. Сходимость и расходимость данного ряда легко доказать с помощью интегрального признака Коши.

8. Знакопеременные ряды. Условная и абсолютная сходимость.

Ряд называется знакопеременным, если он имеет бесконечное число как положительных, так и отрицательных членов.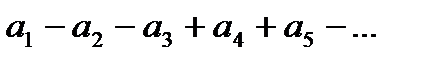

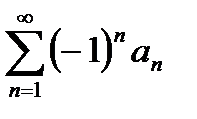(1)

Знакочередующийся ряд (1) называется сходящимся абсолютно если сходится ряд составленный из абсолютных величин его членов. Если ряд (1) сходится, а ряд составленный из абсолютных величин расходится, то говорят что этот ряд сходится условно.

. Признак Лейбница.

Пусть для знакочередующегося ряда 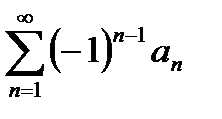выполнены условия:

1) последовательность 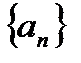является невозрастающей, т. е. ;

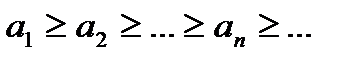2)

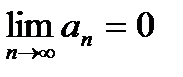
Тогда ряд 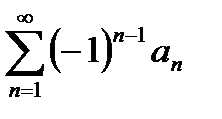сходится.

Теорема Лейбница позволяет оценить количество слогаемых знакочередующегося ряда, которые нужно сложить чтобы получить его сумму с заданной точностью.

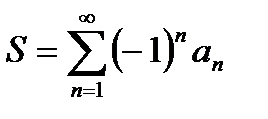- сходится,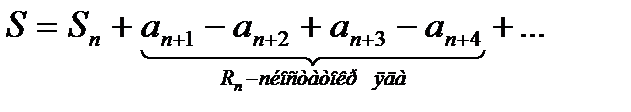

Элементы теории поля

Скалярное поле

Определения

Скалярное поле определяется скалярной функцией точки 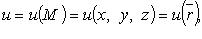где 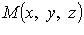- точка пространства, 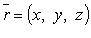- ее радиус-вектор.

Градиент

Свойства градиента

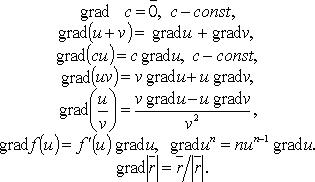
Векторное поле Определение Векторное поле определяется векторной функцией точки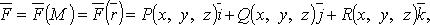

где 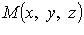- точка пространства, 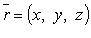- ее радиус-вектор.

Формула Остроградского

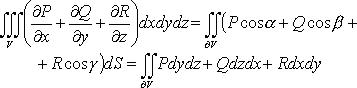
Необходимы признак сходимости.

Если ряд сходится, то его n-ый член стремится к 0 при неограниченном возрастании n (обратное утверждение неверно).

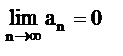- необходимый признак (условие) сходимости ряда.

Если 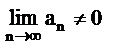то ряд расходящийся – достаточное условие расходимости ряда.