Таким образом, уравнение искомой прямой имеет вид

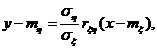
и называется прямой среднеквадратической регрессии ηнаξ

- коэффициент регрессии ηнаξ.

При этом ошибка замены равна:

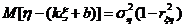
Аналогично можно получить прямую среднеквадратической регрессии ξ на η:

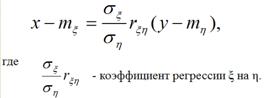
Уравнения регрессии

Т.к. М[ξ | η = y] меняется с изменением значения у, то можно рассматривать функцию

m_ξ(y)=М[ξ | η=y],

Аналогично можно рассматривать и функцию

m_η(x)=M[η | ξ=x].

Эти функции называются соответственно регрессиями ξпоη и η по ξ.

Уравнения х = m_ξ(y) и у = m_η(x) называются уравнениями регрессии, а линии, определяемые этими уравнениями, называются линиями регрессии.

36)Доказательства неравенств Чебышёва

Первое неравенство Чебышева. Пусть Х – неотрицательная случайная величина (т.е. 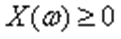для любого ). Тогда для любого положительного числа асправедливо неравенство

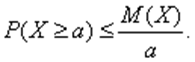
Доказательство. Все слагаемые в правой части формулы (4), определяющей математическое ожидание, в рассматриваемом случае неотрицательны. Поэтому при отбрасывании некоторых слагаемых сумма не увеличивается. Оставим в сумме только те члены, для которых . Получим, что

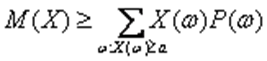. (9)

Для всех слагаемых в правой части (9) 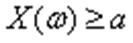, поэтому

. (10)

Из (9) и (10) следует требуемое.

Второе неравенство Чебышева. Пусть Х – случайная величина. Для любого положительного числа а справедливо неравенство

.

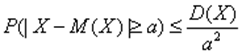Это неравенство содержалось в работе П.Л.Чебышёва «О средних величинах», доложенной Российской академии наук 17 декабря 1866 г. и опубликованной в следующем году.

Для доказательства второго неравенства Чебышёва рассмотрим случайную величину У = (Х – М(Х))². Она неотрицательна, и потому для любого положительного числа b, как следует из первого неравенства Чебышёва, справедливо неравенство

.

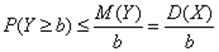Положим b = a². Событие {Y>b} совпадает с событием {|X – M(X)|>a}, а потому

,

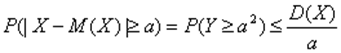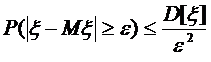что и требовалось доказать.

Сходимость по вероятности, теорема Чебышёва, центральная предельная теорема.

Если ξ₁, ξ₂, …, ξ_n, … независимы и существует константа C>0, что Dξ_n ≤ Cдля всехn, то при любом ε

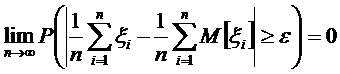
Таким образом среднее арифметическое случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий

Центральная предельная теорема для одинаково распределенных случайных величин.

Если случайные величины ξ₁, ξ₂, …, ξ_n, … независимы, одинаково распределены и имеют конечные Mξ_n=a и Dξ_n =σ²> 0, то

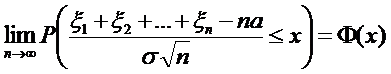
Центральная предельная теорема (теорема Ляпунова)

Пусть случайные величины ξ₁, ξ₂, …, ξ_n, … независимы. Обозначим . Если все a_i,

σ_i, m_iконечны и , то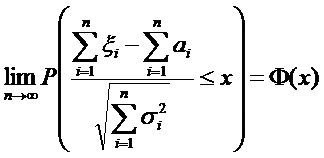

Анализ выборки: вариационный ряд, полигон, гистограмма, эмпирический закон и функция распределения.

Виды выборок

Повторная выборка – отобранный объект после обследования возвращается в совокупность перед отбором следующего объекта.

Бесповторная выборка – отобранный объект не возвращается в совокупность при обследовании.

(На практике обычно пользуются бесповторными выборками)

Репрезентативная (представительная) – дает правильное представление о совокупности,

(насколько это позволяют имеющиеся деньги и время)

Ошибочно сформированная выборка даст искаженное представление о совокупности.

В силу закона больших чисел можно утверждать, что выборка будет представительной,

· если ее объем достаточно велик, а ее значения независимы;

· если ее осуществлять случайно и если все ее объекты имеют одинаковую вероятность попасть в выборку.

(Если объем совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторными и бесповторными выборками практически исчезает)