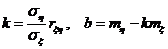Числовые характеристики двумерной случайной величины: моменты, ковариация, коэффициент корреляции. Свойства (теоремы) для математического ожидания и дисперсии.

Числовые характеристики двумерной случайной величины

Начальным моментом порядка k+s случайной величины (ξ,η) называется

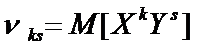
Согласно определению математического ожидания

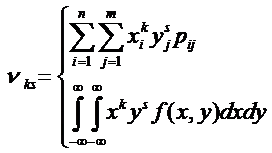
Центральным моментом порядка k+s случайной величины (ξ,η) называется

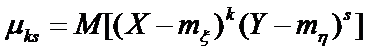
Например,

n₁₀=M[ξ¹×η⁰]=m_ξ, n₀₁=M[ξ⁰ ×η¹]=m_η,

m₁₀=M[ξ – m_ξ]=0, m₀₁=M[η – m_η]=0,

m₂₀=M[(ξ – m_ξ)²]=D_ξ, m₀₂=M[(η – m_η)²]=D_η,

m₁₁=M[(ξ – m_ξ)(η – m_η)]=k_ξη называется моментом корреляции (иначе моментом связи) или ковариацией случайных величин ξ и η.

Для ковариации справедлива формула:

k_ξη =M[(ξ – m_ξ)(η – m_η)]=M[ξη] – m_ξ m_η.

Коэффициентом корреляции назовем

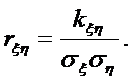
Случайные величины ξ и η, для которых k_ξη = 0 (а значит и r_ξη =0), называются некоррелированными (несвязанными).

Если k_ξη ¹ 0 (а значит и r_ξη ¹0), то ξ и η называются коррелированными (это есть признак наличия зависимости между ними).

Можно доказать, что если ξ и η независимые случайные величины, то k_ξη =0 (а значит и r_ξη =0),

т.е. ξ и η некоррелированные величины

Заметим, что из некоррелированности случайных величин, в общем случае, еще не следует их независимость. Можно построить примеры таких случайных величин, которые являются некоррелированными, но зависимыми.

Итак:

· из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность.

· Из независимости двух величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.

· Числа k_ξη и r_ξη характеризуют не всякую зависимость, а только так называемую линейную зависимость между случайными величинами ξ и η. Некоррелированность эквивалентна линейной независимости.

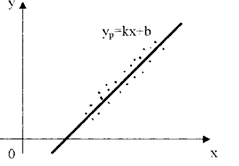
Найдем линейную зависимость у=kx+b , которая давала бы возможность предсказывать как можно точнее значения случайной величины η по значениям случайной величины ξ, т.е. такую линейную зависимость, чтобы ошибка предсказания M[(η-y)²], была минимальной.

В этом случае

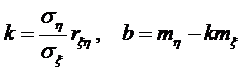
Таким образом, уравнение искомой прямой имеет вид

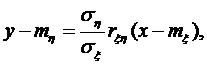
и называется прямой среднеквадратической регрессии ηнаξ

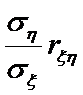- коэффициент регрессии ηнаξ.

При этом ошибка замены равна:

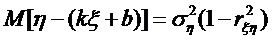
Аналогично можно получить прямую среднеквадратической регрессии ξ на η:

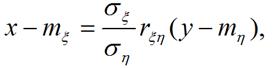
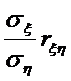- коэффициент регрессии ξнаη.

1. Основные теоремы о математических ожиданиях и дисперсиях

Теорема. M[ξη]= m_ξ m_η + k_ξη

Следствие. Если ξ и η независимые случайные величины, то M[ξη]= m_ξ m_η

Теорема. D[ξ+η]=D[ξ]+D[η] + 2k_ξη

Следствие. Если ξ и η - независимые случайные величины, то D[ξ+η]=D[ξ]+D[η].

Вывод уравнения среднеквадратической регрессии.

Числа k_ξη и r_ξη характеризуют не всякую зависимость, а только так называемую линейную зависимость между случайными величинами ξ и η. Некоррелированность эквивалентна линейной независимости.

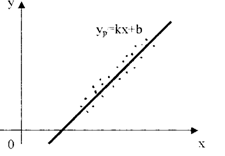
Найдем линейную зависимость у=kx+b , которая давала бы возможность предсказывать как можно точнее значения случайной величины η по значениям случайной величины ξ, т.е. такую линейную зависимость, чтобы ошибка предсказания M[(η-y)²], была минимальной.

В этом случае