Нормальное непрерывное распределение, функция распределения и плотность, математическое ожидание и дисперсия, вероятность попадания в интервал, правило трех сигм.
Нормальное распределение
Непрерывная случайная величина ξ имеет нормальное распределение, если плотность вероятности
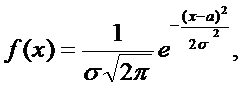
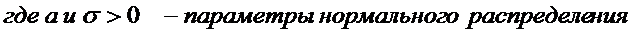
Нормальное распределение с параметрами a =0 и s=1 называется стандартным (основным), плотность вероятности в этом случае обозначается j(х)
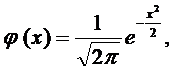
Нормальное распределение является предельным законом, к которому приближаются другие законы распределения. Мы рассмотрим позднее центральную предельную теорему теории вероятностей, утверждающую, что при достаточно большом n сумма независимых случайных величин ξ1, ξ2,..., ξn, подчиненным каким угодно законам распределения (при соблюдении некоторых ограничений), будет иметь закон распределения, как угодно близкий к закону нормального распределения.
Числовые характеристики нормального распределения
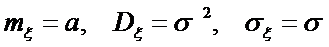
Таким образом, параметр aявляется математическим ожиданием, а параметр s - средним квадратическим отклонением случайной величины, имеющей нормальное распределение.
График плотности вероятности - кривая Гаусса (нормальная кривая).
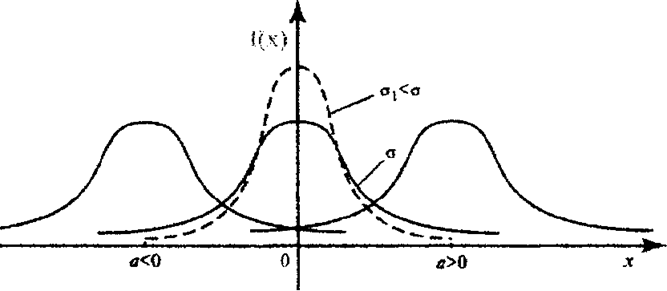
Кривая Гаусса симметрична относительно прямой х = а и имеет максимум при х = а, равный
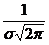
ветви кривой асимптотически приближаются к оси Ox.
Для нормально распределенной случайной величины функция распределения имеет вид
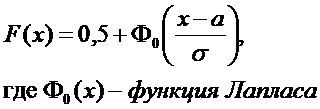
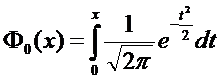
Ф0(х) - функция нечетная, т.е. Ф0 (-х)= - Ф0 (х) и она затабулирована.
Замечание .
Для того чтобы стандартизировать случайную величину, надо вычесть из нее математическое ожидание и поделить на среднее квадратическое отклонение:
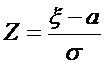
Вероятность попадания в интервал
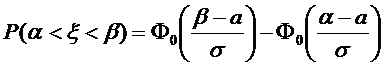
Следствие:
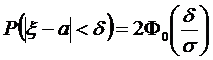
Нахождение доверительного интервала
Если задана доверительная вероятность р, то
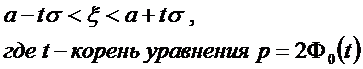
Правило трех сигм
Если заданаt = 3, то
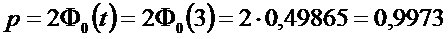
Итак,
P(а-3s<ξ<а+3s)=0,9973,
т.е. практически все значения случайной величины находятся в интервале (а-3s; а+3s). Вероятность же того, что значения случайной величины попадут вне этого интервала пренебрежимо мала и равна 0,0027.
Пример . Ошибка измерения подчинена нормальному закону с параметрами а =5м, s=10м. Найти вероятность того, что измеренное значение расстояния будет отклоняться от истинного не более, чем на 15м.
Решение.
Случайная величина ξ-ошибка измерения,
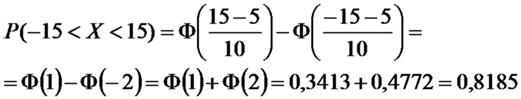
3Пример . На станке изготовляются втулки, длина которых L представляет нормально распределенную случайную величину, причем М[L] = 20cм, s = 0,2 см.
Найти:
· Вероятность того, что длина втулки будет отклоняться от ее среднего значения на величину, меньшую 0,3см.
· Длину втулки с вероятностью 0,95.
· Длину втулки с вероятностью 0,9973.
Решение.
• По условию а=20см, s=0,2 см.
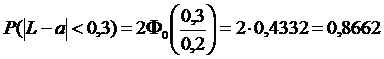
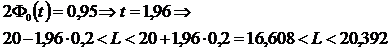
• так как по условию р = 0,9973, то
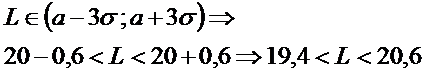
Функция случайного аргумента. Закон распределения для дискретной случайной величины, вывод формулы для плотности непрерывной случайной величины.
