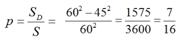Вероятностным пространством называется тройка

(W, S, P), где

W – универсальноемножество

S – егоσ-алгебра

P – функция из S в множество действительных чисел, удовлетворяющая свойствам

1) P(A) ≥ 0; Всякому событию из поля события ставят в соответствие некоторое неотрицательное число, которое называют его вероятностью

2) P(W) = 1; Вероятность достоверного события принимается равной единице

3) Если A₁, A₂, …A_n, … не пересекаются, то

P(A₁ +A₂+ …+A_n+ …) = P(A₁) + P(A₂) + …+P(A_n)+ … (аксиома сложения).
Вероятность суммы двух несовместных событий равна сумме вероятностей каждого

Аксиома 4. Если событие А равносильно наступлению хотя бы одного из попарно несовместных событий А1, А2, …,Аn , то вероятность этого события равна сумме вероятностей каждого .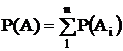

Следствия:
1. Вероятность противоположного события равна 1 за вычетом вероятности прямого события
;
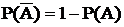Доказательство ;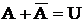
.
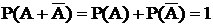2. Вероятность невозможных событий равна 0

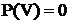
Доказательство
.
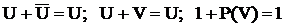3. Вероятность любого события лежит в пределах

0 <= Р(Аi) <= 1.

2. Классическая и геометрическая вероятности. Определение (интерпретация аксиом), примеры.

Классическая вероятность

Пространство W состоит из конечного числа равновероятных элементарных событий Е₁, Е₂,...,Е_n.

Элементарное событие называется благоприятным событию А, если его появление влечет появление события А. Пусть m - число благоприятных для А элементарных событий, n - число всех элементарных событий. Тогда

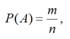
Действительно, Р(Е₁+Е₂+...+Е_n)=Р(W)=1, так как события несовместны, то

Р(Е₁) + Р(Е₂) +...+ Р(Е_n) =1 (1).

По условию события равновозможные, следовательно,

Р(Е₁) = Р(Е₂) =...= Р(Е_n) (2).

Из равенств (1) и (2) следует, что Р(Е₁)=Р(Е₂) =…

=Р(Е_n) =

Найдем

Р(А) = Р(Е₁ + Е₂ +... + Е_m) = Р(Е₁)+Р(Е₂)+...+Р(Е_m) =m/n

Пример:

Опыт - бросание игральной кости

Событие А - выпадение числа очков, кратного 3.

Найдем вероятность события А.

Решение:

Всего случаев 6. Благоприятных из них 2, следовательно,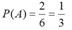

Геометрическая вероятность

Пространство W является ограниченной и измеримой областью в Rⁿ. Сигма-алгебра пространства есть совокупность всех измеримых подмножеств области W.

Вероятность события А (вероятность попадания точки в множество А) пропорциональна его мере как множества

и не зависит от его расположения и формы.

Если мера всей области равна S, а мера части D области, попадание в которую благоприятствует появлению события А, равна S_D, то вероятность события А равна.

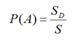
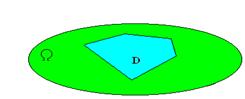
Геометрическая вероятность

На практике часто встречаются испытания, число возможных исходов которых бесконечно.

Два студента условились встретиться в определенном месте между 18 и 19 часами. Пришедший первым ждет 15 мин и уходит. Определить вероятность встречи, если время прихода каждого независимо и равновозможно в течение указанного часа.

Решение примера 6:

Пусть х- время прихода одного студента, у- время прихода второго. Чтобы встреча состоялась, необходимо и достаточно, чтобы êх - у ê£ 15,

т.е. -15 £ x - y £ 15. Область возможных значений - квадрат со стороной, равной 60. 4

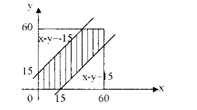
Область D – часть квадрата между прямыми

х – у = – 15 и х – у = 15. Следовательно,