Функция, заданная параметрически
Будем говорить, что переменная y как функция аргумента x задана параметрически, если обе переменные x и y заданы как функции 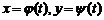 некоторой третьей переменной t, называемой параметром.
некоторой третьей переменной t, называемой параметром.
Параметрические уравнения играют важную роль, например, в механике, где координаты 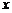 и
и 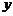 движущейся точки рассматриваются как функции времени.
движущейся точки рассматриваются как функции времени.
Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений
 |
где t — вспомогательная переменная, называемая параметром.
Найдем производную у'х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции

Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'х=y't•t'x. С учетом равенства (21.2) получаем
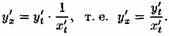
Полученная формула позволяет находить производную у'х от функции заданной параметрически, не находя непосредственной зависимости у от х.
442. Производные и дифференциалы высших порядков.
Пусть функция 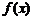 имеет производную в каждой точке
имеет производную в каждой точке 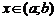 . Тогда на промежутке
. Тогда на промежутке 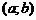 будет определена функция
будет определена функция 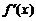 , и можно говорить о производной этой функции.
, и можно говорить о производной этой функции.
Производной второго порядка функции 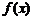 называется производная от производной первого порядка
называется производная от производной первого порядка 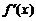 , если она существует, и обозначается
, если она существует, и обозначается 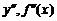 .
.
Производную от второй производной называют производной третьего порядка и обозначают 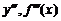 .
.
Аналогично производная n-го порядка является производной от производной 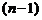 -го порядка и обозначается
-го порядка и обозначается 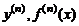 .
.
Производные высших порядков широко применяются, в частности, в физике. Выясним, например, физический смысл второй производной.
Пусть материальная точка движется прямолинейно и пройденный ею путь описывается уравнением 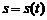 , t – время. Как известно из § 1, первая производная от пути по времени есть мгновенная скорость движения точки в момент времени
, t – время. Как известно из § 1, первая производная от пути по времени есть мгновенная скорость движения точки в момент времени 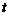 :
: 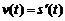 . Тогда вторая производная от пути по времени
. Тогда вторая производная от пути по времени 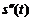 равна скорости изменения функции скорости
равна скорости изменения функции скорости 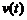 . А это есть ускорение a(t) материальной точки в момент времени t. Таким образом, вторая производная от пути по времени есть ускорение, т.е.
. А это есть ускорение a(t) материальной точки в момент времени t. Таким образом, вторая производная от пути по времени есть ускорение, т.е. 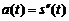 .
.
Найдем производные n-го порядка для некоторых элементарных функций.
1) Найдем 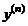 степенной функции
степенной функции 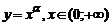 ,
, 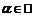 . Очевидно,
. Очевидно, 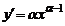 ,
, 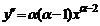 ,…,
,…, 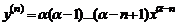 .
.
Если предположить, что 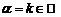 , то
, то
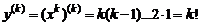 ,
, 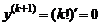 .
.
2) Замечательным свойством обладает показательная функция 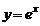 . Для любого n справедлива формула
. Для любого n справедлива формула
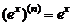 .
.
3) Найдем n-ую производную функции 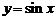 . Будем иметь
. Будем иметь
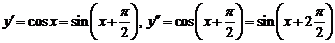 ,
,
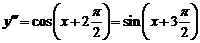 .
.
Можно показать, что
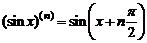 . (1)
. (1)
4) Аналогично,
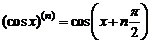 . (2)
. (2)
Дифференциалы высших порядков
Пусть функция 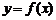 дифференцируема на некотором интервале
дифференцируема на некотором интервале 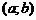 . Дифференциал этой функции
. Дифференциал этой функции 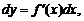 который также называется ее первым дифференциалом, зависит от двух переменных
который также называется ее первым дифференциалом, зависит от двух переменных 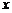 и
и 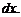
Пусть функция 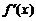 , в свою очередь, дифференцируема в некоторой точке
, в свою очередь, дифференцируема в некоторой точке 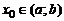 . Тогда дифференциал в этой точке функции
. Тогда дифференциал в этой точке функции 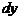 , рассматриваемой как функция только от
, рассматриваемой как функция только от 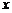 (т.е. при некотором фиксированном
(т.е. при некотором фиксированном 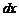 ), если для его обозначения использовать символ
), если для его обозначения использовать символ 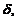 имеет вид
имеет вид
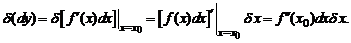
Значение дифференциала 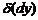 , т.е. дифференциала от первого дифференциала, в некоторой точке
, т.е. дифференциала от первого дифференциала, в некоторой точке 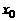 при
при 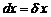 называется вторым дифференциалом функции
называется вторым дифференциалом функции 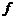 в этой точке и обозначается через
в этой точке и обозначается через 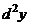 , т.е.
, т.е.
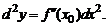 (1)
(1)
При записи степени дифференциала аргумента принято опускать скобки (в частности, вместо 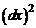 будем писать
будем писать 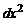 ).
).
Подобным же образом, в том случае, когда производная 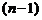 -го порядка
-го порядка 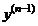 дифференцируема в точке
дифференцируема в точке 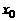 , определяется дифференциал
, определяется дифференциал 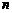 -го порядка
-го порядка 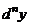 функции
функции 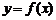 в точке
в точке 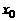 как дифференциал
как дифференциал 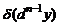 от дифференциала
от дифференциала 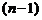 -го порядка
-го порядка 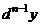 , в котором
, в котором 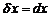 :
:
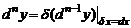 .
.
Имеет место формула:
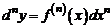 . (2)
. (2)
Отсюда получаем другую запись для n-ой производной:
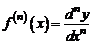 . (3)
. (3)
45. Дифференциал функции и его геометрический смысл. Применение дифференциала в приближённых вычислениях. Инвариантность формы первого дифференциала. Непрерывность дифференцируемой функции.
451. Дифференциал функции и его геометрический смысл.
Дифференциал функции. Пусть функция 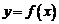 дифференцируема в точке
дифференцируема в точке 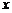 . Тогда приращение функции в этой точке может быть записано по формуле (1), где
. Тогда приращение функции в этой точке может быть записано по формуле (1), где 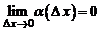 . Так как
. Так как 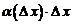 является бесконечно малой функцией более высокого порядка по сравнению c
является бесконечно малой функцией более высокого порядка по сравнению c 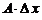 (при условии, что
(при условии, что 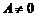 ), то
), то 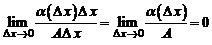 . Поэтому первое слагаемое
. Поэтому первое слагаемое 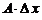 является главной частью приращения
является главной частью приращения 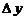 , линейной относительно
, линейной относительно 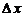 .
.
Главная часть приращения функции 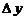 в точке x, линейная относительно
в точке x, линейная относительно 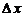 , называется дифференциалом функции
, называется дифференциалом функции 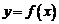 в этой точке. Для обозначения дифференциала используется обозначение
в этой точке. Для обозначения дифференциала используется обозначение 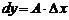 , а поскольку
, а поскольку 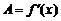 , то
, то
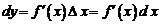 . (2)
. (2)
Если 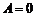 , то
, то 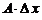 не является, вообще говоря, главной частью приращения
не является, вообще говоря, главной частью приращения 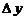 . В этом случае, по определениюполагают
. В этом случае, по определениюполагают 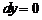 .
.
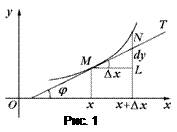
Геометрический смысл дифференциала. Для выяснения геометрического смысла дифференциала проведем к графику функции 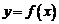 в точке
в точке 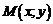 касательную МТ (рис.1) и обозначим через
касательную МТ (рис.1) и обозначим через 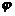 угол ее наклона к положительному направлению оси
угол ее наклона к положительному направлению оси 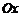 .
.
 Поскольку
Поскольку 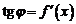 , то
, то 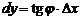 . Поэтому из треугольника MLN следует, что дифференциал dy есть приращение ординаты точки касания, соответствующее приращению аргумента
. Поэтому из треугольника MLN следует, что дифференциал dy есть приращение ординаты точки касания, соответствующее приращению аргумента 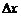 .
.
Из обозначения производной функции 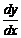 или
или 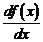 видно, что производная функции
видно, что производная функции 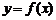 равна отношению дифференциала этой функции к дифференциалу аргумента.
равна отношению дифференциала этой функции к дифференциалу аргумента.
452. Применение дифференциала в приближённых вычислениях.
Пусть имеет место формула (1.1). Перейдем от нее к приближенной формуле 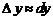 или
или 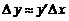 . Тогда
. Тогда 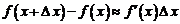 , откуда
, откуда
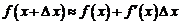 . (1)
. (1)
Формула (1) позволяет вычислить приближенное значение функции, соответствующее приращенному значению аргумента, если известно ее значение в некоторой точке и значение производной в этой точке, когда приращение аргумента является достаточно малым.
453. Инвариантность формы первого дифференциала.
Форма записи дифференциала не зависит от того, является аргумент независимой переменной или функцией другого аргумента. Это свойство дифференциала называют инвариантностью формы дифференциала.
454. Непрерывность дифференцируемой функции.
Теорема 1. Пусть функцияy = f(x) дифференцируема на интервале (a, b). Тогда функция fнепрерывна на (a, b).
Доказательство
Возьмем произвольное фиксированное число x  (a,b).
(a,b).
По условию теоремы
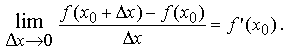
Следовательно, в малой окрестности числа x0 можно определить функцию α = α(Δx), стремящуюся к нулю при 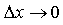 такую, что
такую, что
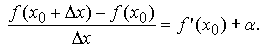
Но тогда 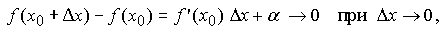 и, следовательно, функция f непрерывна при x = x0. Так как число x0 – произвольное, то функция fнепрерывна на всем интервале (a, b).
и, следовательно, функция f непрерывна при x = x0. Так как число x0 – произвольное, то функция fнепрерывна на всем интервале (a, b).
Теорема доказана.
Из доказанной теоремы непосредственно вытекает, что в точках разрыва функция не может быть дифференцируемой.
Однако из непрерывности функции на интервале (a, b) не следует дифферецируемость функции в каждой точке интервала (a, b). Например, функция 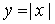 непрерывна на всей числовой прямой, но эта функция недифференцируема при x = 0. В самом деле, предел (1) не зависит от знака приращения аргумента Δx. Для функции же
непрерывна на всей числовой прямой, но эта функция недифференцируема при x = 0. В самом деле, предел (1) не зависит от знака приращения аргумента Δx. Для функции же 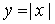 имеем, еслиx = 0придать приращение Δx > 0, то Δy = Δx, а еслиΔx < 0, то Δy = − Δx. Таким образом,
имеем, еслиx = 0придать приращение Δx > 0, то Δy = Δx, а еслиΔx < 0, то Δy = − Δx. Таким образом,
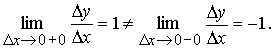
Следовательно, функция 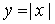 недифференцируема при x = 0.
недифференцируема при x = 0.
