Производная функции, её геометрический и физический смысл.

1⁰. Пусть функция 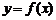определена и непрерывна в окрестности точки 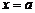. Если независимой переменной х придать приращение Dх в этой точке, то функция получит соответствующее приращение 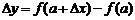. Если Dх®0, то, по определению непрерывной в точке 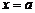функции, и Dу®0.

С целью исследования скорости изменения значений функции вводится понятие производной.

Производной функции 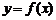в точке 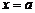называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю.

Для обозначения производной используются символы: 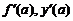. Таким образом, по определению

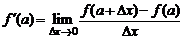. (1)

Операцию нахождения производной называют дифференцированием.

Если функция 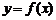имеет производную 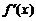в каждой точке 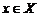, то производную 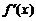можно рассматривать как функцию переменной х на множестве X.

Cуществуют односторонние пределы: 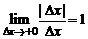и 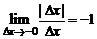, не равные между собой. Такимобразом, производная функции 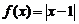в точке 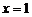не существует. □

Учитывая, что существуют вышеуказанные односторонние пределы, в этом случае говорят, что у рассматриваемой функции существуют односторонние производные в точке 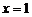(правая и левая соответственно).

Выясним связь между существованием производной и непрерывностью функции в заданной точке.

Функция может быть непрерывной в точке, но не иметь в ней производной

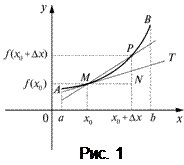
2⁰. Геометрический смысл производной. Пусть функция 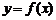определена на интервале 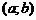. Предположим, что кривая АВ является графиком этой функции (рис. 1). Пусть 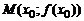– произвольная точка графика. Придадим аргументу 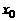приращение Dх. Соответствующую точку на графике обозначим через .

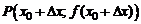Через точки М и Р проведем секущую. Найдем угловой коэффициент секущей, проходящей через точки М и Р. Ясно, что он вычисляется по формуле (см. рис. 1) 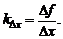Если точку Р устремить по кривой АВ к точке М, то положение секущей будет, вообще говоря, изменяться.

Если при 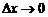существует предельное положение секущей, то полученная прямая называется касательной к графику 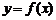в точке 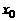. Понятно, что условием существования предельного положения секущей является существование следующего предела:

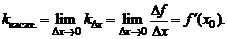
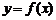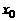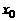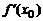Итак, график функции имеет касательную в точке тогда и только тогда, когда функция дифференцируема в точке и является угловым коэффициентом касательной.

Составим теперь уравнение касательной в точке 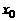как уравнение прямой, проходящей через точку 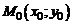, , 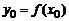имеющей угловой коэффициент, равный :

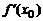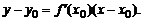(2)

Прямая, проходящая через точку 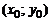и перпендикулярная касательной, называется нормалью к графику функции в этой точке. Учитывая условие перпендикулярности двух прямых, запишем уравнение нормали:

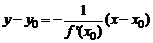(полагаем, что ).

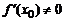Если 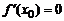, то нормалью будет прямая .

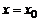3⁰. Физический смысл производной. Пусть некоторая материальная точка М движется прямолинейно и задан закон ее движения 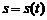,т.е. известно расстояние s(t) от точки М до некоторой начальной точки отсчета в каждый момент времени t. В момент времени 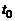точка пройдет расстояние 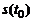, а в момент времени 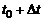– расстояние 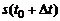. За промежуток времени 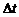точка М пройдет расстояние .

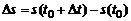Отношение 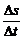можно рассматривать как среднюю скорость движения на промежутке времени 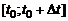.Чем меньше промежуток времени 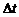, тем точнее соответствующая средняя скорость будет характеризовать движение точки в момент времени 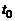. Поэтому предел средней скорости движения при 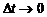называют скоростью движения (или мгновенной скоростью движения) точки М в момент времени 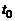и обозначают 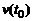, т.е.

.

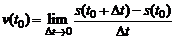Но выражение справа есть 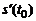. Таким образом, 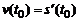, т.е. скорость движения в момент времени 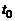есть производная от пройденного пути по времени.

Понятие скорости, заимствованное из механики, удобно использовать и при изучении произвольной функции. Какую бы зависимость не отражала функция 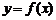, отношение 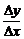есть средняя скорость изменения зависимой переменной y относительно аргумента x, а 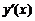есть скорость изменения y в точке x.

43.Правила дифференцирования, производная сложной и обратной функции. Производные элементарных функций.

43¹. Правила дифференцирования, производная сложной и обратной функции.

Если функци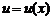и и 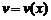имеют производныев точке x, то сумма, разность, произведение и частное этих функций также имеют производную в этой точке (частное при условии, что 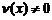) и справедливы следующие формулы:

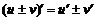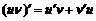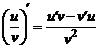, , . (1)

Производная обратной функции.

Утверждение 1. Если функция 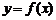строго монотонна и непрерывна в некоторой окрестности точки 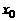, имеет производную в точке 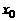и 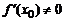, то обратная функция 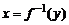имеет производную в соответствующей точке 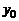, , 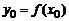причем .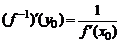