Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых функций. Эквивалентные функции и их применение к вычислению пределов.

36¹. Бесконечно малые и бесконечно большие функции.

Определение и основные свойства.Функция 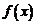называется бесконечно малой при 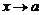, если .

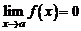Функция 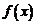называется бесконечно большой при 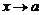, если .

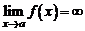Например, функция 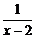есть бесконечно большая функция при .

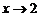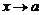
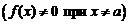Утверждение 1.Для того, чтобы функция при была бесконечно малой функцией, необходимо и достаточно, чтобы функция 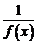была бесконечно большой функцией при .

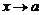Для бесконечно малой функции выполняются те же свойства, что и для бесконечно малых последовательностей.

Связь между функцией, ее пределом и бесконечно малой функцией.

Теорема 1. Для того, чтобы функция 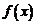имела предел в точке 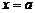, равный b, необходимо и достаточно, чтобы функция 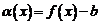была бесконечно малой функцией при .

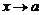36². Сравнение бесконечно малых функций.

Как известно, сумма, разность и произведение двух бесконечно малых функций есть функция бесконечно малая (см. § 6). Отношение же двух бесконечно малых функций может быть конечным числом или вообще не имеет предела.

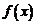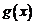Пусть и – бесконечно малые функции при 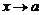, т.е. 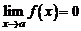и 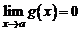. Тогда:

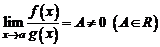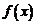1. Если , то и 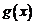называются бесконечно малыми одного порядка.

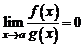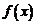2. Если , то называется бесконечно малой более высокого порядка, чем .

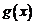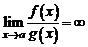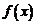3. Если , то называется бесконечно малой более низкого порядка, чем .

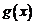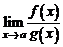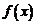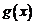4. Если не существует, то и называются несравнимыми бесконечно малыми функциями.

36³. Эквивалентные функции и их применение к вычислению пределов.

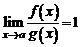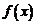Если , то и 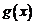называются эквивалентными бесконечно малыми функциями (при 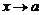) и обозначаются: 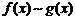при .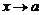

Например, 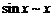при 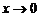, т. к. .

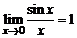Для эквивалентных бесконечно малых функций справедливы следующие утверждения:

1. Предел отношения двух бесконечно малых функций не изменится, если каждую (или одну из них) заменить эквивалентной ей бесконечно малой функцией.

2. Разность двух эквивалентных бесконечно малых функций есть бесконечно малая функция более высокого порядка, чем каждая из них.

3. Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.

Докажем последнее утверждение для двух функций.

Пусть 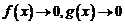при 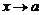, причем –
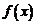бесконечно малая функция более высокого порядка, чем ,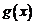
т.е. 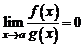. Тогда

.

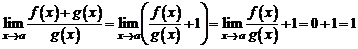Следовательно, 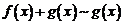при . □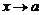

Слагаемое, эквивалентное сумме бесконечно малых функций, называется главной частью этой суммы.

Применение эквивалентных бесконечно малых функций к вычислению пределов.Для раскрытия неопределенностей вида 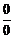часто бывает полезным применять замену бесконечно малой функции на эквивалентную ей.

Приведем важнейшие эквивалентности, которые используются при вычислении пределов:

1. 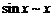при ;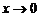

2.

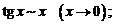
3.

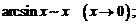
4.

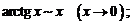
5.

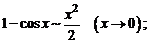
6.

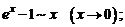
7.

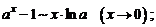
8.

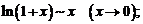
9.

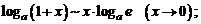
10. 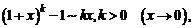в частности .

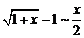Непрерывность функции в точке и на отрезке. Свойства функций, непрерывных в точке.

37¹. Непрерывность функции в точке и на отрезке.