Понятие функции. Предел функции в точке и на бесконечности. Односторонние пределы. Свойства функций, имеющих предел.

35¹. Понятие функции.

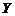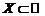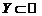Пусть Х и – два произвольных множества действительных чисел, т.е. и . Если каждому элементу х из множества Х по некоторому правилу f поставлен в соответствие вполне определенный элемент у из множества 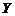, то говорят, что задана функция f. Для функции f используются следующие обозначения: .

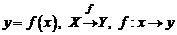Переменная х называется независимой переменной или аргументом функции, переменная у – зависимой переменной или функцией. Множество Х называют областью определения или областью существования функции f. Множество всех значений у, 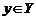,называется областью значений функции.

Значение 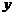, что соответствует определенному аргументу 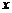при функциональной зависимости 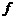, называют еще образом переменной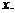

Функция 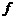каждому элементу области определения ставит в соответствие единственный элемент области значений.

Например, функция 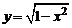определена на отрезке 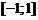, т.е. областью определения является множество 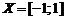. Множеством значений функции в данном случае является отрезок [0; 1], .

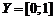Функция, все значения которой равны между собой, называется постоянной. Постоянную функцию часто обозначают буквой С.

Функция f, определенная на множестве X, называется ограниченной, если 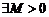такое, что 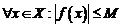. Например, функция 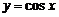является ограниченной на 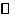, так как 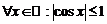, функция 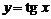не является ограниченной на интервале 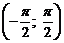, так как не существует числа 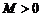такого, чтобы .

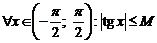Функция называется возрастающей (убывающей) на множестве Х, если для любых значений 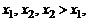из этого множества выполняется неравенство 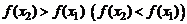. Если же для любых 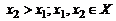выполняется 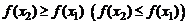, то функция называется неубывающей (невозрастающей) на множестве Х.

Функции всех указанных типов носят название монотонных. Такие функции часто встречаются в различных математических приложениях. Например, освещенность, меняющаяся по мере удаления от источника света, является монотонно убывающей функцией расстояния.

Графиком функции называется множество всех точек плоскости с координатами 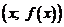, т.е. координаты х и 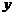точек графика связаны соотношением 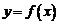. Например, графиком функции 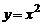является парабола. Естественно, что графиком функции не обязательно является «сплошная» кривая. В частности, графиком функции 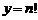будет бесконечное множество изолированных точек (постройте!).

Чтобы задать функцию, требуется указать правило: как по каждому значению аргумента х находить соответствующее значение функции 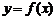. Существуют три основных способа задания функции: аналитический, табличный и графический.

35². функции в точке и на бесконечности.

1.Пусть функция f определена в некоторой окрестности точки 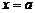за исключением, быть может, самой точки а. Возьмем последовательность точек 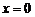из этой окрестности, сходящуюся в точке а. Значения функции в точках последовательности, в свою очередь, образуют последовательность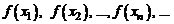

Число b называется пределом функции f в точке 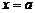(или при 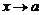), если для любой последовательности 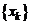, сходящейся к а, соответствующая последовательность значений функции 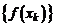сходится к b.

Для обозначения предела функции f в точке 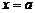используется запись .

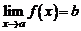2.Число b называется пределом функции при 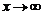, если для любой бесконечно большой последовательности 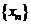соответствующая последовательность значений функции 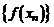сходится к b и обозначается .

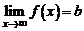Аналогично определяется предел функции при 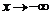: 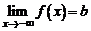и при

Рис. 3

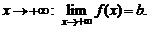
35³. Односторонние пределы.

В определении предела функции 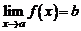считается, что х стремится к а любым способом: оставаясь меньше, чем а (слева от а) или больше, чем а (справа от а).

Бывают случаи, когда способ приближения аргумента х к а существенно влияет на значение предела функции. Поэтому вводят понятие односторонних пределов.

Число b называется правым пределом (пределом справа) в точке 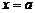, если для любой сходящейся к а последовательности 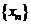, члены которой больше или равны а ( 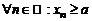), соответствующая последовательность 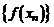сходится к b; обозначается: .

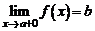Аналогично, число b называется левым пределом (слева) в точке 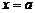, если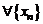 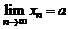, , 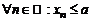соответствующая последовательность 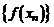сходится к b; обозначается: .

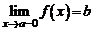Правый и левый пределы функций в точке называются односторонними. В случае, когда 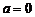, используются обозначения: , .

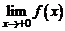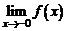Коротко предел слева и справа обозначают .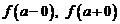

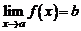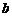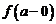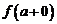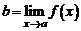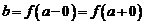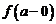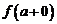Очевидно, если существует , то существуют и оба односторонних предела, причем совпадает с ними. Справедливо и обратное утверждение: если существуют оба предела , , и они равны, то существует предел и . Если же ¹ , то 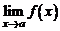не существует.

35⁴. Свойства функций, имеющих предел.

В приводимых ниже свойствах будем считать, что пределы 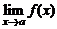и 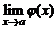существуют.

Свойство 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов: .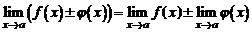

Следствие 1. Функция может иметь только один предел в точке .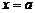

Свойство 2. Предел произведения двух функций равен произведению их пределов: .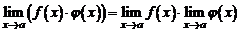

Следствие 2. а) Постоянный множитель можно выносить за знак предела:

.

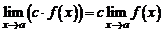б) Предел степени с натуральным показателем равен той же степени предела:

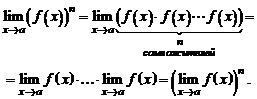
Свойство 3. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю:

.
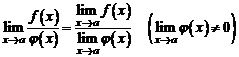