Понятие комплексного числа. Алгебраическая, тригонометрическая и показательная формы комплексного числа.
301. Понятие комплексного числа.
Комплексным числом z называется упорядоченная пара действительных чисел 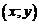 , которая записывается в виде
, которая записывается в виде 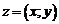 . Любое действительное число, согласно этому определению, можно записать
. Любое действительное число, согласно этому определению, можно записать 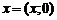 .
.
Два комплексных числа 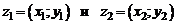 называются равными, если
называются равными, если 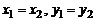 .
.
302. Алгебраическая, тригонометрическая и показательная формы комплексного числа.
1. Алгебраическая форма комплексного числа.
Среди комплексных чисел особое место занимает число 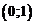 , которое называют мнимой единицей и обозначают через i:
, которое называют мнимой единицей и обозначают через i: 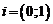 .
.
Согласно формуле (1.2) имеем 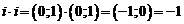 ,
,
т.е. 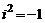 .
.
С помощью формул (1.1) и (1.2) получим:
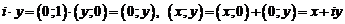 .
.
Т.е. каждое комплексное число 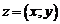 можно записать в виде
можно записать в виде
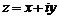 , (1)
, (1)
называемом алгебраической формой. При этом число x называют действительной частью комплексного числа z и обозначают 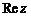 , а число y – мнимой частью и обозначают
, а число y – мнимой частью и обозначают 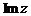 .
.
Если 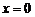 , то комплексное число
, то комплексное число 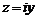 называют мнимым числом.
называют мнимым числом.
Сложение и умножение комплексных чисел в алгебраической форме выполняются по правилам действий с многочленами, заменяя 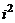 на
на 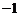 . Например, равенство (1.2) можно получить так:
. Например, равенство (1.2) можно получить так:
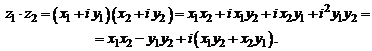
Множество комплексных чисел обозначают буквой 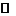 . Числа
. Числа 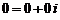 и
и 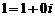 на множестве
на множестве  имеют те же самые свойства, что и на множестве
имеют те же самые свойства, что и на множестве  :
:
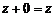 ,
, 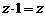 ,
, 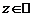 .
.
На множестве 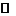 вычитание вводится как операция, обратная сложению. Для каждой пары комплексных чисел
вычитание вводится как операция, обратная сложению. Для каждой пары комплексных чисел 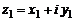 и
и 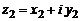 существует, и при том только одно, комплексное число z, такое, что
существует, и при том только одно, комплексное число z, такое, что
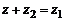 . (2)
. (2)
Действительно, из равенства (2), согласно правилу равенства и определению (1.1) суммы комплексных чисел, следует 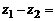
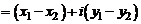 . В частности, разность
. В частности, разность 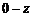 обозначают – z.
обозначают – z.
Деление на множестве 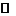 вводится как операция, обратная
вводится как операция, обратная
умножению, а частным от деления комплексного числа 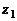 на число
на число 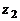 называют такое число z, что имеет место равенство
называют такое число z, что имеет место равенство
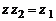 , (3)
, (3)
и обозначают 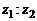 или
или 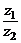 .
.
2. тригонометрическая и показательная формы комплексного числа.
Пусть 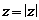 есть модуль комплексного числа z, а
есть модуль комплексного числа z, а 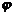 – угол между положительным направлением действительной оси и вектором z, который отсчитывается от положительного направления действительной оси (рис.3. 1). Этот угол называют аргументом комплексного числа
– угол между положительным направлением действительной оси и вектором z, который отсчитывается от положительного направления действительной оси (рис.3. 1). Этот угол называют аргументом комплексного числа 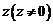 и обозначают
и обозначают 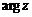 .
.
Для числа 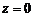 аргумент не определяется, поэтому далее, при использовании
аргумент не определяется, поэтому далее, при использовании 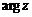 , будем считать, что
, будем считать, что 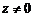 .
.
Очевидно (рис. 3.1), что
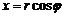 ,
, 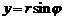 . (1)
. (1)
Отсюда следует, что всякое комплексное число 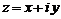 представляется в виде
представляется в виде
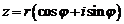 . (2)
. (2)
Запись комплексного числа 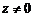 в виде (2) называют тригонометрической формой комплексного числа.
в виде (2) называют тригонометрической формой комплексного числа.
Из формул (3.1) и (1), учитывая, что 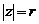 , находим:
, находим:
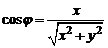 ,
, 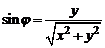 . (3)
. (3)
Система (3) имеет бесконечно много решений вида 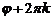 ,
,
где 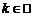 .
.
*****
Пусть имеем
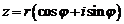 . (7)
. (7)
Определим показательную функцию 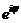 с помощью формулы Эйлера
с помощью формулы Эйлера
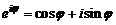 . (8)
. (8)
Тогда (7) примет вид
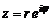 . (9)
. (9)
Форма (9) называется показательной формой комплексного числа.
С помощью формулы (9) легко получаем правила умножения и деления комплексных чисел в показательной форме
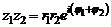 ,
, 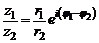 .
.
Это множество обозначается 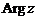 , при этом
, при этом 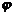 – значение аргумента комплексного числа, которое принадлежит полуинтервалу
– значение аргумента комплексного числа, которое принадлежит полуинтервалу 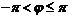 , называется главным значением и обозначается
, называется главным значением и обозначается 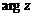 .
.
Используя (3), получим 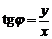 . Тогда
. Тогда 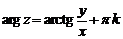 , где
, где 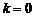 при
при 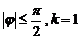 при
при 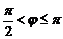 и
и 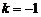 при
при 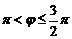 .
.
