Различные виды уравнений прямой на плоскости. Взаимное расположение двух прямых на плоскости. Угол между прямыми. Расстояние от точки до прямой.
121. Различные виды уравнений прямой на плоскости.
А)Уравнение прямой с угловым коэффициентом. Рассмотрим прямую, не перпендикулярную оси 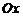 . Назовем углом наклона данной прямой к оси
. Назовем углом наклона данной прямой к оси 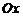 угол
угол 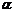 , на который нужно повернуть ось
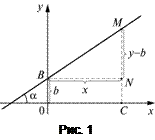
, на который нужно повернуть ось 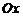 против часовой стрелки, чтобы ее положительное направление совпало с одним из направлений прямой (рис.1). Тангенс угла наклона прямой к оси
против часовой стрелки, чтобы ее положительное направление совпало с одним из направлений прямой (рис.1). Тангенс угла наклона прямой к оси 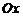 называют угловым коэффициентом и обозначают буквой
называют угловым коэффициентом и обозначают буквой 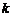 :
:
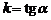 . (1)
. (1)
 Если
Если 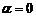 , т.е. прямая параллельна оси
, т.е. прямая параллельна оси 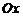 , то
, то 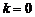 . Если
. Если 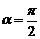 , то есть прямая перпендикулярна оси
, то есть прямая перпендикулярна оси 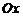 , то выражение
, то выражение 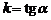 не имеет смысла. Тогда говорят, что угловой коэффициент «обращается в бесконечность».
не имеет смысла. Тогда говорят, что угловой коэффициент «обращается в бесконечность».
Если известен угловой коэффициент прямой и величина отрезка 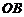 , который прямая отсекает на оси
, который прямая отсекает на оси 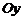 , то прямая определяется уравнением
, то прямая определяется уравнением
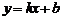 .. (2)
.. (2)
Уравнение (2) называют уравнением прямой с угловым коэффициентом 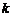 . Если
. Если 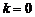 , то прямая параллельна оси
, то прямая параллельна оси 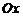 , и ее уравнение имеет вид
, и ее уравнение имеет вид 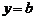 .
.
Итак, любая прямая, не перпендикулярная оси 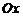 , имеет уравнение вида (2). Верно и обратное: любое уравнение вида (2) определяет прямую, которая имеет угловой коэффициент
, имеет уравнение вида (2). Верно и обратное: любое уравнение вида (2) определяет прямую, которая имеет угловой коэффициент 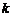 и отсекает на оси
и отсекает на оси 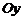 отрезок, величина которого равна
отрезок, величина которого равна 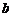 .
.
Б)Уравнение прямой, проходящей через данную точку, с данным угловым коэффициентом. Если известно, что угловой коэффициент прямой равен 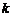 , и прямая проходит через точку
, и прямая проходит через точку 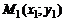 , то уравнение такой прямой имеет вид
, то уравнение такой прямой имеет вид
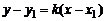 .
.
В)Уравнение прямой, проходящей через две данные точки. Прямая, проходящая через заданные точки 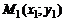 и
и 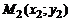 определяется уравнением
определяется уравнением
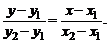
Если 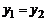 , то уравнение искомой прямой имеет вид
, то уравнение искомой прямой имеет вид 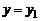 и такая прямая параллельна оси
и такая прямая параллельна оси 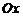 . Если
. Если 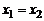 , то прямая, проходящая через точки
, то прямая, проходящая через точки 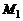 и
и 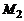 , параллельна оси
, параллельна оси 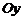 , ее уравнение имеет вид
, ее уравнение имеет вид 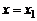 .
.
С)Общее уравнение прямой.
Утверждение 1.В прямоугольной системе координат любая прямая задается уравнением первой степени
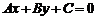 , (2)
, (2)
и, обратно, уравнение (2) при произвольных коэффициентах 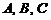 (
( 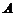 и
и 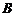 одновременно не равны нулю) определяет прямую в прямоугольной системе координат
одновременно не равны нулю) определяет прямую в прямоугольной системе координат 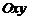 .
.
Линии, определяемые уравнениями вида (2) называются линиями первого порядка. Уравнение 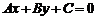 называется общим уравнением прямой. При различных значениях
называется общим уравнением прямой. При различных значениях 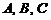 оно определяет все возможные прямые.
оно определяет все возможные прямые.
Д)Неполные уравнения первой степени. Уравнение прямой в «отрезках».Рассмотрим три частных случая, когда уравнение 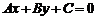 является неполным, т.е. один из коэффициентов равен нулю:
является неполным, т.е. один из коэффициентов равен нулю:
1) 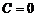 ; уравнение имеет вид
; уравнение имеет вид 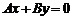 и определяет прямую, проходящую через начало координат;
и определяет прямую, проходящую через начало координат;
2) 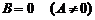 ; уравнение имеет вид
; уравнение имеет вид 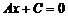 и определяет прямую, параллельную оси
и определяет прямую, параллельную оси 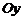 . В частности, уравнение
. В частности, уравнение 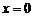 определяет ось ординат;
определяет ось ординат;
3) 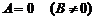 ; уравнение имеет вид
; уравнение имеет вид 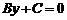 и определяет прямую, параллельную оси
и определяет прямую, параллельную оси 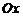 . В частности, уравнение
. В частности, уравнение 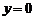 определяет ось абсцисс.
определяет ось абсцисс.
Если ни один из коэффициентов 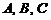 не равен нулю, то уравнение (2) приводится к виду
не равен нулю, то уравнение (2) приводится к виду
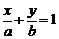 ,
,
который называется уравнением прямой «в отрезках». Числа 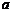 и
и 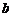 является величинами отрезков, которые прямая отсекает на осях координат. Эта форма уравнения удобна для геометрического построения прямой.
является величинами отрезков, которые прямая отсекает на осях координат. Эта форма уравнения удобна для геометрического построения прямой.
122. Взаимное расположение двух прямых на плоскости.
Пусть прямые 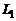 и
и 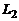 заданы уравнениями:
заданы уравнениями:
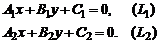 (2)
(2)
Если 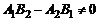 , то прямые L1 и L2 пересекаются в одной точке с координатами
, то прямые L1 и L2 пересекаются в одной точке с координатами
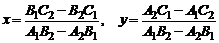 .
.
Пусть теперь 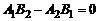 . Возможны два случая:
. Возможны два случая:
1. 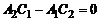 и
и 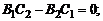 Тогда имеем
Тогда имеем 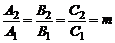 , где
, где 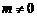 – некоторое число, и уравнения (2) определяют одну и ту же прямую.
– некоторое число, и уравнения (2) определяют одну и ту же прямую.
2. 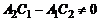 (
( 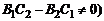 . В этом случае прямые L1 и L2 параллельны
. В этом случае прямые L1 и L2 параллельны
Итак, две прямые на плоскости либо пересекаются в одной точке, либо совпадают, либо параллельны.
123. Угол между прямыми.
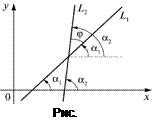 Рассмотрим две прямые
Рассмотрим две прямые 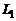 и
и 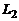 . Пусть уравнение
. Пусть уравнение 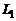 имеет вид
имеет вид 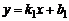 , где
, где 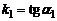 , уравнение
, уравнение 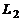 – вид
– вид 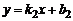 , где
, где 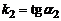 , а
, а 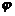 – угол между прямыми
– угол между прямыми 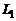 и
и 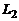 ,
, 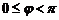 (рис.1).
(рис.1).
Тогда один из углов между прямыми определяется условием
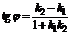 , (1)
, (1)
а второй угол равен 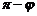 .
.
124. Расстояние от точки до прямой.
Расстояние от точки 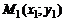 до прямой, заданной общим уравнением
до прямой, заданной общим уравнением 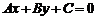 , определяется равенством
, определяется равенством
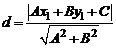 .
.
Эллипс. Его характеристики.
 Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек
Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек 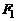 и
и 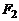 , называемых фокусами, есть величина постоянная, равная
, называемых фокусами, есть величина постоянная, равная 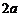 .
.
Выберем декартову систему координат 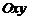 так, чтобы ось
так, чтобы ось 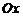 проходила через фокусы
проходила через фокусы 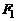 и
и 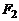 , расстояние между которыми обозначим
, расстояние между которыми обозначим 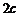 , а начало координат О находилось в середине отрезка
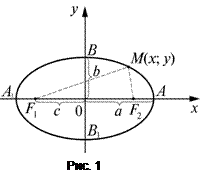
, а начало координат О находилось в середине отрезка 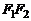 (рис. 1). В такой системе координат уравнение эллипса будетиметь вид
(рис. 1). В такой системе координат уравнение эллипса будетиметь вид
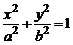 . (1)
. (1)
Уравнение (1) называется каноническим уравнением эллипса. Параметр 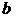 определяется равенством
определяется равенством 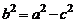 . Эллипс симметричен относительно обеих осей координат. Эллипс пересекает ось
. Эллипс симметричен относительно обеих осей координат. Эллипс пересекает ось 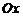 в двух точках:
в двух точках: 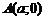 и
и 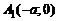 ; пересекает ось
; пересекает ось 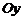 в двух точках:
в двух точках: 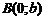 и
и 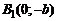 . Эти четыре точки называют вершинами эллипса. Отрезок
. Эти четыре точки называют вершинами эллипса. Отрезок 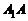 называется большой осью эллипса, а отрезок
называется большой осью эллипса, а отрезок 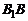 – его малой осью. Здесь
– его малой осью. Здесь 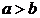 .
.
Уравнение (1) можно рассматривать и в случае 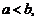 тогда оно определяет эллипс с большой полуосью
тогда оно определяет эллипс с большой полуосью 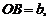 фокусы такого эллипса лежат на оси Oy.
фокусы такого эллипса лежат на оси Oy.
В случае, когда 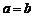 , уравнение (1) имеет вид
, уравнение (1) имеет вид 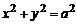 и определяет окружность радиуса а с центром в начале координат. В этом случае
и определяет окружность радиуса а с центром в начале координат. В этом случае 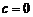 .
.
Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси, т.е.
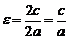 .
.
Поскольку 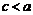 , то для любого эллипса
, то для любого эллипса 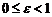 , причем случай
, причем случай 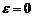 соответствует окружности.
соответствует окружности.
Геометрически 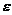 характеризует степень сжатия эллипса: чем больше
характеризует степень сжатия эллипса: чем больше 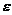 , тем больше вытянут эллипс.
, тем больше вытянут эллипс.
Две прямые, перпендикулярные большой оси эллипса и расположенные симметрично относительно центра на расстоянии 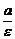 от него, называются директрисами эллипса.
от него, называются директрисами эллипса.
Если эллипс задан каноническим уравнением (1), то уравнения директрис имеют вид
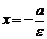 и
и 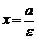 .
.
Так как 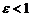 , то
, то 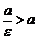 . Откуда заключаем, что правая директриса расположена правее правой вершины эллипса, а левая – левее его левой вершины.
. Откуда заключаем, что правая директриса расположена правее правой вершины эллипса, а левая – левее его левой вершины.
