Если нет ответа – частичная УАО

Понятие БАО. Примеры

Говорят, что на множестве М (М не равно 0) задано БАО, если любым 2м а,в принадлежащим М по некоторому закону сопоставляется вполне определенный элемент а*в из этого же множества.

Примеры:

1)Сложение и умножение

2)Деление — частичная БАО на числовых множествах N, N₀,Z, Q,R, т.к. результата иногда нет (деление на 0)

3) на множестве всех точек плоскости а*а=а

4) на N

29*1951=21

1994*1994=14

(Если N₀, то не БАО 0*12=02)

Свойства БАО. Примеры

1. БАО называется коммутативной, если всегда а*в=в*а

Примеры:

• сложение и умножение чисел
• множество всех точек плоскости
• некоммутативное БАО –29*1951=21 (1*2 не всегда равно 2*1)

2. БАО называется ассоциативной если всегда (а*в)*с= а*(в*с)

Примеры:

• сложение и умножение чисел
• 29*1951=21((а*в)-двузначное число, первая цифра которого является первой цифрой а. Следовательно,лев.часть – двузначное число, у которого первая цифра числа а – это первая цифра числа а, а последняя – последняя цифра числа с. Аналогично устроена правая часть).
• неассоциативная: множество всех точек плоскости

У каждого числа есть 1 и последняя цифра. (a*b) – двузначное число, у которого 1 цифра – это цифра числа a => левая часть – двузначное число, у которого 1 цифра – это 1 цифра числа a, а 2 – последняя цифра числа c. Аналогично устроена правая часть.

a*b*c*d = a₁d_n

л.ч. не равнап.ч. => ассоциативности нет.

3. БАО называется идемпотентной, если всегда а*а=а

Примеры:

• на множестве всех точек плоскости а*а=а
• аՈUa=a
• 27*789=29 – не идемпотентно, т.к.1*2 не всегда=2*1

4. Элемент е из М называется правым нейтральным элементом БАО (на М), если всегда а*е=а

Аналогично — левый: е*а=а

Если он и левый, и правый, то его называют нейтральным.

Примеры:

• 0-е сложения, а 1-е умножения.
• На N: 1-е правый нейтральный элемент деления
• 0-е правый нейтральный элемент вычитания.

5. uϵM называется правым поглощающим элементом БАО* (на М), если всегда а*u=u

аналогично — левый: u*а=u

Если он и левый, и правый, то его называют поглощающим.

Примеры:

• 0-uпоглощающий элемент умножения
• 0-uлевый поглощающий элемент деления

6. БАО* называется право-(лево-) дистрибутивной относительно БАО, если всегда (а^ов)*с=(а*с)^о(в*с)

Аналогично – леваядистрибутивность:

(а*с)^о(в*с)=(а^ов)*с

Если он и лево- и праводистр., то его называют дистрибутивным.

Примеры:

• Умножение дистрибутивно относительно сложения и вычитания.

(а+в)∙с=а∙с+в∙с

· Умнож и дел.

· Возведение в степень

• В школе сложение недистрибутивно(распределительный закон) относительно умножения:(а∙в)+с= не всегда (а+с) ∙(в+с)
• Деление праводистр. относительно сложения и вычитания.

3. Понятие и примеры унарных алгебраических операций(УАО)

Говорят, что на множестве М (М не равно 0) задано УАО, если любой элемент а, принадлежащий М, по некоторому закону сопоставляется вполне определенный элемент а*а из этого же множества.

Примеры:

1) на Z нахождение противоположного числа (для 2 – -2, 0 – 0)

2) на R₊ нахождение обратного числа (для 2 – 1/2, 1/3 – 3)

а на R_–– это частичное УАО (для 0 нет обратного числа)

Если 1 ответ – УАО

Частичные БАО и УАО. Примеры

Если 1 ответ – УАО

Логические парадоксы.

Парадокс – досл. «рядом с верой».

Парадокс «Протагор и Эватл»

Эватл обучался праву у Протагора. По заключенному между ними договору, он должен был заплатить Протагору за обучение лишь в том случае, если выиграет свой первый судебный процесс. И наоборот, если он проиграет этот процесс, то не должен будет платить ничего. Закончив обучение, Эватл не стал участвовать в судебных процессах. Устав ждать, Протагор подал в суд на своего ученика. Свое требование он обосновал так:

- Каким бы не было решение суда, Эватл должен будет заплатить мне. Он либо выиграет этот свой первый процесс, либо проиграет. Если выиграет, то заплатит в силу нашего договора. Если проиграет, то заплатит согласно решению суда.

На что Эватл ответил:

- Действительно, я либо выиграю этот процесс, либо проиграю его. Если выиграю, суд освободит меня от обязанности платить. Если же решение суда будет не в мою пользу, то значит я проиграл свой первый процесс и не заплачу в силу нашего договора.

ОСНОВА ТЕОРИИ МНОЖЕСТВ

Понятие множества. Примеры. Равные множества. Основные числовые множества. Конечные и бесконечные множества.

Множество – это простейшее мат понятие, кот нельзя дать формального определения, подобно понятию точки, не сводится к другим понятиям математики и не определяется.

Понятие мн-ва может быть пояснено при помощи примеров: можно говорить о мн-ве всех учеников одной школы, о мн-ве всех людей на Земле, о мн-ве всех картофелин на картофельном поле, мн-ве целых чисел.

Предметы (объекты любой природы), составляющие некоторое мн-во, наз его элементами.

Объект хяв-ся элементом мн-ваА, записывают так: х∈А (читается: х принадлежит А). Если объект х не яв-ся элементомА, то это записывают так: х∉ А (читается: xне принадлежит А).

Например: еслиА есть мн-во всех четных натуральных чисел, то 2 ∈А, 1024 ∈А, 7 ∉А, ¾ ∉ А.

Мн-во, не имеющее ни одного элемента, называетсяпустым множеством. Пустое множество обозначается так: Ø.

Мн-во считают заданным, если о любом объекте можно сказать, принадлежит он этому мн-вуили нет.

Равные множества

Равными множествами называются мн-ва, состоящие из одних и тех же элементов.

Например: если А={1,2,3,4}, B={3,1,4,2} то А=В. Можно утверждать, что 2 мн-ва равны, если каждое из них явл. подмножеством другого. А=В ⇔ (знак равносильно, тогда и только тогда) (А ⊂ В и В⊂ А).

Множества не равны, если хотя бы в одном мн-ве существует хотя бы 1 элемент, не принадлежащий другому мн-ву.

Например:мн-во всех девушек нашей группы и всех студентов нашей группы.

Основные числовые множества

Если элементами мн-ваявл. числа, то их называют числовыми множествами.

Примеры:мн-во всех целых чисел, мн-во всех рациональных чисел, мн-во всех действительных чисел. Каждое непустое мн-во А имеет два подмн-ва: пустое мн-во и само мн-во А.

Перечислением его элементов

Например: мн. A = {b,c,d} задано точным перечислением всех его элементов (так можно задать лишь конечное множество)

Понятие подмножества

Множество называется конечным, если все его элементы можно перечислить.

Например: множество натуральных чисел – бесконечное. Для того, чтобы удобно было представить множество, их принято обозначать кругами Эйлера (см. рисунок).

Мн. A называют частью или подмножеством другого множества B, если каждый элемент из мн. Aявл. элементом множества B.

Например: множество всех прямоугольников включается в множество параллелограммов.

Каждое пустое мн. Aимеет по крайней мере 2 подмножества: пустое мн. и само мн. A. Пустое множества считается подмножеством любого множества.

Множества могут находиться в различных отношениях:

1) множества не имеют общих элементов

A = {a,b,c} B = {m,n}

2) множества имеют некоторые общие элементы

A = {a,b,c,d} B = {m,n,a,d}

3) A подмножество множества B (все элементы мн. A принадлежат мн. B)

A = {a,b,c} B = {a,m,n,b,c,f}

4) все элементы A принадлежат B и все эл. B принадлежат A.

A = {a,b,c} B = {c,a,b}

Основа теории множеств:
8. Понятие множества. Примеры. Равные множества. Основные числовые множества. Конечные и бесконечные множества. Диаграммы Эйлера и их применение. Способы задания множеств.Основа теории множеств:
8. Понятие множества. Примеры. Равные множества. Основные числовые множества. Конечные и бесконечные множества. Диаграммы Эйлера и их применение. Способы задания множеств.Основа теории множеств:
8. Понятие множества. Примеры. Равные множества. Основные числовые множества. Конечные и бесконечные множества. Диаграммы Эйлера и их применение. Способы задания множеств.Основа теории множеств:
8. Понятие множества. Примеры. Равные множества. Основные числовые множества. Конечные и бесконечные множества. Диаграммы Эйлера и их применение. Способы задания множеств.10. Основные операции над множествами: объединение, пересечение, вычитание, дополнение до универсального (УАО), симметрическое вычитание, декартого умножение. Свойства.

Вычитание множеств.

Определение:

Разностью множеств A и B называется множество A – B, состоящее из тех и только тех элементов множества A, которые не являются элементами множества B.

Например:

Для А = {1,2,3,4,5} и B = {2,4,6}

А – В = {1,3,5}

Например:

Если А – множество всех ромбов, а В – прямоугольников, то А – В = множество всех ромбов, кроме квадратов, а В – А = множество, состоящее из всех прямоугольников, которые не являются квадратами.

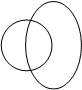А В

А – В (левое ухо)

Теорема о свойствах:

Вычитание – операция для нахождения разности (БАО).

Всегда:

1^о. А – Ø = А (Ø – правый нейтральный элемент)

2^о. Ø – А = Ø (Ø – левый поглощающий элемент) (см. определение и рисунок)

3^о. А – А = Ø

4^о. А – В = А – (А пересечение В)

Доказательство:

см. определение и рисунок.

Понятие БАО. Примеры

Говорят, что на множестве М (М не равно 0) задано БАО, если любым 2м а,в принадлежащим М по некоторому закону сопоставляется вполне определенный элемент а*в из этого же множества.

Примеры:

1)Сложение и умножение

2)Деление — частичная БАО на числовых множествах N, N₀,Z, Q,R, т.к. результата иногда нет (деление на 0)

3) на множестве всех точек плоскости а*а=а

4) на N

29*1951=21

1994*1994=14

(Если N₀, то не БАО 0*12=02)

Свойства БАО. Примеры

1. БАО называется коммутативной, если всегда а*в=в*а

Примеры:

• сложение и умножение чисел
• множество всех точек плоскости
• некоммутативное БАО –29*1951=21 (1*2 не всегда равно 2*1)

2. БАО называется ассоциативной если всегда (а*в)*с= а*(в*с)

Примеры:

• сложение и умножение чисел
• 29*1951=21((а*в)-двузначное число, первая цифра которого является первой цифрой а. Следовательно,лев.часть – двузначное число, у которого первая цифра числа а – это первая цифра числа а, а последняя – последняя цифра числа с. Аналогично устроена правая часть).
• неассоциативная: множество всех точек плоскости

У каждого числа есть 1 и последняя цифра. (a*b) – двузначное число, у которого 1 цифра – это цифра числа a => левая часть – двузначное число, у которого 1 цифра – это 1 цифра числа a, а 2 – последняя цифра числа c. Аналогично устроена правая часть.

a*b*c*d = a₁d_n

л.ч. не равнап.ч. => ассоциативности нет.

3. БАО называется идемпотентной, если всегда а*а=а

Примеры:

• на множестве всех точек плоскости а*а=а
• аՈUa=a
• 27*789=29 – не идемпотентно, т.к.1*2 не всегда=2*1

4. Элемент е из М называется правым нейтральным элементом БАО (на М), если всегда а*е=а

Аналогично — левый: е*а=а

Если он и левый, и правый, то его называют нейтральным.

Примеры:

• 0-е сложения, а 1-е умножения.
• На N: 1-е правый нейтральный элемент деления
• 0-е правый нейтральный элемент вычитания.

5. uϵM называется правым поглощающим элементом БАО* (на М), если всегда а*u=u

аналогично — левый: u*а=u

Если он и левый, и правый, то его называют поглощающим.

Примеры:

• 0-uпоглощающий элемент умножения
• 0-uлевый поглощающий элемент деления

6. БАО* называется право-(лево-) дистрибутивной относительно БАО, если всегда (а^ов)*с=(а*с)^о(в*с)

Аналогично – леваядистрибутивность:

(а*с)^о(в*с)=(а^ов)*с

Если он и лево- и праводистр., то его называют дистрибутивным.

Примеры:

• Умножение дистрибутивно относительно сложения и вычитания.

(а+в)∙с=а∙с+в∙с

· Умнож и дел.

· Возведение в степень

• В школе сложение недистрибутивно(распределительный закон) относительно умножения:(а∙в)+с= не всегда (а+с) ∙(в+с)
• Деление праводистр. относительно сложения и вычитания.

3. Понятие и примеры унарных алгебраических операций(УАО)

Говорят, что на множестве М (М не равно 0) задано УАО, если любой элемент а, принадлежащий М, по некоторому закону сопоставляется вполне определенный элемент а*а из этого же множества.

Примеры:

1) на Z нахождение противоположного числа (для 2 – -2, 0 – 0)

2) на R₊ нахождение обратного числа (для 2 – 1/2, 1/3 – 3)

а на R_–– это частичное УАО (для 0 нет обратного числа)

Если 1 ответ – УАО

Если нет ответа – частичная УАО

3) УАО нахождение след.числаN, N0, Z

Частичные БАО и УАО. Примеры