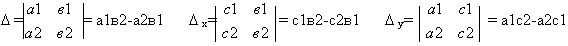Пирамида. Усеченная пирамида(есть в 3 билете)

Билет№10(16)

1)Определеный интеграл и его значение:Определенным интегралом от a до b непрерывной функции y=f(x), определенной на интервале [a;b] , называется приращение первообразной F(x) для этой функции, то есть

Числа a и b называются нижним и верхним пределами интегрирования.
Площать S криволинейной трапеции (фируры, ограниченной графиком непрерывной положительной на интервале [a;b] функции y=f(x), осью OX и прямыми x = a и x = b вычисляется по формуле:

2)Шар и Сфера:

Сфе́ра — это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы). Расстояние от точек сферы до её центра называется радиусом сферы и обычно обозначается R. Радиусом также называется любой отрезок, соединяющий точку сферы с её центром. Сфера – это граница шара. Центр, радиус и диаметр сферы являются также центром, радиусом и диаметром шара. Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии не более чем на данное расстояние. Другими словами, шар – это объединение сферы и всех ее внутренних точек.

Шар Сфера

Билет№11

1)Системы уравнений и неравенств . Способы решения систем уравнений( подстановкой ,сложения, графический , с Крамера)Метод подстановки. 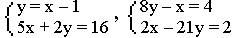1.Выразить у через х из одного уравнения системы.

2.Подставить полученное выражение вместо у в другое уравнение системы.3.Решить полученное уравнение относительно х.4.Подставить поочередно каждый из найденных на 3 шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.5.Записать ответ в виде пар значений (х;у).Метод КрамераОдним из основных методов решения данной системы является метод Крамера или метод определителей. По коэффициентам данной системы составляем три определителя: (главный), _х – определитель неизвестного х; _у – определитель неизвестного у.

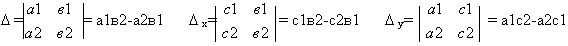
Пирамида. Усеченная пирамида ( билет № 3 там есть)

Билет №12(15)

Схема исследования функции

1. Найти область определения функции;
2. Исследовать функцию на четность, нечетность, периодичность;

3. Найти точки пересечения графика функции с осями координат;

4. Исследовать функцию на монотонность, то есть найти промежутки возрастания и убывания функции;

5. Найти точки экстремума и экстремальные значения функции;

Построить график функции.

Билет

1)Производная. Ее геометрический и физический смысл.

Физический (механический) смысл производной состоит в следующем. Если s(t) — закон прямолинейного движения тела, то производная выражает мгновенную скорость в момент времени t: v=s′(t).

Мгновенная скорость прямолинейного движения.

Ускорение прямолинейного движения.

Величина тока.

Геометрический смысл производной состоит в следующем. Если к графику функции y=f(x) в точке с абсциссой x=a можно провести касательную, непараллельную оси y, то f′(a) выражает угловой коэффициент касательной:

k=f′(a).

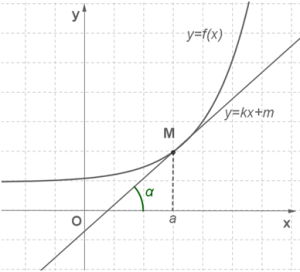
Поскольку k=tgα, то верно равенство f′(a)=tgα.

2) Вероятность

Теория вероятностей — это область математики, которая изучает случайные события и общие свойства событий, процессов.

В теории вероятностей эксперименты называются опытами, а возможные результаты — исходами. Все возможные исходы вместе создают множество исходов.

Любое утверждение о результате опыта, правильность которого возможно проверить, называется событием.

Событие, которое не может произойти, называется невозможным событием.

Событие, которое происходит всегда, называется достоверным событием.

Усло́вная вероя́тность — вероятность одного события при условии, что другое событие уже произошло.

Теорема. Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий

Теорема сложения вероятностей позволяет вычислять вероятности суммы двух или нескольких событий. Для двух событий теорема формулируется следующим образом.

Вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения: P(A+B)= P(A) + P(B) – P(AB).

Билет№14

1)Системы уравнений и неравенств . Способы решения систем уравнений( подстановкой ,сложения, графический , с Крамера)Метод подстановки. 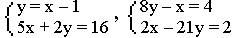1.Выразить у через х из одного уравнения системы.

2.Подставить полученное выражение вместо у в другое уравнение системы.3.Решить полученное уравнение относительно х.4.Подставить поочередно каждый из найденных на 3 шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.5.Записать ответ в виде пар значений (х;у).Метод КрамераОдним из основных методов решения данной системы является метод Крамера или метод определителей. По коэффициентам данной системы составляем три определителя: (главный), _х – определитель неизвестного х; _у – определитель неизвестного у.

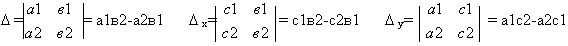
❷Признаки перпендикулярности прямой и плоскости: 1) Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости. 2) Если плоскость перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой. Наклонная к плоскости.Прямая, пересекающая плоскость и не перпендикулярная ей, называется наклонной к плоскости. Теорема о трех перпендикулярах. Наклонная к плоскости перпендикулярна к прямой, лежащей в этой плоскости, тогда и только тогда, когда проекция наклонной перпендикулярна этой прямой. Теорема, обратная теореме о трех перпендикулярах. Прямая, проведённая в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции.

Признак перпендикулярности плоскостей:если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. Теорема об общем перпендикуляре к двум скрещивающимся прямым.Для любых двух скрещивающихся прямых существует единственный общий перпендикуляр.

Билет№19

1)Системы уравнений и неравенств . Способы решения систем уравнений( подстановкой ,сложения, графический , с Крамера)Метод подстановки. 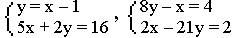1.Выразить у через х из одного уравнения системы.

2.Подставить полученное выражение вместо у в другое уравнение системы.3.Решить полученное уравнение относительно х.4.Подставить поочередно каждый из найденных на 3 шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.5.Записать ответ в виде пар значений (х;у).Метод КрамераОдним из основных методов решения данной системы является метод Крамера или метод определителей. По коэффициентам данной системы составляем три определителя: (главный), _х – определитель неизвестного х; _у – определитель неизвестного у.