Аксиомы стереометрии . Параллельность прямой и плоскости.
Аксиомы стереометрии состоят из 9 аксиом планиметрии и 3 аксиом группы С
Аксиомы группы С
1. Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.
2. Если две разные плоскости имеют общую точку, то они имеют и общую прямую, проходящую через эту точку.
3. Если две разные прямые имеют общую точку, то через них можно провести плоскость, и притом единственную.
4. Для произвольной плоскости выполняются аксиомы планиметрии.
Аксиомы стереометрии.
1. Какова не была прямая сущ. 2 точки, принадлежащие ей и не принадлежащие. Через любые 2 точки можно провести прямую, и только одну.
2. Прямая разбивает плоскость на 2 полуплоскости.
3. На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины и только один.
4. Из 3 точек на прямой и только 1 лежит между двумя.
Параллельность прямой и плоскости
ОпределениеПрямая и плоскость называются параллельными, если они не имеют общих точек. Если прямая a параллельна плоскости α, то пишут a || α.
Теорема 2.4. Признак параллельности прямой и плоскости .Если прямая вне плоскости параллельна какой-нибудь прямой на плоскости, то эта прямая параллельна и самой плоскости.
Теорема 2.5. Теорема о следе.
Если плоскость β проходит через прямую a, параллельную плоскости α, и пересекает эту плоскость по прямой b, то b || a.
Билет№3 ( №18)
1) Логарифмы . десятичные и натуральные лагорифмы
Логарифм, взятый по основанию 10, носит название — десятичный логарифм.
Десятичные логарифмы принято обозначать так: lg. Десятичный логарифм единицы равен нулю.
Десятичный логарифм чисел 10, 100, 1000 равен соответвенно 1, 2, 3, и т.д. т.е., имеют столько положительных единиц, сколько нулей стоит после единицы.
Десятичный логарифм чисел 0.1, 0.01, 0.001 равен соответвенно -1,-2, -3, и т.д. т.е. имеют столько отрицательных единиц сколько нулей стоит перед единицей, считая и ноль целых.
Десятичный логарифм других чисел имеет дробную часть. log10(N)=lgN.
Натуральный логарифм — это логарифм по основанию e, где e -иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), loge(x) или иногда просто log(x), если основание e подразумевается.
2)Пирамида . Усеченная пирамида.
Пирамида- тело поверхность которого состоит из основания, точки основания не лежащей на основ. И всех отрезков соединяющих вершину пирамиды с точками основания.
Высота пирамиды -перпендикуляр опущенный из вершины пирамиды к основанию.
Апофемой -высота боковой грани.
Усеченная пирамида-тело заключенное между 2-мя основаниями.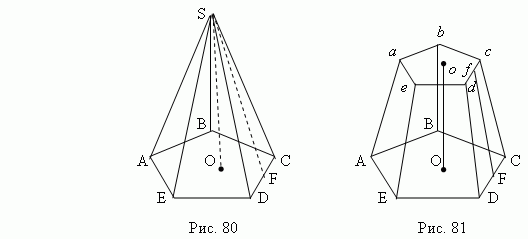 
Билет№4
❶Определение. Функция F (x) называется первообразной для функции f (x) на данном промежутке, если для любого х из данного промежутка F'(x)= f (x). Основное свойство первообразных. Если F (x) – первообразная функции f (x), то и функция F (x)+ C , где C –произвольная постоянная, также является первообразной функции f (x) (т.е. все первообразные функции f(x) записываются в виде F(x) + С ).
Геометрическая интерпретация. Графики всех первообразных данной функции f (x) получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси Оу.
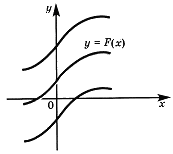
Таблица первообразных.
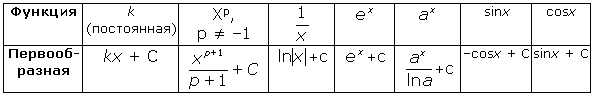
Правила нахождения первообразных . Пусть F(x) и G(x) – первообразные соответственно функций f(x) и g(x). Тогда:
1. F ( x ) ± G ( x ) – первообразная для f ( x ) ± g ( x );
2. а F ( x ) – первообразная для а f ( x );
3. 
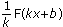– первообразная для а f ( kx + b ).
❷Конусом называется тело, состоящее из основания, точки не лежащей на основании (вершина конуса), и всех отрезков соединяющих вершину конуса с точками основания (образующая). Высотой конуса называется перпендикуляр опущенный из вершины конуса к основанию ( Sбоковое= ПRL). Усеченным конусом называется тело, заключенное между двумя основаниями. (Sбоковое= П (R1+R2) ×L .
Билет№5
1)Неопределенный интеграл и его свойства: Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функции f(x) и обозначается как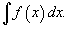 
Таким образом, если F - некоторая частная первообразная, то справедливо выражение
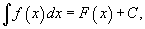где С - произвольная постоянная.
Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f,
а, k, C - постоянные величины.
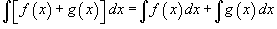
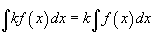
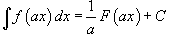
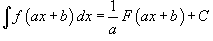
Усеченный конус. Конус.
Конус – тело состоящее из основани, точки не лежащей на основании(вершина конуса) и всех отрезков соединяющих вершину конуса с точками основания.(образующие)
Высотой конуса называют перпендикуляр опущенный из вершины к основанию.
Усеченный конус- тело заключенное между 2 мя основаниями.
Sбок=ПRL
Sбок.усечен.= П(R1 +R2)L
Билет№6
1) Показательная и логарифмическая функция ,свойства и графики: Показательная функция, такая функция, которая может быть задана формулой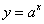 
, где а - любое положительное число, не равное единице.