Формальная и содержательная аксиоматики, аксиоматические теории и математические структуры.

Пусть R(T) - реализация некоторой системы аксиом Т или, что тоже, реализация структуры и теории определяемой этой системой аксиом. Рассмотрим подробнее, что означает эта реализация. Согласно определению реализации, данному в предыдущем П.6.3, реализация R(T) содержит:

1. объекты R_i (Q_i), являющиеся реализациями базовых объектов Q₁…, Q_m и обладающие таким свойством, что существует взаимно-однозначное соответствие R_i r_i(Q_i) между объектами Q_i и объектами R_i, i = 1,2,…,m;

2. отношения p_i(R₁,…, R_m), которые представляют в реализации R(T) отношения P_i(P₁,…,P_m) заданные системой аксиом для соответствующих объектов Q;

3 все утверждения, получаемые логическим следствием в теории данной системы аксиом входят в реализацию R(T) так же в виде некоторых утверждений , выраженных через отношения реализаций базовых объектов.

Рассмотрим пример.

Пусть R² - арифметическая модель евклидовой плоскости, тогда базовое множество М₁ - это все точки M R², реализующиеся в виде упорядоченных числовых пар (x,y). Базовое множество М₂ - это множество всех прямых l R², реализующихся уравнениями вида ax+by+c = 0. Отношение P₁(M,l) (M 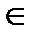l) , состоящее в том, точка М принадлежит прямой l, реализуется свойством P₁: пара (x,y) удовлетворяет уравнению ax+by+c = 0, и т.д.

Вывод 1.

Всякая реализация R(T) системы аксиом Т устанавливает взаимно однозначное соответствие R_i 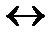r_i(Q_i) между базовыми объектами Q_i и объектами R_i реализаций Q_i в R(T) . При этом отношения P(P₁,…,P_m) заданные в системе аксиом Т реализуются некоторыми отношениями p (R_i,…, R_m) между соответствующими объектами R_i в R(T) .

Вывод 2.

Всякое утверждение в виде отношений объектов в теории Т 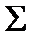, которое получается логическим следствием, выполняется и в реализации R(T) в виде некоторого свойства реализованных объектов. Таким образом, существует взаимно-однозначное соответствие между утверждениями теории Т 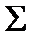, и выполнением соответствующих им свойств в реализации R(T).

Изначально структуру можно строить безотносительно её реализации.

Определение.

Система аксиом Т, ее аксиоматическая теория Т 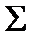и аксиоматическая структура 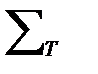определенные вне какой-либо реализации называются абстрактными или формальными системой аксиом, теорий или структурой соответственно.

Если существует реализация R(T) системы аксиом Т, её теории и её структуры, то система Т, её теория Т 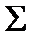и структура 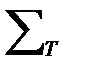называются содержательными.

Классическим примером формальной теории является мыслимая геометрия, построенная Н.И. Лобачевским. Эта мыслимая геометрия долгое время не воспринималась однозначно как содержательная аксиоматическая теория, пока не были найдены ее реализации, например, реализация Пуанкаре L₂, построенная нами выше. Таким образом, исторический опыт с геометрией Лобачевского имеет "хороший конец": были найдены реализации этой геометрии, и абстрактное аксиоматическое построение неевклидовой плоскости Лобачевского стало содержательной теорией.

История науки знает немало примеров, когда построенные теории так и не нашли соответствующих реализаций. Это касается не только теорий в математике, физике и других естественных науках, но и теорий экономических и социальных.

Изоморфизм.

В следующем параграфе мы покажем, как используются реализации для исследования свойств аксиоматических систем и теорий. Для этого нам потребуется ещё одно понятие - изоморфизм моделей аксиоматических структур.

Пусть система аксиом Т имеет две реализации R(T) и R^'(T). Тогда, согласно выводу 1, п.6.4, между реализациями R_i и R^'_i базовых объектов Q_i устанавливается взаимно-однозначное соответствие:

R_i ˂=> Q_i ˂=> R^'_i (6.2)

Это соответствие является отношением эквивалентности. Что можно сказать о соответствии между реализациями отношений Р_i в R_i и реализациями этих же отношений P^'_i в R^'_i ? Рассмотрим два примера.

Пример 1.

Пусть система аксиом Т состоит из 14 аксиом аксиоматики Гильберта, определяющих абсолютную геометрию плоскости (геометрию без аксиомы параллельности). Мы имеем две реализации этой планиметрии:

(1) - арифметическая модель R² (евклидовой плоскости);

(2) - модель Пуанкаре L₂ (плоскости Лобачевского). Можно установить взаимно однозначное соответствие между точками М 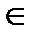R² и точками N 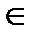L₂, а также установить некоторое соответствие между прямыми l 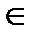R² и прямыми a 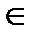L₂. В то же время не всем отношениям между точками и прямыми в модели L₂ можно найти соответствующие отношения в модели R². Например, отношение P(a₁, a₂, a₃,) 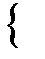прямые a_1, a₂ и a₃ не пересекаются в конечной части плоскости 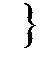может так выполняться в L_2, что не иметь аналога в R², (см. Рис.5.4 (а), §5).

Пример 2.

Пусть e² - геометрическая модель направленных отрезков (выполненная, например, карандашом на бумаге или реализованная на пиксельном экране компьютера). Пусть Е²- арифметическая модель векторного пространства. Операция откладывания вектора, указанная в модели Вейля, п.4.1, §4, устанавливает взаимно-однозначное отображение 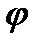: 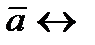(x,y) модели e²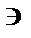 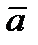на модель Е² 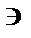(x,y). При этом, отображение 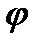сохраняет все определенные в векторной структуре отношения реализующимися между соответствующими векторам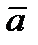и и 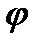( 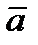)=(x,y).

Определение изоморфизма.

Две реализации R(T) и R'(T) системы аксиом Т будем называть изоморфными, если выполняется два условия:

1.Существует взаимно-однозначное соответствие (6.2) между реализациями R_i(Q_i) и R^'_i(Q_i) базовых объектов Q_i, i=1,2,…, m;

2. Отображение (6.2) устанавливает взаимно-однозначное соответствие между всеми отношениями p^'_i( R^'₁,…,R^'_m) и p_i(R₁,…, R_m), представляющими в моделях R^' и R^' определённые отношения P_i(Q₁,…, Q_m).

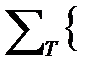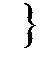Само отображение (6.2), при этом называется изоморфизмом моделей или изоморфизмом реализацией R(T) и R^'(T), а также изоморфизмом аксиоматических структур T;P;R и 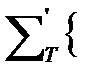T;P^';R^' .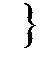