Свойства плотности вероятности

Плотность вероятности определена почти всюду. Если f является плотностью вероятности Свойства плотности вероятностиР

Интеграл от плотности по всему пространству равен единице:

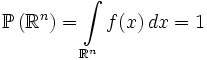Обратно, если f(x) — неотрицательная п.в. функция, такая что 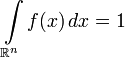, то существует абсолютно непрерывная вероятностная мера Рна 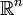такая, что f(x) является её плотностью.

Замена меры в интеграле Лебега:

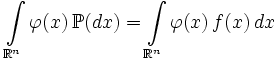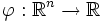где любая борелевская функция, интегрируемая относительно вероятностной меры Р.

Плотность случайной величины

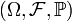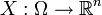Пусть определено произвольное вероятностное пространство , и случайная величина (или случайный вектор). X индуцирует вероятностную меру 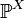на 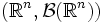, называемую распределением случайной величины X.

Определение 3. Если распределение 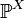абсолютно непрерывно относительно меры Лебега, то его плотность 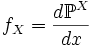называется плотностью случайной величины X. Сама случайная величина X называется абсолютно непрерывной.

Таким образом для абсолютно непрерывной случайной величины имеем: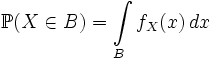

Замечания:Не всякая случайная величина абсолютно непрерывна. Любое дискретное распределение, например, не является абсолютно непрерывным относительно меры Лебега, а потому дискретные случайные величины не имеют плотности.

Функция распределения абсолютно непрерывной случайной величины X непрерывна и может быть выражена через плотность следующим образом:

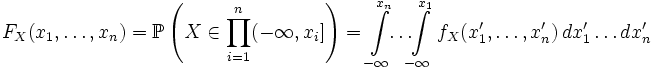
В одномерном случае

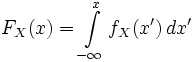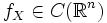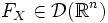Если , , то и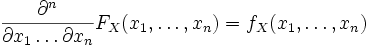

В одномерном случае: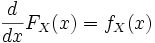

математическое ожидание функции от абсолютно непрерывной случайной величины может быть записано в ви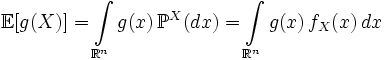де:

где 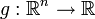— борелевская функция, так что 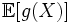определено и конечно.

Плотность преобразования случайной величины

Пусть 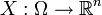— случайная величина, и 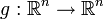— инъективная непрерывно дифференцируемая функция такая, что , 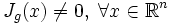где Jg(x) — якобиан функции g в точке x. Тогда случайная величина Y = g(X) также абсолютно непрерывна, и её плотность имеет вид:

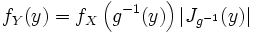
В одномерном случае:

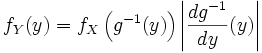
Теорема Чебышева

Теорема. Если Х1, Х2, …, Хn- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное число e, вероятность неравенства

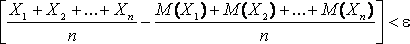
будет сколь угодно близка к единице, если число случайных величин достаточно велико.

Т.е. можно записать: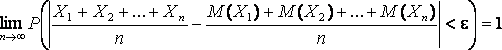

Часто бывает, что случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева несколько упрощается:

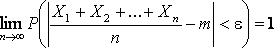
Дробь, входящая в записанное выше выражение есть не что иное как среднее арифметическое возможных значений случайной величины.

Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий.

Отклоняясь от математического ожидания как в положительную так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются.

Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности.