Возрастающие и убывающие последовательности называются монотонными последовательностями.

5. Предел числовой последовательности. Геометрический смысл.
Последовательность – это функция натурального аргумента.
Пример: числовые последовательности:
1) 1,2,…,n,…;
2) 1,-1,-1,…,(-1)^n,…,
3) 1, ½, 1/3,…,1/n,…
Число a называется пределом последовательности {Xn}, если ∀>∃n ∈N такой, что при всех выполняется неравенство: |Xn-a|< ε

В этом случае пишут: limXn, n →¥ =a В определении n0 зависит от ε:n0=n0(ε) Причем, с уменьшением ε соответствующий номер увеличивается.

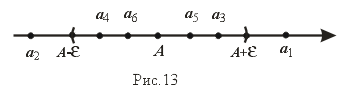
Геометрический смысл определения. Неравенство 2 равносильно двойному неравенству:a-ε<Xn<a+ ε,которое показывает, что элементXnнаходится в ε-окрестности точки a.
Сформулируем определение геометрически: Число a называется пределом последовательности {Xn}, если для любой ε-окрестности точки a найдется номер такой, что все значения Xn, для которых n>n0, попадут в ε-окрестность точки a. Внутри ε-окрестности точки a находится бесконечное число членов последовательности, а вне ее – лишь конечное их число.

6. Предел функции в точке. Геометрический смысл. Односторонние пределы. Бесконечно малые функции. Основные теоремы.
1)Число А называется пределом функции y=f(x) в точке x0, если для любой последовательности допустимых значений x(n) (x(n) <> х0), сходящейся к точке х0, последовательность соответствующих значений сходится к числу А.
2)Число А называется пределом функции y=f(x) в точке x0, если для любого положительного числа ε найдётся такое положительное число Δ, что для всех х, отличных от х0, и удовлетворяющих неравенству |x-x0|<Δ, будет выполняться неравенство |f(x)-A|<ε
Замечание:
Запись х<>х0 вместе с неравенством |x-x0|<Δ означает, что определение сформулировано для проколотой Δ-окрестности.
3)Число А называется пределом функции y=f(x), при х->+∞, если
1) функция определена на +∞
2) если для любого неотрицательного числа ε, найдётся такое число М, зависящее от ε, что, при всех х>М (ε), будет выполняться неравенство |f(x)-A|<ε.
4)Число А называется пределом функции y=f(x), при х->+∞, если
1) функция определена на -∞
2) если для любого неотрицательного числа ε, найдётся такое число М, зависящее от ε, что, при всех х<М (ε), будет выполняться неравенство |f(x)-A|<ε. Функция называется бесконечно малой в точке a или при x → a, если limx → af(x) = 0

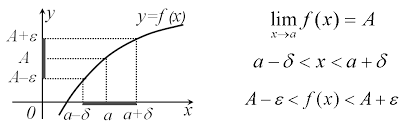Геометрический смысл предела функции в точке. Выясним, в чем заключается геометрический смысл предела функции в точке. Построим график функции y=f(x) и отметим на нем точки x=a и y=A
Предел функции y=f(x) в точке x→aсуществует и равен A, если для любой ε-окрестности точки A можно указать такую δ-окрестность точки a, что для любого x из этой δ-окрестности значение f(x) будет находиться в ε-окрестности точки A.
Отметим, что по определению предела функции в точке для существования предела при x → a не важно, какое значение принимает функция в самой точке a. Можно привести примеры, когда функция не определена при x=a или принимает значение, отличное от A. Тем не менее, предел может быть равен A

Односторонним пределом функции называется предел справа или предел слева.
Пределом функции f(x) в точке x=a слева называется предел, вычисляемый в предположении, что x → a, оставаясь все время меньше значения a. Аналогично, пределом справа называется предел функцииf(x) при x → a, при том, что x> a. Односторонние пределы обозначаются так: limf(x), x → a-0 и limf(x), x → a+0

Функция y=a(x) называется бесконечно малой величиной при x → a (или при x → ∞), если ее предел равен нулю.

Пример: при x → 3, функция f(x)=x-3 бесконечно мала