Понятие числовой последовательности. Ограниченные и монотонные последовательности.

Понятие числовой последовательности. Ограниченные и монотонные последовательности.

Пусть каждому натуральному числу n поставлено в соответствие некоторое единственное действительное число (при этом разным натуральным числам n могут соответствовать и одинаковые действительные числа). В этом случае на множестве натуральных чисел определена функция: , которая называется числовой последовательностью или просто последовательностью.

Последовательность обозначается: , n=1, 2,… или .

Числа , ,… называются членами последовательности или ее элементами, – общим членом последовательности, n – номером члена .

По определению любая последовательность содержит бесконечное множество элементов.

Ограниченные последовательности: Последовательность аn называется ограниченной, если для любого n ∈ N существуютчисла m M(соответственно нижняя и верхняя границы последовательности) такие, что выполняется неравенство m<an< M.

Монотонные последовательности: Последовательность аn=f(n) называется возрастающей(неубывающей), если аn<an+1(an<an+1) для любого n ∈ N, иубывающей(невозрастающей) , если an>an+1 (an>an+1) для любого n ∈ N .

Теория. Единственность предела функции. Функция не может иметь в одной точке два различных предела.

Предел суммы двух функции. Предел суммы двух функций равен сумме пределов: lim(f(x)+g(x))=limf(x)+limg(x),
x → a
Предел произведения двух функции. Предел произведения двух функций равен произведению пределов: lim(f(x)*g(x))=limf(x)*limg(x), x → a
Предел частного двух функции. Предел частного двух функций равен частному пределов, если предел делителя не равен нулю: limf(x)/g(x)=limf(x)/limg(x), x → a
Теорема о двух милиционерах для функции). Если в некоторой окрестности точки x=a функция f(x) заключена между двумя другими функциями g(x) и f(x), имеющими один тот же предел A при x→a:

g(x) ≤f(x) ≤h(x), limg(x)=limh(x)=A, x → a

Теоремы:
1. Предел константы равен самой этой константе: с = с.

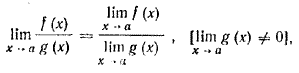
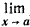
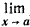
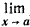
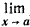
2. Постоянный множитель можно выносить за знак предела:
[k • f (х)] = k • 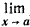f (х).
3. Предел суммы (разности) функций равен сумме (разности) пределов этих функций:
[ f (х) ± g (х)] = 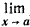f (х) ± 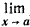g (x).
4. Предел произведения функций равен произведению пределов этих функций:
[ f (х) • g (х)] = 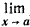f (х) • 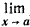g (x).
5. Предел отношения двух функций равен отношению пределов этих функций, если только предел делителя не равен нулю:

7. Cвойства пределов последовательности
1)Предел суммы равен сумме пределов, если каждый из них существует, т.е.

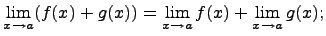
Предел разности равен разности пределов, если каждый из них существует, т.е.

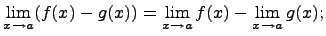
3)Предел постоянной величины равен самой постоянной величине:

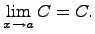
4)Предел произведения функции на постоянную величину.Постоянныйкоэффициэнт можно выносить за знак предела:

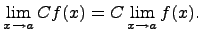
Предел произведения. Предел произведения равен произведению пределов, если каждый из них существует, т.е.

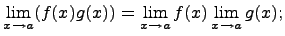
Предел частного.Предел частного равен частному пределов, если каждый из них существует и знаменатель не обращается в нуль, т.е.

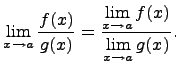
Предел степенной функции

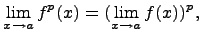
Второй замечательный предел

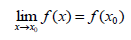
10. Определение непрерывности в точке, в интервале, на отрезке. Точки разрыва первого и второго рода.
Опр.1 Функция y=f(x) называется непрерывной в точке x0 если она определена в этой точке и в некоторой её окрестности и:

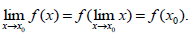
Так как limx=x0, x->x0, то равенство 1 можно записать в виде:

Геометрически теорема Ферма означает, что в точках наибольшего или наименьшего значений дифференцируемой функции касательная к графику функции имеет нулевой угловой коэффициент, т.е. параллельна оси Ох.

Максимум и минимум функции

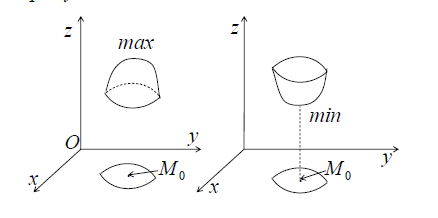
Пусть функция z=f(x;y) определена в некоторой области D иM0(x0;y0)ÎD
Опр.1 ТочкаM0(x0;y0) называется точкой максимумафункции z=f(x;y), если существует такая δ-окрестностьэтой точки, что для каждой точки M¹M0из этойокрестности выполняется неравенство: f(x;y) <f(x0;y0)
Опр.2 Точка M0(x0;y0) называется точкой минимумафункции z=f(x;y), если существует такая δ-окрестностьэтой точки, что для каждой точки M¹M0из этойокрестности выполняется неравенство: f(x;y) >f(x0;y0)
Значение функции z=f(x;y) в точке максимума(минимума) называется максимумом (минимумом)функции. Максимум и минимум функции называют ееэкстремумами.
Замечание1: В силу определения, точка экстремумалежит внутри области определения функции.Максимум и минимум имеют локальный (местный)характер: значение функции в точкеM0(x0;y0)сравнивается с ее значениями в точках, достаточноблизких к (x0;y0)
В области D функция может иметь несколько экстремумов или не иметь ни одного.

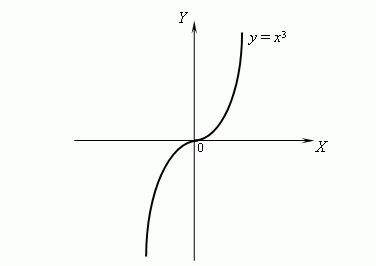27. Выпуклость и вогнутость кривой. Точки перегиба.
Если производная f ' ( x ) функции f ( x ) дифференцируема в точке ( x0 ), то её производная называется второй производной функции f ( x ) в точке ( x0 ), и обозначается f '' ( x0 ).
Функция f ( x ) называется выпуклой на интервале ( a, b ), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 ) ), x0 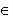( a, b ).
Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 ) ), x0 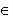( a, b ).
Достаточное условие вогнутости ( выпуклости )функции.Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:если f '' ( x ) > 0 для любого x 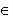( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );
если f '' ( x ) < 0 для любого x 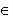( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0.
Рассмотрим график функции y = x3

Эта функция является вогнутой при x > 0 и выпуклой при x < 0. В самом деле, y'' = 6x, но 6x> 0 при x > 0 и 6x < 0 при x < 0, следовательно, y'' > 0 при x > 0 и y'' < 0 при x < 0, откуда следует, что функция y = x3является вогнутой при x > 0 и выпуклой при x < 0. Тогда x = 0 является точкой перегиба функции y = x3.

28. Асимптоты графика функций

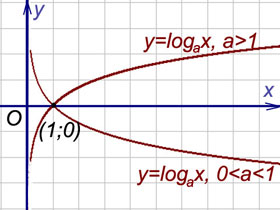
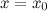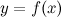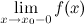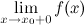Прямая называется вертикальной асимптотой графика функции , если хотя бы одно из предельных значений или равно 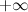или .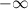

Замечание. Прямая 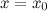не может быть вертикальной асимптотой, если функция непрерывна в точке 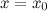. Поэтому вертикальные асимптоты следует искать в точках разрыва функции.

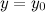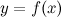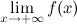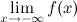Прямая называется горизонтальной асимптотой графика функции , если хотя бы одно из предельных значений или равно .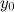

Формула Ньютона-Лейбница

Метод вариации постоянной

Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения:

y′+a(x)y=0.
Общее решение однородного уравнения содержит постоянную интегрирования C. Далее мы заменяем константу C на некоторую (пока еще неизвестную) функцию C(x). Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию C(x).

38. Уравнения Бернулли.

Уравнение Бернулли является одним из наиболее известных нелинейных дифференциальных уравнений первого порядка. Оно записывается в видеy′+a(x)y=b(x)ym,где a(x) и b(x) − непрерывные функции.
Если m=0, то уравнение Бернулли становится линейным дифференциальным уравнением. В случае когда m=1, уравнение преобразуется в уравнение с разделяющимися переменными. В общем случае, когда m≠0,1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановкиz=y1−m.
Новое дифференциальное уравнение для функции z(x) имеет видz′+(1−m)a(x)z=(1−m)b(x).

По определению,

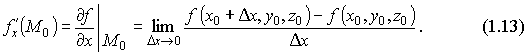
Частные производные по y и по z определяются аналогично:

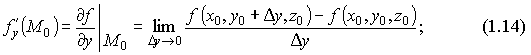
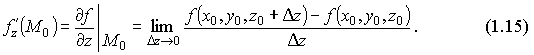
Производные f'_x, f'_y, f'_z называются ещё и частными производными первого порядка функции f(x,y,z), или первыми частными производными.

Так как частное приращение Δxf(M₀) получается лишь за счет приращения независимой переменной x при фиксированных значениях других независимых переменных, то частная производная f'_x(M₀) может рассматриваться как производная функции f(x,y₀,z₀) одного переменного x. Следовательно, чтобы найти производную по x, нужно все остальные независимые переменные считать постоянными и вычислять производную по x как от функции одного независимого переменного x.

Рассмотрим функцию z=f(х,у) двух независимых переменных и установим геометрический смысл частных переменных z'_x=f'_x(х,у) и z'_y=f'_y(х,у).

В этом случае уравнение z=f(х,у) есть уравнение некоторой поверхности (рис.1.3). Проведем плоскость y = const. В сечении этой плоскостью поверхности z=f(х,у) получится некоторая линия l₁ пересечения, вдоль которой изменяются лишь величины х и z.

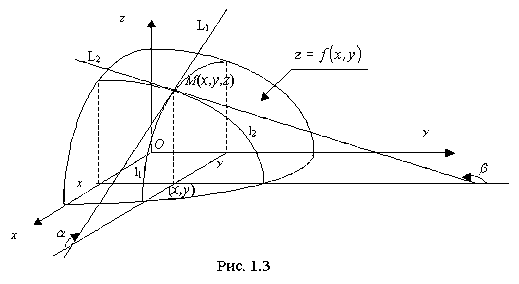
Частная производная z'_x (её геометрический смысл непосредственно следует из известного нам геометрического смысла производной функции одной переменной) численно равна тангенсу угла α наклона, по отношению к оси Ох , касательной L₁ к кривой l₁, получающейся в сечении поверхности z=f(х,у) плоскостью y = const в точке М(х,у,f(xy)): z'_x= tgα.

В сечении же поверхности z=f(х,у) плоскостью х = const получится линия пересечения l₂, вдоль которой изменяются лишь величины у и z. Тогда частная производная z'_y численно равна тангенсу угла β наклона по отношению к оси Оу, касательной L₂ к указанной линии l₂пересечения в точке М(х,у,f(xy)): z'_x= tgβ.

Понятие числовой последовательности. Ограниченные и монотонные последовательности.

Пусть каждому натуральному числу n поставлено в соответствие некоторое единственное действительное число (при этом разным натуральным числам n могут соответствовать и одинаковые действительные числа). В этом случае на множестве натуральных чисел определена функция: , которая называется числовой последовательностью или просто последовательностью.

Последовательность обозначается: , n=1, 2,… или .

Числа , ,… называются членами последовательности или ее элементами, – общим членом последовательности, n – номером члена .