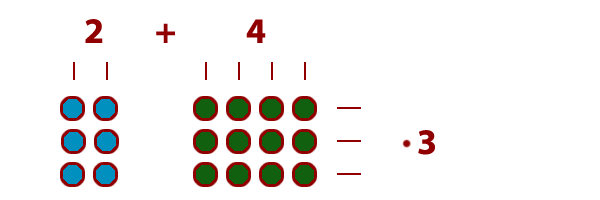
 Рассмотрим два выражения: ( 2 + 4 ) • 3 и 2 • 3 + 4 • 3 Оба выражения равны 18 : ( 2 + 4 ) • 3 = 6 • 3 = 18 ; 2 • 3 + 4 • 3 = 6 + 12 = 18 . Получается, что: ( 2 + 4 ) • 3 = 2 • 3 + 4 • 3 . Для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения. Это правило называется распределительным свойством умножения относительно сложения. С помощью букв его записывают так: ( a + b ) • c = a • c + b • c . |
| Также это правило применимо к разности, умноженной на число: ( a – b ) • c = a • c – b • c , и называется оно распределительным свойством умножения относительно вычитания. Например: ( 5 – 3 ) • 7 = 5 • 7 – 3 • 7 |
| Используя распределительное свойство умножения можно упрощать буквенные выражения. Например: 3a + 5a = 3 • a + 5 • a = ( 3 + 5 ) • a = 8a ; 4b + b = 4 • b + 1 • b = ( 4 + 1 ) • b = 5b ; 9c – 5c = 9 • c – 5 • c = ( 9 – 5 ) • c = 4c . |
| Также для упрощения выражений можно применять сочетательное свойство умножения: 3х • 4 • 5 = ( 3 • 4 • 5 ) • х = 60х . |
Степень числа. Квадрат и куб числа. Правила
| Мы уже знаем что, для выражений вида 5 + 5 + 5 + 5 существует более короткая запись 5 • 4 . Аналогично сумме с одинаковыми слагаемыми, для произведения с одинаковыми множителями существует короткая запись. Например: 2 • 2 • 2 • 2 = 2 4 . Запись 2 4 читается так, два в четвертой степени, и обозначает произведение четырех множителей, каждый из которых равен двум. 2 называется основанием степени и показывает, чему равны множители в произведении. 4 — показатель степени, показывает, сколько множителей в произведении. |
| Примеры: 4 • 4 • 4 = 4 3 = 64 ; 7 • 7 • 7 • 7 = 7 4 = 2401 ; 2 • 2 • 2 • 2 • 2 = 2 5 = 32 . |
| Число во второй степени a 2 = a • a называют число в квадрате (в данном случае a в квадрате). Число в третьей степени x 3 = x • x • x называют число в кубе (в данном случае x в кубе). |
| Степени чисел входящие в числовые выражения выполняются в первую очередь. 2 3 + 4 2 = 8 + 16 = 24 ; 2 2 • 3 2 = 4 • 9 = 36 . Знак степени стоящий сразу за скобками предполагает произвести вычисления в скобках, а затем полученный результат возвести в степень. (2+4) 2 = 6 2 = 36 . |
| Формулы скорости, площади и объема |
 15. Формулы. Формула скорости, пути |
 16. Площадь. Формула площади прямоугольника |
| 17. Прямоугольный параллелепипед. Объем |
Формулы. Формула скорости, пути. Правила
| Скорость это физическая величина, показывающая, какое расстояние пройдет объект за единицу времени. Скорость90 км/ч. обозначает, что объект за один час преодолеет 90 км. Давайте напишем формулу скорости. Формула это математическая запись, в которой величины представлены в виде общепринятых букв (переменных). Скорость — V Путь — S Время — t Исходя из этого, формула скорости будет выглядеть так: V = S : t Применим эту формулу для решения следующей задачи. Машина, двигаясь равномерно (с постоянной скоростью) за два часа прошла 120 км. С какой скоростью двигалась машина? V = S : t = 120 : 2 = 60 км/ч. Мы подставили в формулу пройденное расстояние (путь) и время за которое оно было пройдено, и нашли скорость. V = 60 км/ч. |
| Теперь, исходя из формулы скорости, напишем формулу пути. S = V • t Решим задачу. Поезд двигался равномерно 3 часа со скоростью 50 километров в час. Какой путь прошел поезд за это время? S = V • t = 50 • 3 = 150 км. Используя формулу пути, мы нашли ответ. Поезд за 3 часа прошел 150 километров. |
Наши рекомендации
