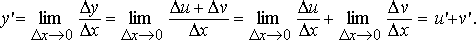Непрерывность функции. Точки разрыва
Непрерывность функции. Точки разрыва
1.Непрерывность функции в точке
Непрерывная функция — функция без «скачков», то есть такая, у которой сколь угодно малые изменения аргумента приводят к сколь угодно малым изменениям значения функции.
Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
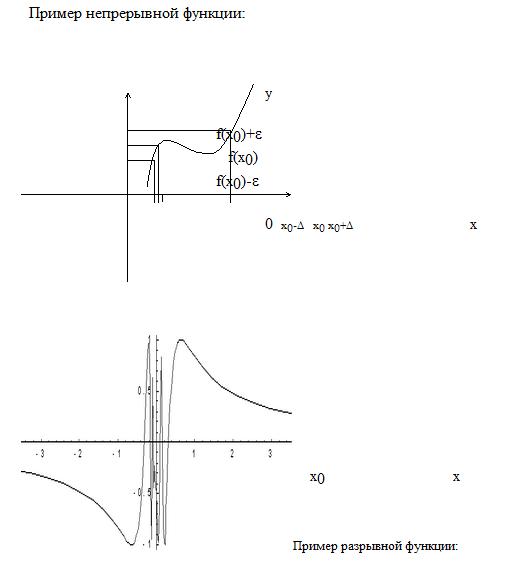
Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих условию
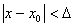
верно неравенство 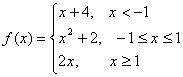 .
.
Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
f(x) = f(x0) + (x)
где (х) – бесконечно малая при хх0.
 2. Точка разрыва функции
2. Точка разрыва функции
 1. Теорема о непрерывности функции в точке
1. Теорема о непрерывности функции в точке

3.Теорема о непрерывности обратной функции
Пусть y = f(x) - функция с областью определения X (D(f) = X) и областью значений Y (E(f) = Y). При этом разным значениям х отвечают разные значения y. Тогда для каждого значения y Î Y существует только одно x Î Х, такое , что f(x) = y. Если мы сопоставим каждому y Î Y именно такое x, то получим отображение множества Y в множество X. Это отображение называется обратным к данному отображению f и обозначается f -1 , т. е. обратная функция для y = f(x) есть x = f –1(y). Пусть y = f(x) (x Î D (f)) непрерывна и возрастает на отрезке [a; b], тогда обратная функция x = f—1(y) также непрерывна и возрастает на [f(a); f(b)]. (аналогично для непрерывной убывающей функции).
18. Односторонняя непрерывность. Точки разрыва, их 7классификация. Функция , определённая в некоторой окрестности точки х0, называется непрерывной в этой точке, если предел функции в точке х0 существует и равен значению в этой точке. Функция f(x), определённая на отрезке [a,b], называется непрерывной в точке а справа, если lim f(x)=f(a) (аналогично слева)
x®a+0
Функция y=f(x) непрерывна на Х, если эта функция непрерывна в каждой точке этого промежутка.
Если lim f(x) не равен lim f(x0)
X®Xo ,то х0 - точка разрыва непрерывности этой функции.
Классификация точек разрыва.
1. х0 – точка разрыва первого рода, если одосторонние пределы существуют, но они не равны между собой.
1.1 Точка устранимого разрыва, если односторонние пределы равны между собой, но их значение не совпадает со значением функции в этой точке.
Lim f(x)=lim f(x) не равен f(x0)
X®Xo-0 X®Xo+0
1.2 Точка разрыва с «конечным скачком». Правый и левый пределы не совпадают.
1.3 Точка разрыва с «бесконечным скачком». Хотя бы один односторонних
пределов бесконечен.
2. х0 - точка разрыва второго рода, если хотя бы один из
односторонних пределов не существует.
 4. Теорема о сохранении знака непрерывной функции
4. Теорема о сохранении знака непрерывной функции
2)Производная функции. Правила вычисления производных. Таблицы производных.
1)Касательная к кривой
Уравнение касательной
Пусть функция задается уравнением y=f(x), нужно написать уравнение касательнойв точке x0. Из определения производной:
y/(x)=limΔx→0ΔyΔx
Δy=f(x+Δx)−f(x).
Уравнение касательнойк графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k
Т.к. x0 и f(x0)∈ прямой, то уравнение касательнойзаписывается в виде: y−f(x0)=f/(x0)(x−x0), или
y=f/(x0)·x+f(x0)−f/(x0)·x0.
2) Производная функция в точке Предел отношения приращения функции Δy к его приращению независимой переменной Δx, при стремлении Δx к нулю, то есть limΔx→0ΔxΔy=limΔx→0Δxf(x0+Δx)−f(x0), называетсяпроизводной функции y=f(x) пo независимой переменной x, при данном ее значении (или в данной точке) x=x0.т получаем производну и в полученную функцию подставляем координаты х.
3)механический смысл производной. Производная пути по времени есть скорость. Производная скорости по времени или вторая производная пути по времени есть ускорение.
4) Геометрический смысл производной.производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
5)Нормаль к кривой
Уравнение нормали
Нормаль-- это перпендикуляр к касательной(см. рисунок). Исходя из этого:
tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)
Т.к. угол наклона нормали -- это угол β1, то имеем:
tgβ1=tg(π−β)=−tgβ=−1f/(x).
Точка (x0,f(x0))∈ нормали, уравнение примет вид:
y−f(x0)=−1f/(x0)(x−x0).
6) Логарифмическая производная
Логарифмическая производная– производная от натурального логарифма модуля (абсолютной величины) – данной функции: 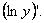
Используя формулу производной сложной функции, найдем, что
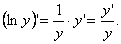 (*)
(*)
Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции.
ТЕОРЕМЫ МАТИХ ЕТИ!
1)Вывести уравнение касательной и нормали к кривой: уравнение касательной можно привести к виду y=kx+b . Вспомним, что угловой коэффициент прямой kравен тангенсу угла наклона прямой к положительному направлению оси Ох или значению производной функции в точке проведения касательной , т.е. y=f `(хо )· x+b.
Для вычисления воспользуемся тем, что касательная проходит через точку А(xo ; f(xo )), т.е. f(xo )=f ´(xo )·x +b,т.е. b = f(xo ) – f ´(xo )·x ,т.е.
y=f `(хо )· x+ f(xo ) – f ´(xo )·x, после преобразований имеем:
y = f(xo) + f ´(xo ) · (x – xo )
нормаль смотреть в определениях
2) Рассмотрим следующие вопросы, который касаются функций.
Если функция непрерывна, то она дифференцируема?
Если функция дифференцируема, то она непрерывна?
Ответ на первый вопрос: из непрерывности функции не следует ее дифференцируемость.
Ответ на второй вопрос: из дифференцируемости функции следует ее непрерывность.
Рассмотрим более конкретно каждый вопрос. Чтобы ответить на данные вопросы необходимо доказать озвученый факт или привести пример, который опровергает этот факт.
Найдем производную следующей функции 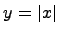 . Хорошо известно, данная функция является непрерывной и, что ее производная будет следующей:
. Хорошо известно, данная функция является непрерывной и, что ее производная будет следующей:
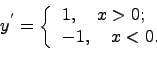
Покажем, что в точке нуль производная не существут. Для этого найдем производную в нуле по определению производной:
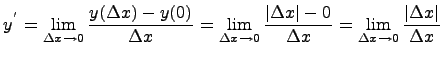
данный предел равен 1, если 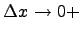 и равен (-1), если
и равен (-1), если 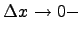 , получаем, что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема.
, получаем, что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема.
Если y = c, где c = const, то y' = 0.
Доказательство
Функция y = c принимает значение, равное c для любого аргумента x. Таким образом, Δy = 0при любомx. Следовательно,
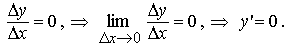
Теорема доказана.
Теорема
3. Пусть функции u = u(x), v= v(x) дифференцируемы. Тогда 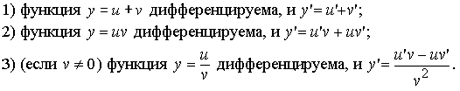
Доказательство
Если аргумент x получит приращение Δx, то функции u, v получат приращения
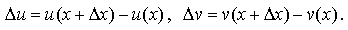
Пусть y = u + v, тогда
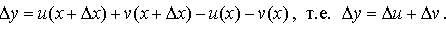
Воспользовавшись свойством предела суммы функции, получаем
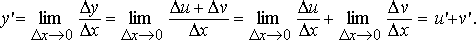
Доказательство
Если аргумент x получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x). С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом:Δx=g(y + Δy) − g(y).
Тогда получаем
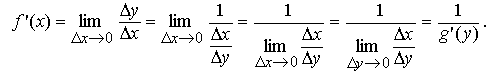
Теорема доказана.
Дифференциал функции.
1. Дифференциал функции в точке.

1. Правила дифференцирования

2. Применение дифференциала к приближенным вычислениям


Комплексныечисла
Определения:
1) Комплексное число - расширение множества вещественных чисел, обычно обозначается 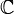 . Любое комплексное число может быть представлено как формальная сумма
. Любое комплексное число может быть представлено как формальная сумма 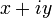 , где
, где 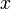 и
и 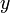 — вещественные числа,
— вещественные числа, 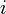 — мнимая единица.
— мнимая единица.
2) Запись комплексного числа 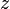 в виде
в виде 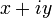 ,
, 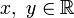 , называется алгебраической формой комплексного числа.
, называется алгебраической формой комплексного числа.
3) Угол 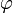 (в радианах) радиус-вектора точки, соответствующей числу
(в радианах) радиус-вектора точки, соответствующей числу 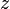 , называется аргументом числа
, называется аргументом числа 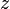 и обозначается
и обозначается 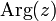 .
.
4) Модулем комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).
Модуль комплексного числа 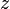 обозначается
обозначается 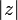 и определяется выражением
и определяется выражением 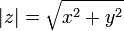 . Часто обозначается буквами
. Часто обозначается буквами  или
или 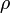 . Если
. Если 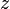 является вещественным числом, то
является вещественным числом, то 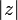 совпадает с абсолютной величиной этого вещественного числа.
совпадает с абсолютной величиной этого вещественного числа.
5) Если комплексное число 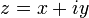 , то число
, то число 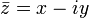 называется сопряжённым (или комплексно сопряжённым) к
называется сопряжённым (или комплексно сопряжённым) к 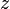 (обозначается также
(обозначается также 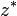 ). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.
). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.
6) Если вещественную 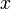 и мнимую
и мнимую 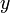 части комплексного числа выразить через модуль
части комплексного числа выразить через модуль 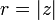 и аргумент
и аргумент 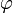 (
( 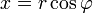 ,
, 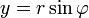 ), то всякое комплексное число
), то всякое комплексное число 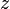 , кроме нуля, можно записать в тригонометрической форме
, кроме нуля, можно записать в тригонометрической форме
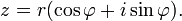
7) Опреденеиепроизведения комплексных чисел устанавливается с таким расчетом, чтобы числа a + b·i и a′ + b′·i можно было перемножать как алгебраические двухчлены, и чтобы число i обладало свойством i2=−1.
8) Пусть 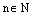 – произвольное натуральное число. Корнем n-ой степени из комплексного числа z называется комплексное число
– произвольное натуральное число. Корнем n-ой степени из комплексного числа z называется комплексное число 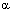 , такое, что
, такое, что 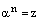 .
.
9) Показательнаяформа записи комплексных чисел
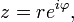 где
где 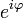 — расширение экспоненты для случая комплексного показателя степени.
— расширение экспоненты для случая комплексного показателя степени.
Свойства и теоремы:
1) Произведением двух комплексных чисел в алгебраической форме называется такое комплексное число, модуль которого равен произведению модулей сомножителей, а аргумент – сумме аргументов сомножителей.
2) Для того, чтобы перемножить два комплексных числа в тригонометрической формезаписи нужно перемножить их модули, а аргументы сложить. Пусть 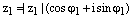 , где
, где 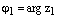 и
и 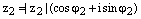 , где
, где 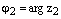 – два произвольных комплексных числа записанных в тригонометрической форме. Тогда
– два произвольных комплексных числа записанных в тригонометрической форме. Тогда 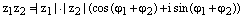 .
.
3) Формула Муавра для комплексных чисел 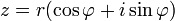 утверждает, что
утверждает, что 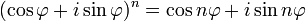 для любого
для любого 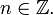
4) Для того, чтобы разделить комплексное число (a1 + b1i ) на другое комплексное число (a2 + b2i ), то есть найти 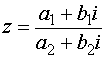 , нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.
, нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.
5) 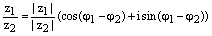
6) 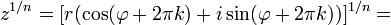
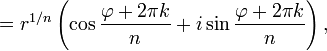
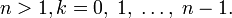
8.Интегральное исчисление функций одной переменной.
1) Первообразная
Функция F(x), дифференцируема на некотором интервале (а,b) называется первообразной для функции f(x) на этом интервале, если для каждого x 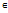 (a,b) справедливо равенство
(a,b) справедливо равенство
F´(x)=f(x)
2) Неопределенный интеграл
Если F(x) является первообразной для функции f(x) на некотором интервале, то выражение F(x)+C называется неопределенным интегралом от функции f(x) и обозначается 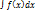
3) Определенный интеграл
Под определенным интегралом 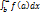 от данной функции f(x) на данном отрезке [a,b] понимается соответствующее приращение ее первообразной, т.е
от данной функции f(x) на данном отрезке [a,b] понимается соответствующее приращение ее первообразной, т.е
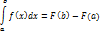
4) Несобственный интеграл от разрывной функции
Пусть функция f(x) непрерывна a ≤x≤b и имеет точку разрыва при x=b. Тогда соответствующий несобственный интеграл от разрывной функции определяется формулой
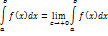
и называется сходящимся или расходящимся в зависимости от того, существует или не существует предел правой части равенства
5) Несобственный интеграл с бесконечным промежутком интегрирования
Пусть функция f(x) непрерывна при a≤x≤b+∞. Тогда по определению
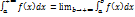 Если предел существует, то интеграл стоящий в левой части равенства, называется сходящимся и его значение определяется формулой; в противном случае равенство теряет смысл, интеграл стоящий слева, называется расходящимся и ему не приписывается никакого числового значения
Если предел существует, то интеграл стоящий в левой части равенства, называется сходящимся и его значение определяется формулой; в противном случае равенство теряет смысл, интеграл стоящий слева, называется расходящимся и ему не приписывается никакого числового значения
Свойства и теоремы
6) Формула интегрирования по частям в неопределенном интеграле
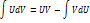
7) Сформулировать правила интегрирования дробно-рациональных функций
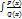 dx
dx
1. Делим числитель на знаменатель
2. Q(x) =(x- 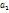 )(x-
)(x- 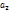 )…
)…
3. Раскладываем дробь на сумму простых дробей 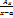 ;
; 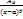 ;
; 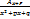 ;
; 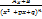 ;
;
1 2 3 4
Интеграл от дробей 1 и 2 типа вычисляется внесением функции под знак дифференциала, 3 и 4 сначала в знаменателе выделяется полный квадрат.
8) Сформулируйте правило интегрирования тригонометрических функций
1. 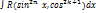
2. t=tg  dx=
dx= 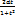
cosx = 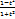 sinx=
sinx= 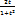
9) С формулировать свойства определенного интеграла
1. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е 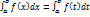
2. Определенный интеграл с одинаковыми пределами равен нулю 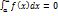
3. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный 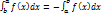
4. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутку [a,b] , равен сумме определенных интегралов, взятых по всем его частичным промежуткам 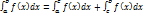
5. Постоянный множитель можно выносить за знак определенного интеграла 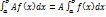
6. Определенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций 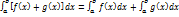
10) Формула Ньютона-Лейбница
Если f непрерывна на отрезке [a,b] и F- ее любая первообразная на этом отрезке, то имеет место равенство 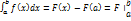
11) Формула интегрирования по частям в определенном интеграле
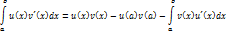
Для краткости употребляется обозначение 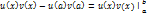
2) Сформулировать свойства неопределенного интеграла
1. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции
2. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянного слагаемого
3. Отличный от нуля постоянный множитель можно выносить за знак неопределенного интеграла
4. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме неопределенных интегралов от этих функций
5) Замена переменной в неопределенном интеграле
Пусть требуется найти интеграл 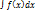 . Введем новую переменную t, положив x=
. Введем новую переменную t, положив x=  (t), где
(t), где  (t)- непрерывная функция с непрерывной производной, имеющая обратную функцию t=Ψ(t). Тогда
(t)- непрерывная функция с непрерывной производной, имеющая обратную функцию t=Ψ(t). Тогда 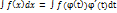 причем в правой части после интегрирования следует сделать подстановку t=Ψ(x)
причем в правой части после интегрирования следует сделать подстановку t=Ψ(x)
3) Таблица интегралов
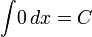
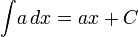
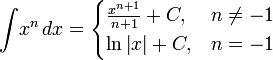
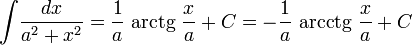
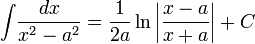
Логарифмы
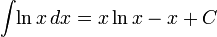
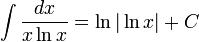
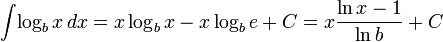
Экспоненциальные функции
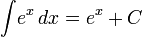
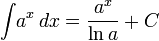
Иррациональные функции
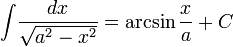
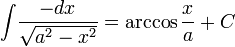
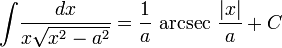
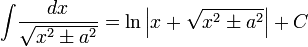
Тригонометрические функции
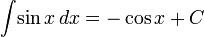
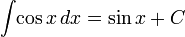
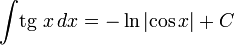
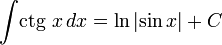
12) Замена переменной в определенном интеграле
Функция f(x) непрерывна на отрезке [a,b], функция x=  (t) имеет на отрезке [
(t) имеет на отрезке [ 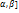 непрерывную производную, при этом a≤
непрерывную производную, при этом a≤ 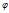 (t)≤b и
(t)≤b и 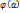 =а,
=а, 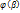 =b
=b
Тогда 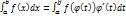
13) Вычисление площади плоской фигуры
Пусть функция f(x) непрерывна на отрезке [a,b]. Если при этом f(x)≥0 на [a,b], то площадь криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=a, x=b, выразится с помощью интеграла:
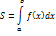
Если же f(x)≤0 на [a,b], то –f(x)≥0 на [a,b]. Поэтому площадь S соответствующей криволинейной трапеции находится по формуле
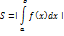
В полярных координатах 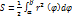
Непрерывность функции. Точки разрыва
1.Непрерывность функции в точке
Непрерывная функция — функция без «скачков», то есть такая, у которой сколь угодно малые изменения аргумента приводят к сколь угодно малым изменениям значения функции.
Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.

Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих условию
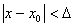
верно неравенство 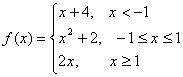 .
.
Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
f(x) = f(x0) + (x)
где (х) – бесконечно малая при хх0.
 2. Точка разрыва функции
2. Точка разрыва функции
 1. Теорема о непрерывности функции в точке
1. Теорема о непрерывности функции в точке

3.Теорема о непрерывности обратной функции
Пусть y = f(x) - функция с областью определения X (D(f) = X) и областью значений Y (E(f) = Y). При этом разным значениям х отвечают разные значения y. Тогда для каждого значения y Î Y существует только одно x Î Х, такое , что f(x) = y. Если мы сопоставим каждому y Î Y именно такое x, то получим отображение множества Y в множество X. Это отображение называется обратным к данному отображению f и обозначается f -1 , т. е. обратная функция для y = f(x) есть x = f –1(y). Пусть y = f(x) (x Î D (f)) непрерывна и возрастает на отрезке [a; b], тогда обратная функция x = f—1(y) также непрерывна и возрастает на [f(a); f(b)]. (аналогично для непрерывной убывающей функции).
18. Односторонняя непрерывность. Точки разрыва, их 7классификация. Функция , определённая в некоторой окрестности точки х0, называется непрерывной в этой точке, если предел функции в точке х0 существует и равен значению в этой точке. Функция f(x), определённая на отрезке [a,b], называется непрерывной в точке а справа, если lim f(x)=f(a) (аналогично слева)
x®a+0
Функция y=f(x) непрерывна на Х, если эта функция непрерывна в каждой точке этого промежутка.
Если lim f(x) не равен lim f(x0)
X®Xo ,то х0 - точка разрыва непрерывности этой функции.
Классификация точек разрыва.
1. х0 – точка разрыва первого рода, если одосторонние пределы существуют, но они не равны между собой.
1.1 Точка устранимого разрыва, если односторонние пределы равны между собой, но их значение не совпадает со значением функции в этой точке.
Lim f(x)=lim f(x) не равен f(x0)
X®Xo-0 X®Xo+0
1.2 Точка разрыва с «конечным скачком». Правый и левый пределы не совпадают.
1.3 Точка разрыва с «бесконечным скачком». Хотя бы один односторонних
пределов бесконечен.
2. х0 - точка разрыва второго рода, если хотя бы один из
односторонних пределов не существует.
 4. Теорема о сохранении знака непрерывной функции
4. Теорема о сохранении знака непрерывной функции
2)Производная функции. Правила вычисления производных. Таблицы производных.
1)Касательная к кривой
Уравнение касательной
Пусть функция задается уравнением y=f(x), нужно написать уравнение касательнойв точке x0. Из определения производной:
y/(x)=limΔx→0ΔyΔx
Δy=f(x+Δx)−f(x).
Уравнение касательнойк графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k
Т.к. x0 и f(x0)∈ прямой, то уравнение касательнойзаписывается в виде: y−f(x0)=f/(x0)(x−x0), или
y=f/(x0)·x+f(x0)−f/(x0)·x0.
2) Производная функция в точке Предел отношения приращения функции Δy к его приращению независимой переменной Δx, при стремлении Δx к нулю, то есть limΔx→0ΔxΔy=limΔx→0Δxf(x0+Δx)−f(x0), называетсяпроизводной функции y=f(x) пo независимой переменной x, при данном ее значении (или в данной точке) x=x0.т получаем производну и в полученную функцию подставляем координаты х.
3)механический смысл производной. Производная пути по времени есть скорость. Производная скорости по времени или вторая производная пути по времени есть ускорение.
4) Геометрический смысл производной.производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
5)Нормаль к кривой
Уравнение нормали
Нормаль-- это перпендикуляр к касательной(см. рисунок). Исходя из этого:
tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)
Т.к. угол наклона нормали -- это угол β1, то имеем:
tgβ1=tg(π−β)=−tgβ=−1f/(x).
Точка (x0,f(x0))∈ нормали, уравнение примет вид:
y−f(x0)=−1f/(x0)(x−x0).
6) Логарифмическая производная
Логарифмическая производная– производная от натурального логарифма модуля (абсолютной величины) – данной функции: 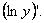
Используя формулу производной сложной функции, найдем, что
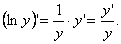 (*)
(*)
Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции.
ТЕОРЕМЫ МАТИХ ЕТИ!
1)Вывести уравнение касательной и нормали к кривой: уравнение касательной можно привести к виду y=kx+b . Вспомним, что угловой коэффициент прямой kравен тангенсу угла наклона прямой к положительному направлению оси Ох или значению производной функции в точке проведения касательной , т.е. y=f `(хо )· x+b.
Для вычисления воспользуемся тем, что касательная проходит через точку А(xo ; f(xo )), т.е. f(xo )=f ´(xo )·x +b,т.е. b = f(xo ) – f ´(xo )·x ,т.е.
y=f `(хо )· x+ f(xo ) – f ´(xo )·x, после преобразований имеем:
y = f(xo) + f ´(xo ) · (x – xo )
нормаль смотреть в определениях
2) Рассмотрим следующие вопросы, который касаются функций.
Если функция непрерывна, то она дифференцируема?
Если функция дифференцируема, то она непрерывна?
Ответ на первый вопрос: из непрерывности функции не следует ее дифференцируемость.
Ответ на второй вопрос: из дифференцируемости функции следует ее непрерывность.
Рассмотрим более конкретно каждый вопрос. Чтобы ответить на данные вопросы необходимо доказать озвученый факт или привести пример, который опровергает этот факт.
Найдем производную следующей функции 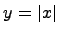 . Хорошо известно, данная функция является непрерывной и, что ее производная будет следующей:
. Хорошо известно, данная функция является непрерывной и, что ее производная будет следующей:
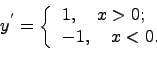
Покажем, что в точке нуль производная не существут. Для этого найдем производную в нуле по определению производной:
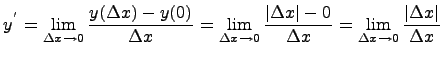
данный предел равен 1, если 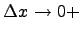 и равен (-1), если
и равен (-1), если 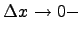 , получаем, что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема.
, получаем, что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема.
Если y = c, где c = const, то y' = 0.
Доказательство
Функция y = c принимает значение, равное c для любого аргумента x. Таким образом, Δy = 0при любомx. Следовательно,
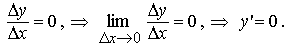
Теорема доказана.
Теорема
3. Пусть функции u = u(x), v= v(x) дифференцируемы. Тогда 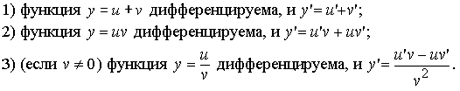
Доказательство
Если аргумент x получит приращение Δx, то функции u, v получат приращения
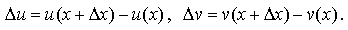
Пусть y = u + v, тогда
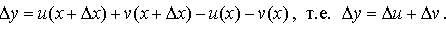
Воспользовавшись свойством предела суммы функции, получаем