Вычислений перемещений методом Мора

Излагаемый ниже метод является универсальным методом определения перемещений (как линейных так и угловых), возникающих в любой стержневой системе от произвольной нагрузки.

Рассмотрим два состояния системы. Пусть в первом из них (грузовое состояние) к балке приложена любая произвольная нагрузка, а во втором (единичное состояние) – сосредоточенная сила 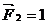(рис.25).

Работа А₂₁ силы 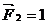на перемещении 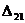, возникающем от сил первого состояния:

.

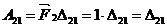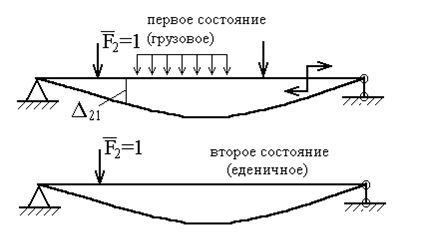
Рис.25

Используя (2.14) и (2.15), выразим А₂₁ (а, значит, и 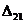) через внутренние силовые факторы:

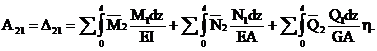(2.17)

Знак “+”, полученный при определении 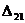, означает, что направление искомого перемещения совпадает с направлением единичной силы. Если определяется линейное смещение, то обобщенная единичная сила представляет собой безразмерную сосредоточенную единичную силу, приложенную в рассматриваемой точке; а если определяется угол поворота сечения, то обобщенная единичная сила – это безразмерный сосредоточенный единичный момент.

Иногда (2.17) записывается в виде:

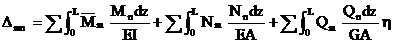(2.18)

где 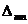- перемещение по направлению силы 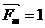, вызванное действием группы сил . Произведения, стоящие в знаменателе формулы (2.18), называются соответственно жесткостями при изгибе, растяжении (сжатии) и сдвиге; при постоянных по длине размерах сечения и одинаковом материале эти величины можно выносить за знак интеграла. Выражения (2.17) и (2.18) называются интегралами (или формулами) Мора.

Наиболее общий вид интеграл Мора имеет в том случае, когда в поперечных сечениях стержней системы возникают все шесть внутренних силовых факторов:

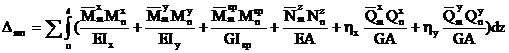(2.19)

Алгоритм вычисления перемещения методом Мора состоит в следующем:

1. Определяют выражения внутренних усилий от заданной нагрузки как функций координаты Z произвольного сечения.

2. По направлению искомого перемещения прикладывается обобщенная единичная сила (сосредоточенная сила – при вычислении линейного перемещения; сосредоточенный момент – при вычислении угла поворота).

3. Определяют выражения внутренних усилий от обобщенной единичной силы как функций координаты Z произвольного сечения.

4. Подставляют выражение внутренних усилий, найденные в п.п.1,3 в (2.18) или (2.19) и интегрированием по участкам в пределах всей длины конструкции определяют искомое перемещение.

Формулы Мора пригодны и для элементов, представляющих собой стержни малой кривизны, с заменой элемента длины dz в подынтегральном выражении элементом дуги ds.

В большинстве случаев плоской задачи используется только один член формулы (2.18). Так, если рассматриваются конструкции, работающие преимущественно на изгиб (балки, рамы, а частично и арки), то в формуле перемещений с соблюдением достаточной точности можно оставить только интеграл, зависящий от изгибающих моментов; при расчете конструкций, элементы которых работают, в основном, на центральное растяжение (сжатие), например, ферм, можно не учитывать деформации изгиба и сдвига, то есть в формуле перемещений останется только член, содержащий продольные силы.

Аналогично, в большинстве случаев пространственной задачи существенно упрощается формула Мора (2.19). Так, когда элементы системы работают преимущественно на изгиб и кручение (например, при расчете плоско-пространственных систем, ломаных стержней и пространственных рам) в (2.19) остаются только первые три члена; а при расчете пространственных ферм – только четвертый член.

Примеры расчетов

Пример 13. Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.26,а), методом Мора.

Рассмотрим три состояния балки: первое (грузовое) – при действии заданной распределенной нагрузки q; ему соответствует эпюра моментов 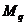(рис.26,б). Второе состояние (единичное) – при действии сосредоточенной силы 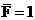, приложенной в точке С; ему соответствует эпюра моментов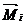

(рис.26,в). Третье состояние (также единичное) – при действии сосредоточенного момента 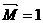, приложенного в точке В; ему соответствует эпюра моментов 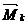(рис.26,г). Примем начало координат на левой опоре; тогда ординаты указанных эпюр в сечении с координатой z соответственно равны:

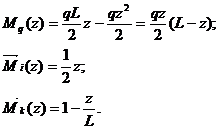
Вычисляем прогиб балки в точке С:

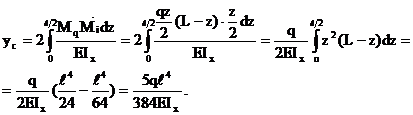
Знак "+" означает, что точка С переместится в направлении действия силы.

Вычисляем угол поворота сечения В:

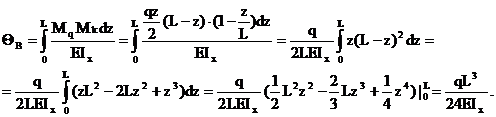
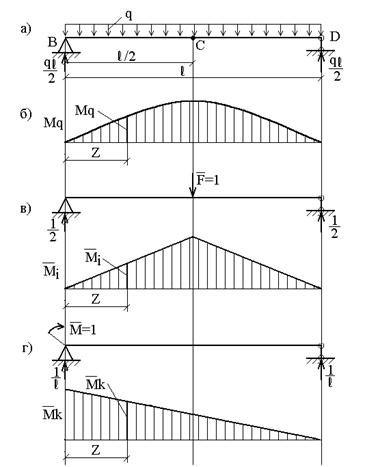
Рис. 26

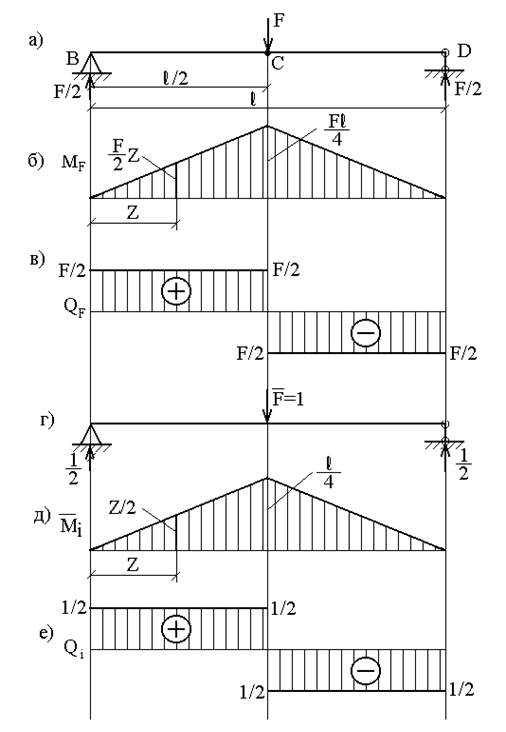
Рис. 27

Знак "+" означает, что сечение В поворачивается в направлении действия момента 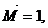то есть по часовой стрелке.

Пример 14. Определить прогиб балки в середине пролета (рис.27,а) методом Мора. Оценить влияние поперечной силы на общую величину прогиба.

Рассмотрим два состояния балки. Первое состояние (грузовое) – при действии силы F (рис.27,а); ему соответствует эпюры изгибающих моментов 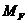(рис.27,б) и поперечных сил 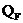(рис.27,в).

Второе состояние (единичное) – при действии силы 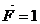(рис.27,г); ему соответствуют эпюры изгибающих моментов 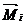(рис.27,д) и поперечных сил 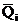(рис.27,е).

В связи с отсутствием продольных сил в поперечных сечениях балки интеграл Мора (2.18) принимает вид:

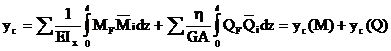
Подставляя значения изгибающих моментов и поперечных сил в сечении с координатой z (рис.27) для составляющих полного перемещения получим:

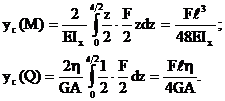
Оценим влияние поперечной силы на общую величину прогиба. Пусть рассматриваемая балка имеет прямоугольное поперечное сечение со сторонами b и h, при этом h=0,1ℓ.

Тогда площадь сечения и его осевой момент инерции равны:

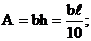
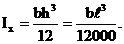
Будем считать, что 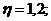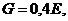тогда:

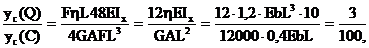
то есть прогиб, обусловленный деформацией сдвига, составляет 3% от прогиба, обусловленного изгибом. Легко убедиться, что при увеличении отношения 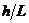влияние поперечных сил на величину прогиба становится еще менее значительным.

Правило Верещагина

Недостатком метода Мора является необходимость получать значения внутренних силовых факторов, входящих в подинтегральные выражения формул (2.18) и (2.19), в общем виде, как функций от z, что становится достаточно трудоемким уже при двух – трех участках разбиения в балках и особенно – в рамах.

Оказывается, что от этого недостатка можно уйти, если непосредственное интегрирование в формулах Мора заменить так называемым перемножением эпюр. Такая замена возможна в тех случаях, когда хотя бы одна из перемножаемых эпюр является прямолинейной. Этому условию соответствуют все системы, состоящие из прямолинейных стержней. Действительно, в таких системах эпюра, построенная от обобщенной единичной силы, всегда будет прямолинейной.

Способ вычисления интеграла Мора путем замены непосредственного интегрирования перемножением соответствующих эпюр называется способом (или правилом) Верещагина и заключается в следующем: чтобы перемножить две эпюры, из которых хотя бы одна является прямолинейной, нужно площадь одной эпюры (если есть криволинейная эпюра, то обязательно ее площадь) умножить на ординату другой эпюры, расположенную под центром тяжести первой.

Докажем справедливость этого правила. Рассмотрим две эпюры (рис.28). Пусть одна из них (M_n) является грузовой и имеет криволинейное очертание, а вторая 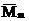соответствует единичной нагрузке и является линейной.

Из рис.28 следует, что 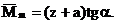Подставим значения 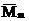в выражение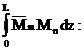

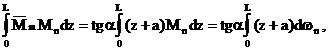
где 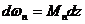- дифференциал площади 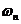эпюры M_n.

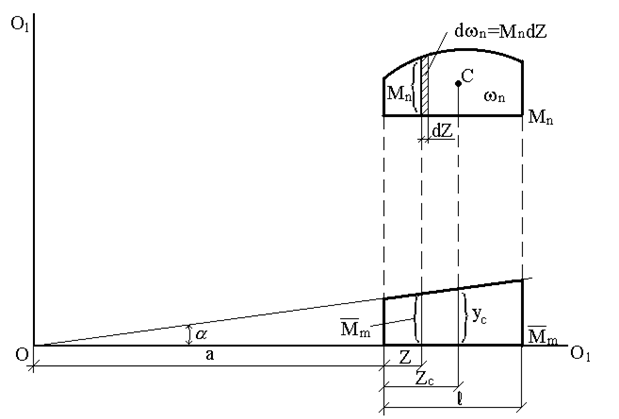
Рис. 28

Интеграл 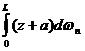представляет собой статический момент площади 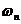относительно оси О – О₁, при этом:

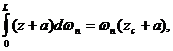
где z_c – абсцисса центра тяжести площади 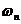, тогда:

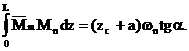
Учитывая, что 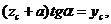получим:

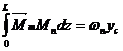(2.20)

Выражение (2.20) определяет результат перемножения двух эпюр, а не перемещения. Чтобы получить перемещение, этот результат нужно разделить на жесткость, соответствующую внутренним силовым факторам, стоящим под знаком интеграла.

2.8 Основные варианты перемножения эпюр

Очевидно, что разнообразие приложенных нагрузок и геометрических схем конструкций приводит к различным, с точки зрения геометрии, перемножаемым эпюрам. Для реализации правила Верещагина нужно знать площади геометрических фигур и координаты их центров тяжести. На рис.29 представлены некоторые основные варианты, возникающие в практических расчетах.

Для перемножения эпюр сложной формы их необходимо разбивать на простейшие. Например, для перемножения двух эпюр, имеющих вид трапеции, нужно одну из них разбить на треугольник и прямоугольник, умножить площадь каждого из них на ординату второй эпюры, расположенную под соответствующим центром тяжести, и результаты сложить. Аналогично поступают и для умножения криволинейной трапеции на любую линейную эпюру.

Если указанные выше действия проделать в общем виде, то получим для таких сложных случаев формулы, удобные для использования в практических расчетах (рис.30). Так, результат перемножения двух трапеций (рис.30,а):

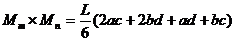(2.21)

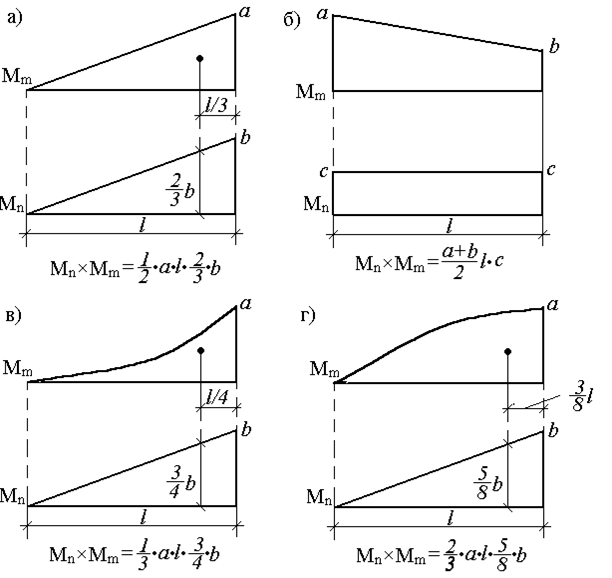
Рис. 29

По формуле (2.21) можно перемножить и эпюры, имеющих вид "перекрученных" трапеций (рис.30,б), но при этом произведение ординат, расположенных по разные стороны от осей эпюр, учитывается со знаком минус.

Если одна из перемножаемых эпюр очерчена по квадратной параболе (что соответствует нагружению равномерно распределенной нагрузкой), то для перемножения со второй (обязательно линейной) эпюрой ее рассматривают как сумму (рис.30,в) или разность (рис.30,г) трапециидальной и параболической эпюр. Результат перемножения в обоих случаях определяется формулой:

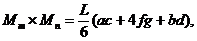(2.22)

но значение f при этом определяется по-разному (рис. 30, в, г).

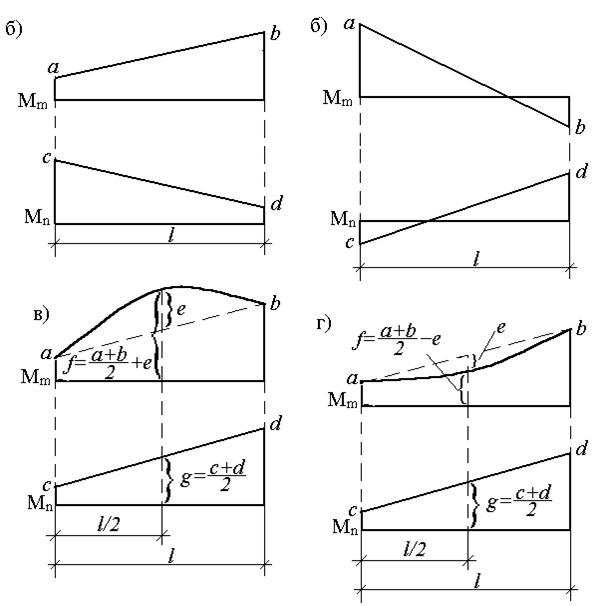
Рис. 30

Возможны случаи, когда ни одна из перемножаемых эпюр не является прямолинейной, но хотя бы одна из них ограничена ломаными прямыми линиями. Для перемножения таких эпюр их предварительно разбивают на участки, в пределах каждого из которых по крайней мере одна эпюра являетя прямолинейной.

Рассмотрим использование правила Верещагина на конкретных примерах.

Пример 15. Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.31,а), способом Верещагина.

Последовательность расчета способом Верещагина – такая же, как и в методе Мора, поэтому рассмотрим три состояния балки: грузовое – при действии распределенной нагрузки q; ему соответствует эпюра M_q (рис.31,б), и два единичных состояния - при действии силы 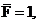приложенной в точке С (эпюра 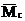, рис.31,в), и момента 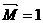, приложенного в точке В (эпюра 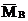, рис.31,г).

Прогиб балки в середине пролета:

.

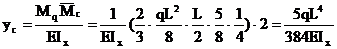Аналогичный результат был получен ранее методом Мора (см. пример 13). Следует обратить внимание на тот факт, что перемножение эпюр выполнялось для половины балки, а затем, в силу симметрии, результат удваивался. Если же площадь всей эпюры M_q умножить на расположенную под ее центром тяжести ординату эпюры 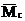( 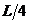на рис.31,в), то величина перемещения будет совершенно иной и неправильной так как эпюра 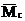ограничена ломаной линией. На недопустимость такого подхода уже указывалось выше.

А при вычислении угла поворота сечения в точке В можно площадь эпюры M_q умножить на расположенную под ее центром тяжести ординату эпюры 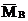( 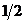, рис.31,г), так как эпюра 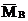ограничена прямой линией:

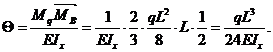
Этот результат также совпадает с результатом, полученным ранее методом Мора (см. пример 13).

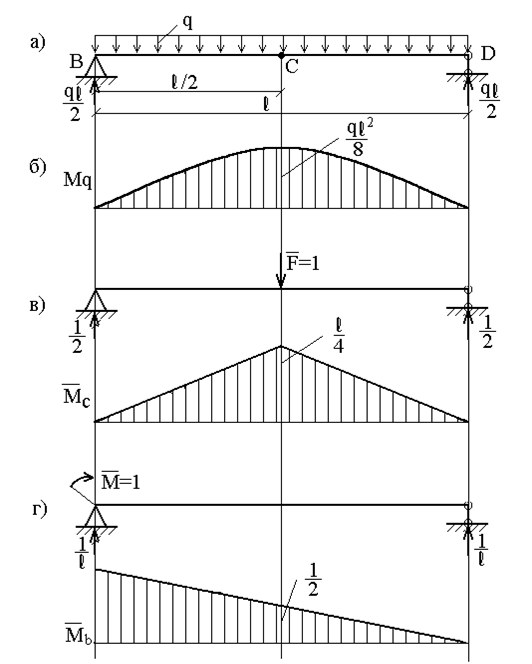
Рис. 31

Пример 16. Определить горизонтальное и вертикальное перемещения точки А в раме (рис.32,а).

Как и в предыдущем примере, для решения задачи необходимо рассмотреть три состояния рамы: грузовое и два единичных. Эпюра моментов M_F, соответствующая первому состоянию, представлена на рис.32,б. Для вычисления горизонтального перемещения прикладываем в точке А по направлению искомого перемещения (т.е. горизонтально) силу , а для вычисления вертикального перемещения силу прикладываем вертикально (рис.32,в,д). Соответствующие эпюры и 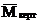показаны на рис.32,г,е.

Горизонтальное перемещение точки А:

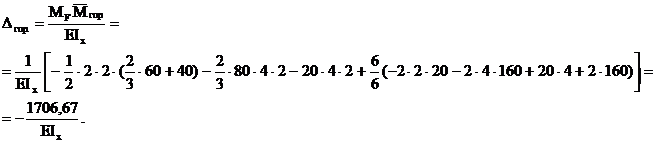
При вычислении 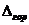на участке АВ трапеция (эпюра M_F) разбита на треугольник и прямоугольник, после чего треугольник с эпюры 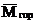"умножен" на каждую из этих фигур. На участке ВС криволинейная трапеция разделена на криволинейный треугольник и прямоугольник, а для перемножения эпюр на участке СД использована формула (2.21).

Знак " - ", полученный при вычислении 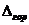, означает, что точка А перемещается по горизонтали не влево (в этом направлении приложена сила 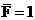), а вправо.

Вертикальное перемещение точки А:

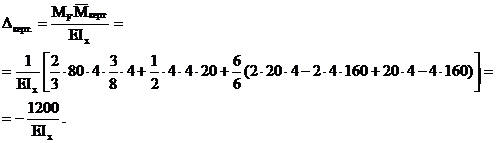
Здесь знак " - " означает, что точка А перемещается вниз, а не вверх.

Отметим, что единичные эпюры моментов, построенные от силы 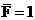, имеют размерность длины, а единичные эпюры моментов построенные от момента 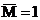, являются безразмерными.

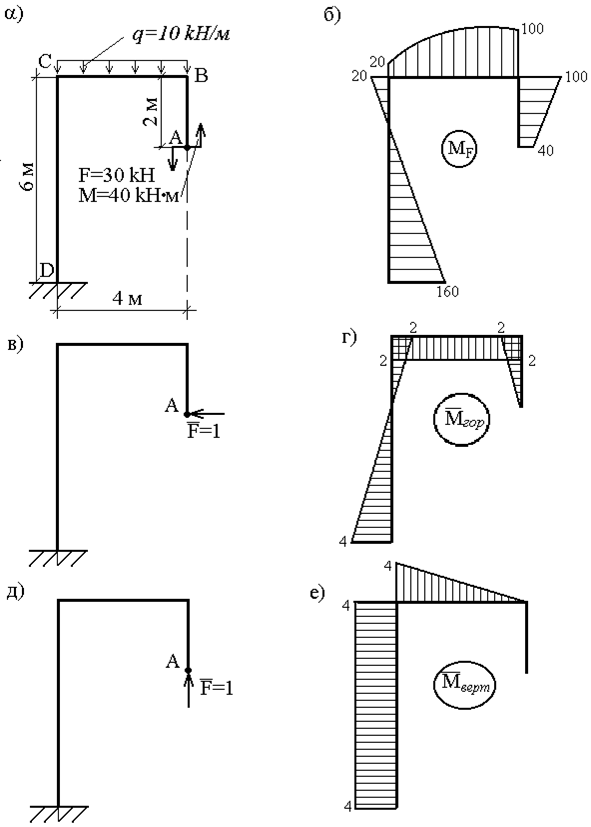
Рис.32

Пример 17. Определить вертикальное перемещение точки А плоско-пространственной системы (рис.33,а).

Рис.23

Как известно (см. гл.1), в поперечных сечениях стержней плоско-пространственной системы возникают три внутренних силовых фактора: поперечная сила Q_y, изгибающий момент M_x и крутящий момент M_кр. Так как влияние поперечной силы на величину перемещения незначительно (см. пример 14, рис.27), то при вычислении перемещения методом Мора и Верещагина из шести слагаемых остаются только два.

Для решения задачи построим эпюры изгибающих моментов M_x,q и крутящих моментов М_кр,q от внешней нагрузки (рис.33,б), а затем в точке А приложим силу 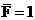по направлению искомого перемещения, т.е. вертикального (рис.33,в), и построим единичные эпюры изгибающих моментов 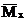и крутящих моментов 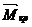(рис.33,г). Стрелками на эпюрах крутящих моментов показаны направления закручивания соответствующих участков плоско-пространственной системы.

Вертикальное перемещение точки А:

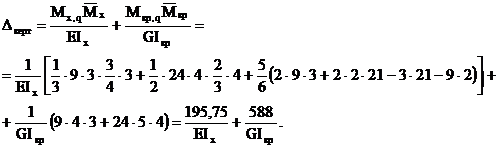
При перемножении эпюр крутящих моментов произведение берется со знаком "+", если стрелки, указывающие направление кручения, сонаправленны, и со знаком " - " – в противном случае.

Глава 3