Дифференциальные уравнения высших порядков. Задача Коши. Понятие о краевых задачах для дифференциальных уравнений. Уравнения, допускающие понижение порядка.
Рассмотрим дифференциальное уравнение п-го порядка:
F (x, y, y′,…, y(n)) = 0, (18.1)
где F предполагается непрерывной функцией всех своих аргументов. Тогда по теореме о существовании неявной функции (см. лекцию ) можно разрешить это уравнение относительно старшей производной:
у(п) = f (x, y, y′,…, y(n-1)) (18.2)
и сформулируем для него (без доказательства) теорему существования и единственности решения:
Теорема 18.1. Существует единственное решение уравнения (18.2), удовлетворяющее условиям
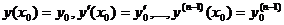 ,(18.3)
,(18.3)
если в окрестности начальных значений (х0 , у0 , у′0,…,у0(п-1)) функция f является непрерывной функцией всех своих аргументов и удовлетворяет условию Липшица по всем аргументам, начиная со второго.
Замечание 1. Так же, как и для дифференциального уравнения 1-го порядка, задача отыскания решения уравнения (18.2), удовлетворяющего условиям (18.3), называется задачей Коши.
Замечание 2. Теорема 18.1 утверждает существование частного решения уравнения (18.2), удовлетворяющего данным начальным условиям. С геометрической точки зрения это соответствует существованию интегральной кривой, проходящей через точку 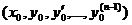 . Но, используя эту теорему, можно доказать и существование общего решения уравнения (18.2), содержащего п произвольных постоянных и имеющего вид:
. Но, используя эту теорему, можно доказать и существование общего решения уравнения (18.2), содержащего п произвольных постоянных и имеющего вид:
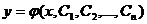 (18.4)
(18.4)
или, в неявной форме:
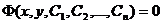 . (18.5)
. (18.5)
Соотношение (18.5) будем называть общим интегралом уравнения (18.1) или (18.2).
Уравнения, допускающие понижение порядка.
В некоторых случаях порядок дифференциального уравнения может быть понижен, что обычно облегчает его интегрирование. Рассмотрим несколько типов подобных уравнений.
1. Уравнение не содержит искомой функции и ее производных по порядок (k – 1) включительно:
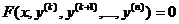 . (18.6)
. (18.6)
В этом случае можно сделать замену р = у(k), которая позволяет понизить порядок уравнения до n – k, так как после замены уравнение примет вид
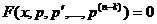 .
.
Из этого уравнения можно найти р = р (х, С1 , С2 ,…, Сn-k), а затем найти у с помощью интегрирования k раз функции р = р (х, С1 , С2 ,…, Сn-k).
Пример.
Уравнение 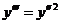 при замене
при замене 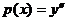 становится уравнением 1-го порядка относительно р:
становится уравнением 1-го порядка относительно р: 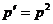 , откуда
, откуда 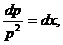
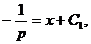
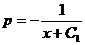 . Тогда
. Тогда
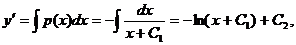
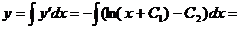
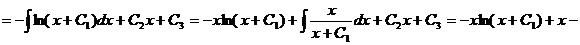
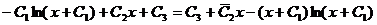 .
.
2. Уравнение не содержит независимой переменной:
F ( y, y′,…, y(n)) = 0. (18.7)
Порядок такого уравнения можно понизить на единицу заменой у′ = р(у). При этом производные функции f(x) по аргументу х нужно выразить через производные р по у:
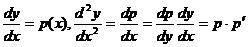 и т.д.
и т.д.
Пример.
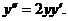 Пусть
Пусть 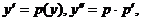 тогда
тогда 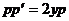 . Отметим частное решение р = 0, то есть
. Отметим частное решение р = 0, то есть 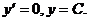 Если
Если 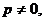 после сокращения на р получим
после сокращения на р получим 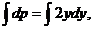
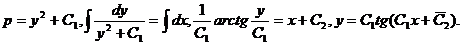
3. Уравнение F (х, y, y′,…, y(n)) = 0 однородно относительно аргументов y, y′,…, y(n), то есть справедливо тождество
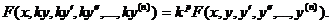
В этом случае можно понизить порядок уравнения на единицу, вводя новую неизвестную функцию z, для которой 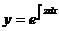 . Тогда
. Тогда 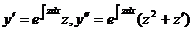 и т.д.
и т.д.
Лекция 19.
Линеаризация диффе6ренциальных уравнений. Линейные дифференциальные уравнения высших порядков. Однородные уравнения, свойства их решений. Свойства решений неоднородных уравнений.
Определение 19.1. Линейным дифференциальным уравнением п-го порядканазывается уравнение, линейное относительно неизвестной функции и ее производных:
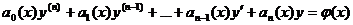 . (19.1)
. (19.1)
Если 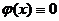 , уравнение называется линейным однородным.
, уравнение называется линейным однородным.
Если а0(х) не равно нулю ни в одной точке некоторого отрезка [a,b], линейное однородное уравнение удобно записывать в форме
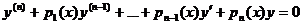 (19.2)
(19.2)
или 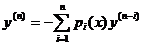 . (19.2′)
. (19.2′)
Замечание 1. Если коэффициенты pi(x) непрерывны на [a,b], то в окрестности любых начальных значений при 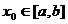 удовлетворяются условия теоремы суще6ствования и единственности.
удовлетворяются условия теоремы суще6ствования и единственности.
Замечание 2. Линейность и однородность уравнения сохраняются при любом преобразовании 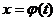 , где
, где 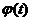 - п раз дифференцируемая функция и
- п раз дифференцируемая функция и 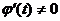 на [a,b], так как
на [a,b], так как 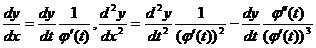 и т.д., то есть производная любого порядка по х является линейной однородной функцией производных по t.
и т.д., то есть производная любого порядка по х является линейной однородной функцией производных по t.
Замечание 3. Линейность и однородность уравнения сохраняются также при линейном однородном преобразовании неизвестной функции y(x) = α(x)z(x).
Определение 19.2. Назовем линейным дифференциальным оператором
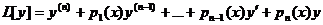 (19.3)
(19.3)
результат применения к функции у операций, задаваемых левой частью уравнения (19.2).
При этом уравнение (19.2) можно записать в виде L[y] = 0.
Свойства линейного дифференциального оператора.
1) Постоянный множитель выносится за знак линейного оператора: L[cy] = cL[y], так как (су)(i) = cy(i).
2) L[y1 + y2] = L[y1] + L[y2].
Действительно, (у1 + у2)(i) = y1(i) + y2(i), откуда следует справедливость сформулированного свойства.
Следствие.
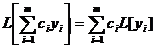 . (19.4)
. (19.4)
Используя свойства линейного оператора, можно указать некоторые свойства решений линейного однородного уравнения (19.2).
Теорема 19.1. Если у1 – решение уравнения (19.2), то и су1, где с – произвольная постоянная, – тоже решение этого уравнения.
Доказательство. Если L[y1] = 0, то по свойству 1) линейного оператора L[сy1] = 0, что и требовалось доказать.
Теорема 19.2. Сумма у1 + у2 решений уравнения (19.2) тоже является решением этого уравнения.
Доказательство. Так как L[y1] = 0 и L[y2] = 0, по свойству 2) линейного оператора L[y1 + у2] = L[y1] + L[y2] = 0, что доказывает утверждение теоремы.
Следствие теорем 19.1 и 19.2. Линейная комбинация 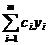 решений уравнения (19.2) у1, у2,…,ут с произвольными постоянными коэффициентами тоже является решением этого уравнения.
решений уравнения (19.2) у1, у2,…,ут с произвольными постоянными коэффициентами тоже является решением этого уравнения.
Если рассматривается линейное неоднородное уравнение (19.1), которое при 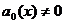 можно записать в виде
можно записать в виде
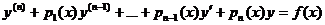 (19.5)
(19.5)
или L[y] = f(x), то при непрерывности функций pi(x) и f(x) оно имеет единственное решение, удовлетворяющее заданным начальным условиям (18.3).
Из свойств линейного оператора следуют свойства решений неоднородного линейного уравнения:
1) Сумма 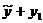 решения
решения 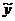 неоднородного уравнения (19.5) и решения у1 соответствующего однородного уравнения (19.2) является решением неоднородного уравнения (19.5). Доказательство.
неоднородного уравнения (19.5) и решения у1 соответствующего однородного уравнения (19.2) является решением неоднородного уравнения (19.5). Доказательство. 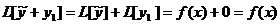 .
.
2) Если yi – решение уравнения L[y] = fi(x), то 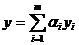 является решением уравнения
является решением уравнения 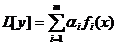 , где αi – постоянные (принцип суперпозицииили наложения). Доказательство.
, где αi – постоянные (принцип суперпозицииили наложения). Доказательство.
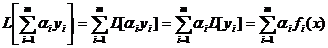 , что и требовалось доказать.
, что и требовалось доказать.
Лекция 20.
Линейная зависимость и независимость системы функций. Определитель Вронского, его свойства. Фундаментальная система решений однородного линейного дифференциального уравнения. Общее решение однородного уравнения.
Определение 20.1. Функции у1(х), у2(х),…, уп(х) называются линейно зависимыми на некотором отрезке [a,b], если существуют такие числа α1, α2,…, αп, хотя бы одно из которых не равно нулю, что
α1у1 + α2у2 + … + αпуп = 0 (20.1)
на рассматриваемом отрезке. Если же равенство (20.1) справедливо только при всех αi=0, функции у1(х), у2(х),…, уп(х) называются линейно независимымина отрезке [a,b].
Примеры.
- Функции 1, x, x², …, xn линейно независимы на любом отрезке, так как равенство α1 + α2x + α3x² + … + αn+1xn = 0 справедливо только при всех αi = 0. Иначе в левой части равенства стоял бы многочлен степени не выше п, который может обращаться в нуль не более, чем в п точках рассматриваемого отрезка.
- Линейно независимой на любом отрезке является система функций
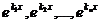 . Если предположить, что эта система линейно зависима, то существуют такие числа α1, α2,…, αп (пусть для определенности
. Если предположить, что эта система линейно зависима, то существуют такие числа α1, α2,…, αп (пусть для определенности 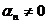 ), что
), что 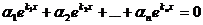 . Разделим полученное равенство на
. Разделим полученное равенство на 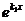 и продифференцируем:
и продифференцируем: 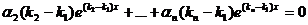 . Проделав эту операцию п-1 раз, придем к равенству
. Проделав эту операцию п-1 раз, придем к равенству 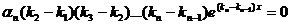 , что невозможно, так как по предположению
, что невозможно, так как по предположению 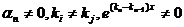 .
. - Подобным образом можно доказать линейную независимость системы функций
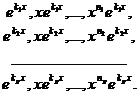
Определение 20.2. Определитель вида
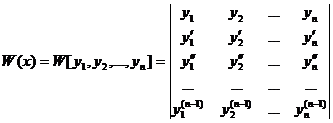 (20.2)
(20.2)
называется определителем Вронскогосистемы функций у1, у2,…, уп.
Теорема 20.1. Если функции у1, у2,…, уп линейно зависимы на отрезке [a,b], то их определитель Вронского на этом отрезке тождественно равен нулю.
Доказательство.
Дифференцируя п-1 раз тождество α1у1 + α2у2 + … + αпуп = 0 , где не все αi = 0, получим линейную однородную систему относительно α1, α2,…, αп:
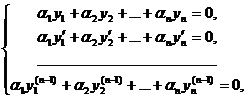 которая по условию должна иметь нетривиальное решение при любом х из отрезка [a,b], а это возможно только в том случае, если главный определитель этой системы (см. правило Крамера) равен нулю. Поскольку этот главный определитель является определителем Вронского для выбранной системы функций, теорема доказана.
которая по условию должна иметь нетривиальное решение при любом х из отрезка [a,b], а это возможно только в том случае, если главный определитель этой системы (см. правило Крамера) равен нулю. Поскольку этот главный определитель является определителем Вронского для выбранной системы функций, теорема доказана.
Теорема 20.2. Если линейно независимые функции у1, у2,…, уп являются решениями линейного однородного уравнения (19.2) с непрерывными на отрезке [a,b] коэффициентами, то определитель Вронского для этих функций не может обратиться в нуль ни в одной точке отрезка [a,b].
Доказательство.
Пусть 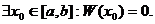 Выберем числа
Выберем числа  , не все равные нулю, так, чтобы удовлетворялась система уравнений
, не все равные нулю, так, чтобы удовлетворялась система уравнений
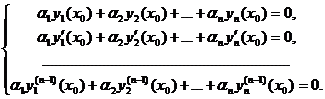 (20.3)
(20.3)
(Определитель этой системы, неизвестными в которой считаем 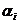 , равен W(x0) и, следовательно, равен нулю, поэтому система имеет ненулевое решение). Тогда по условию теоремы
, равен W(x0) и, следовательно, равен нулю, поэтому система имеет ненулевое решение). Тогда по условию теоремы 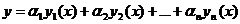 - решение уравнения (19.2) с нулевыми начальными условиями
- решение уравнения (19.2) с нулевыми начальными условиями 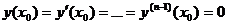 , что следует из системы (20.3). Очевидно, что этим условиям удовлетворяет нулевое решение:
, что следует из системы (20.3). Очевидно, что этим условиям удовлетворяет нулевое решение:
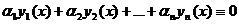 , (20.4) а по теореме существования и единственности это решение единственно. Но при этом из равенства (20.4) следует, что функции у1, у2,…, уп линейно зависимы, что противоречит условиям теоремы. Следовательно,
, (20.4) а по теореме существования и единственности это решение единственно. Но при этом из равенства (20.4) следует, что функции у1, у2,…, уп линейно зависимы, что противоречит условиям теоремы. Следовательно, 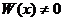 ни в одной точке отрезка [a,b].
ни в одной точке отрезка [a,b].
Замечание. В теореме 20.2 важно, что функции у1, у2,…, уп – решения уравнения (19.2). Для произвольной системы функций утверждение теоремы не справедливо.
Теорема 20.3. Общим решением на [a,b] уравнения (19.2) с непрерывными коэффициентами pi является линейная комбинация 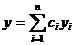 (20.5) п линейно независимых на [a,b] частных решений yi с произвольными постоянными коэффициентами.
(20.5) п линейно независимых на [a,b] частных решений yi с произвольными постоянными коэффициентами.
Доказательство. Для доказательства теоремы с учетом теоремы существования и единственности достаточно показать, что можно подобрать постоянные ci так, чтобы удовлетворялись произвольно заданные начальные условия:
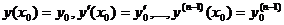 , (20.6) где х0 – произвольная точка отрезка [a,b].
, (20.6) где х0 – произвольная точка отрезка [a,b].
Подставив в равенства (20.6) выражение для у вида (20.5), получим линейную систему из п уравнений относительно неизвестных с1, с2,…, сп:
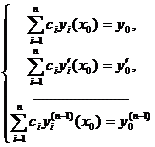 ,
,
определителем которой является определитель Вронского для выбранных п линейно независимых решений рассматриваемого уравнения, который по теореме 20.2 не равен нулю. Следовательно, по правилу Крамера система имеет решение при любых правых частях. Теорема доказана.
Следствие. Максимальное число линейно независимых решений однородного уравнения (19.2) равно его порядку.
Определение 20.3. Любые п линейно независимых решений однородного линейного уравнения (19.2) называются его фундаментальной системой решений.
Таким образом, общее решение уравнения (19.2) является линейной комбинацией любой его фундаментальной системы решений.
Лекция 21.
Однородные линейные дифференциальные уравнения с постоянными коэффициентами. Построение фундаментальной системы решений. Неоднородные линейные дифференциальные уравнения. Частное и общее решения.
Определим вид частных решений однородного линейного уравнения
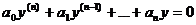 , (21.1)
, (21.1)
в котором коэффициенты ai постоянны. Можно показать, что они имеют вид 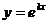 , где k – постоянная. Действительно, при этом
, где k – постоянная. Действительно, при этом 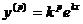 , и после подстановки в уравнение (21.1) получаем:
, и после подстановки в уравнение (21.1) получаем:
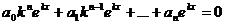 ,
,
или, после сокращения на ekx,
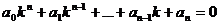 - (21.2)
- (21.2)
так называемое характеристическое уравнение для уравнения (21.1). Числа k, являющиеся его решениями, при подстановке в функцию 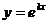 дают частные решения уравнения (21.1). Исследуем различные возможности количества и вида решений характеристического уравнения.
дают частные решения уравнения (21.1). Исследуем различные возможности количества и вида решений характеристического уравнения.
- Все корни уравнения (21.2) действительны и различны: k1, k2,…, kn . Тогда они задают максимально возможное количество линейно независимых решений уравнения (21.1) (их линейная независимость показана в примере 2 лекции 20), то есть определяют фундаментальную систему решений. Следовательно, в этом случае общее решение уравнения (21.1) может быть записано в виде:
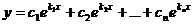 . Пример. Общее решение уравнения
. Пример. Общее решение уравнения 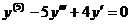 можно найти, решив характеристическое уравнение
можно найти, решив характеристическое уравнение 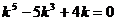 . Разложим левую часть на множители:
. Разложим левую часть на множители: 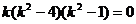 . Следовательно, корни характеристического уравнения:
. Следовательно, корни характеристического уравнения: 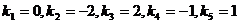 . Поэтому общее решение исходного уравнения имеет вид:
. Поэтому общее решение исходного уравнения имеет вид: 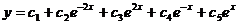 .
. - Корни уравнения (21.2) различны, среди них есть комплексные. При этом, как было показано ранее, они образуют пары комплексно сопряженных чисел. При этом решения уравнения (21.1), соответствующие паре комплексно сопряженных решений уравнения (21.2)
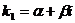 и
и 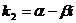 , имеют вид
, имеют вид 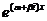 и
и 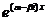 и могут быть заменены двумя действительными решениями: действительной и мнимой частями указанных решений. Следовательно, так как
и могут быть заменены двумя действительными решениями: действительной и мнимой частями указанных решений. Следовательно, так как  , решениями уравнения (21.1) будут
, решениями уравнения (21.1) будут 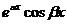 и
и 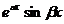 . Пример.
. Пример. 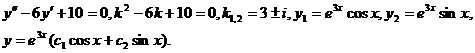

- Характеристическое уравнение имеет кратные корни. В этом случае число линейно независимых решений предыдущих типов меньше п, и для получения фундаментальной системы нужно найти дополнительные решения иного вида. Докажем, что при наличии у характеристического уравнения корня ki кратности αi такими решениями будут
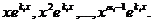 Предположим вначале, что выбранный кратный корень ki = 0. Тогда характеристическое уравнение имеет вид:
Предположим вначале, что выбранный кратный корень ki = 0. Тогда характеристическое уравнение имеет вид:
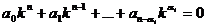 ,
,
а соответствующее дифференциальное уравнение:
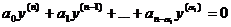 .
.
Очевидно, что частными решениями такого уравнения будут функции 1,x, x²,…, 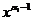 , все производные которых порядка αi и выше равны нулю. Кстати, линейная независимость такой системы функций показана в примере 1 лекции 20.
, все производные которых порядка αi и выше равны нулю. Кстати, линейная независимость такой системы функций показана в примере 1 лекции 20.
Пусть теперь корень характеристического уравнения ki кратности αi не равен нулю. Сделаем замену переменной: 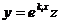 , тогда при подстановке в дифференциальное уравнение его линейность и однородность не нарушается, а коэффициенты изменяются, но по-прежнему остаются постоянными:
, тогда при подстановке в дифференциальное уравнение его линейность и однородность не нарушается, а коэффициенты изменяются, но по-прежнему остаются постоянными:
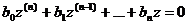 .
.
При этом корни характеристического уравнения
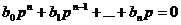 (21.3)
(21.3)
отличаются от корней уравнения
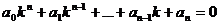
на слагаемое –ki, так как при 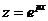
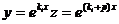 , то есть k = ki + p. Следовательно, уравнение (21.3) имеет корень р = 0 кратности αi , которому соответствуют линейно независимые частные решения
, то есть k = ki + p. Следовательно, уравнение (21.3) имеет корень р = 0 кратности αi , которому соответствуют линейно независимые частные решения 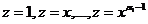 . При обратной замене получаем набор линейно независимых решений исходного уравнения:
. При обратной замене получаем набор линейно независимых решений исходного уравнения: 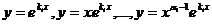 . (21.4)
. (21.4)
Таким образом, каждый кратный корень уравнения (21.2) задает серию линейно независимых частных решений уравнения (21.1), количество которых равно его кратности. Следовательно, вновь построена фундаментальная система решений.
Замечание. Кратные комплексно сопряженные корни задают частные решения вида 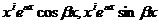 .
.
Примеры.
1. Характеристическое уравнение для уравнения 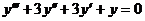 имеет вид (k + 1)³=0, то есть k = -1 – корень кратности 3. Следовательно, фундаментальная система решений состоит из функций
имеет вид (k + 1)³=0, то есть k = -1 – корень кратности 3. Следовательно, фундаментальная система решений состоит из функций 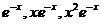 , а общее решение можно записать в виде
, а общее решение можно записать в виде 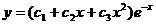 .
.
2. Для уравнения 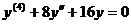 характеристическим уравнением является
характеристическим уравнением является 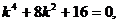 то есть (k²+4)²= 0. Следовательно,
то есть (k²+4)²= 0. Следовательно, 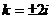 - корни кратности 2. Тогда общим решением исходного дифференциального уравнения является
- корни кратности 2. Тогда общим решением исходного дифференциального уравнения является
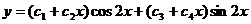 .
.
