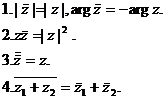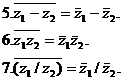Замена переменной в неопределенном интеграле.

Теорема 6.2. Пусть функция f(x) определена на множестве Х, а функция φ(t) – на множестве Φ, причем 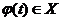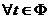. Тогда, если функция f(x) имеет первообразную F(x) на Х, а φ(t) дифференцируема на Φ, то

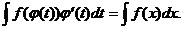(6.1)

Доказательство.

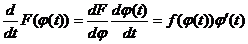, поэтому функция F(φ(t)) является первообразной функции f(φ(t)) φ΄(t). Следовательно, 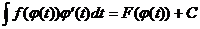. С другой стороны, при x = φ(t) 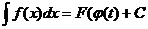. В полученных формулах равны правые части, следовательно, равны и левые, что доказывает справедливость формулы (6.1).

Замечание 1. Формулу (6.1) называют формулой интегрирования подстановкой.

Замечание 2. Часто удобно бывает использовать формулу (6.1) «в обратную сторону»:

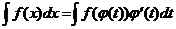, (6.2)

то есть заменять переменную х функцией новой переменной t. Формула (6.2) носит название формулы интегрирования заменой переменной.

Замечание. Формулы (6.1) и (6.2) показывают, что вид первообразной не изменяется при замене независимой переменной х на функцию φ(t), поэтому их называют формулами инвариантности интегрирования.

Примеры.

1. 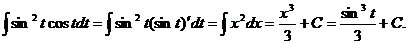При этом была сделана подстановка x = sin t.

2.

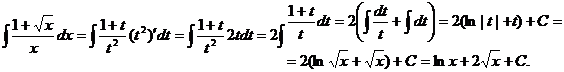
Интеграл был вычислен с помощью замены переменной: x = t².

Формула интегрирования по частям.

Теорема 6.3. Если функции u(x) и v(x) дифференцируемы на некотором промежутке, и на нем существует интеграл 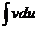, то на нем существует и интеграл 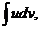причем

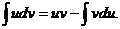(6.3)

Доказательство.

d(uv) = vdu + udv, поэтому udv = d(uv) – vdu. Проинтегрируем обе части полученного равенства, учитывая, что 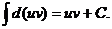Тогда 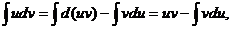что и требовалось доказать. Существование интеграла в левой части равенства следует из существования обоих интегралов в правой части.

Пример.

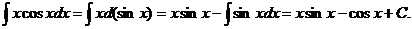
Лекция 7.

Комплексные числа, их изображение на плоскости. Алгебраические операции над комплексными числами. Комплексное сопряжение. Модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы комплексного числа. Корни из комплексных чисел. Показательная функция комплексного аргумента. Формула Эйлера. Показательная форма комплексного числа.

При изучении одного из основных приемов интегрирования: интегрирования рациональных дробей – требуется для проведения строгих доказательств рассматривать многочлены в комплексной области. Поэтому изучим предварительно некоторые свойства комплексных чисел и операций над ними.

Определение 7.1. Комплексным числом z называется упорядоченная пара действительных чисел (а,b) : z = (a,b) (термин «упорядоченная» означает, что в записи комплексного числа важен порядок чисел а и b: (a,b)≠(b,a) ). При этом первое число а называется действительной частью комплексного числа z и обозначается a = Re z, а второе число b называется мнимой частью z: b = Im z.

Определение 7.2. Два комплексных числа z₁ = (a₁ , b₁) и z₂ = (a₂ , b₂ ) равны тогда и только тогда, когда у них равны действительные и мнимые части, то есть a₁ = a₂, b₁ = b₂.

Действия над комплексными числами.

1. Суммой комплексных чисел z₁ = (a₁ , b₁) и z₂ = (a₂ , b₂ ) называется комплексное число z = (a,b) такое, что a = a₁ + a₂ , b = b₁ + b₂ . Свойства сложения: а) z₁ + z₂ = z₂ + z₁; б) z₁ + (z₂ + z₃ ) = (z₁ + z₂ ) + z₃; в) существует комплексное число 0 = (0,0): z + 0 = z для любого комплексного числа z.

2. Произведением комплексных чисел z₁ = (a₁ , b₁) и z₂ = (a₂ , b₂ ) называется комплексное число z = (a,b) такое, что a = a₁a₂ – b₁b₂ , b = a₁b₂ + a₂b₁ . Свойства умножения: а) z₁z₂ = z₂z₁ ; б) z₁ (z₂ z₃) = (z₁ z₂) z₃, в) (z₁ + z₂) z₃ = z₁ z₃ + z₂ z₃ .

Замечание. Подмножеством множества комплексных чисел является множество действительных чисел, определяемых как комплексные числа вида (а,0). Можно убедиться, что при этом определение операций над комплексными числами сохраняет известные правила соответствующих операций над действительными числами. Кроме того, действительное число 1 = (1,0) сохраняет свое свойство при умножении на любое комплексное число: 1∙ z = z.

Определение 7.3. Комплексное число (0, b) называется чисто мнимым . В частности, число (0,1) называют мнимой единицейи обозначают символом i.

Свойства мнимой единицы:

1) i∙i=i² = -1; 2) чисто мнимое число (0,b) можно представить как произведение действительного числа (b,0) и i : (b,0) = b∙i.

Следовательно, любое комплексное число z = (a,b) можно представить в виде: (a,b) = (a,0) + (0,b) = a + ib.

Определение 7.4. Запись вида z = a + ib называют алгебраической формой записи комплексного числа.

Замечание. Алгебраическая запись комплексных чисел позволяет производить операции над ними по обычным правилам алгебры.

Определение 7.5. Комплексное число 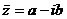называется комплексно сопряженным числу z = a + ib.

3. Вычитание комплексных чисел определяется как операция, обратная сложению: z =(a,b) называется разностью комплексных чисел z₁ = (a₁ , b₁) и z₂ = (a₂ , b₂ ), если a = a₁ – a₂ , b = b₁ – b₂.

4. Деление комплексных чисел определяется как операция, обратная умножению: число z = a + ib называется частным от деления z₁ = a₁ + ib₁ и z₂ = a₂ + ib₂ (z₂ ≠ 0), если z₁ = z∙z₂. Следовательно, действительную и мнимую части частного можно найти из решения системы уравнений: a₂ a – b₂ b = a₁ , b₂ a + a₂ b = b₁.

Геометрическая интерпретация комплексных чисел.

Комплексное число z = (a,b) можно представить в виде точки на плоскости с координатами (a,b) или вектора с началом в начале координат и концом в точке (a,b).

При этом модуль полученного вектора называется модулем комплексного числа, а угол, образованный вектором с положительным направлением оси абсцисс,- аргументом числа. Учитывая, что a = ρ cos φ, b = ρ sin φ, где ρ = | z | - модуль z, а φ = arg z – его аргумент, можно получить еще одну форму записи комплексного числа:

Определение 7.6. Запись вида

z = ρ (cos φ + isin φ) (7.1)

называется тригонометрической формойзаписи комплексного числа.

В свою очередь, модуль и аргумент комплексного числа можно выразить через а и b: 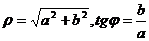. Следовательно, аргумент комплексного числа определен не однозначно, а с точностью до слагаемого, кратного 2π.

Легко убедиться, что операция сложения комплексных чисел соответствует операции сложения векторов. Рассмотрим геометрическую интерпретацию умножения. Пусть 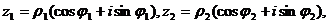тогда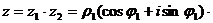

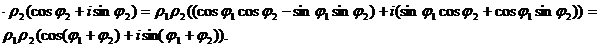
Следовательно, модуль произведения двух комплексных чисел равен произведению их модулей, а аргумент – сумме их аргументов. Соответственно, при делении модуль частного равен отношению модулей делимого и делителя, а аргумент – разности их аргументов.

Частным случаем операции умножения является возведение в степень:

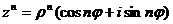(7.2)

- формула Муавра.

Используя полученные соотношения, перечислим основные свойства комплексно сопряженных чисел: