Замена переменной в неопределённом интеграле

Интегрирование подстановкой) и интегрирование по частям.

Интегрирование подстановкой

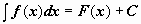Пусть . Тогда 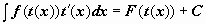. Здесь t(x) - дифференцируемая монотонная функция.

При решении задач замену переменной можно выполнить двумя способами.

1. Если в подынтегральной функции удаётся сразу заметить оба сомножителя, и f(t(x)), и 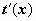, то замена переменной осуществляется подведением множителя 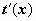под знак дифференциала: 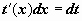, и задача сводится к вычислению интеграла .

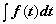Пример 1

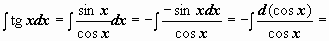(задача сведена к вычислению 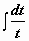, где t = cos x) 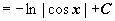(аналогично находится интеграл от 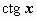); 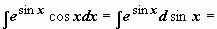(задача сведена к вычислению 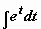, где t = sin x) .

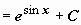2. Замену переменной можно осуществлять формальным сведением подынтегрального выражения к новой переменной. Так, в 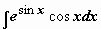имеет смысл перейти к переменной (сделать подстановку) t = sin x.

Выражаем все множители подынтегрального выражения через переменную t:

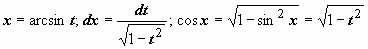; в результате

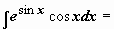
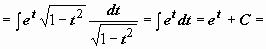(возвращаемся к исходной переменной) .

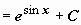Другие примеры:

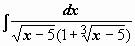. Подынтегральная функция содержит два множителя, ни один из которых не является производной другого, поэтому подводить их под знак дифференциала бесполезно. Попытаемся ввести новую переменную, такую, чтобы корни извлеклись:

= .

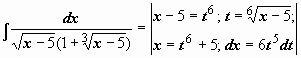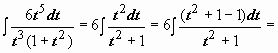
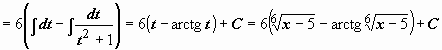Рассмотрим 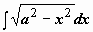(интеграл №19 из табл. неопределённых интегралов). Здесь подынтегральная функция состоит из единственного множителя; можно опять попытаться сделать такую замену переменной, чтобы корень извлёкся. Структура подкоренного выражения подсказывает эту замену: 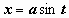(или , ): .

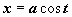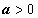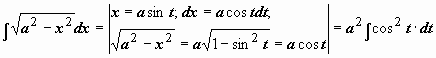Интеграл свёлся к интегралу от квадрата косинуса. При интегрировании чётных степеней синуса и косинуса часто применяются формулы, выражающие 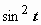и 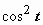через косинус двойного угла:

.

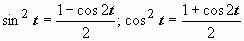Поэтому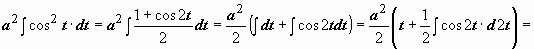

.

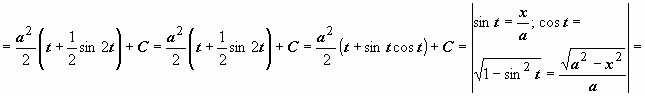
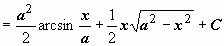Искусство интегрирования в основном заключается в умении видеть необходимые подстановки; оно, как и любое другое искусство, вырабатывается упражнениями. Для основных классов функций требуемые подстановки будут изучаться дальше, здесь мы покажем, с помощью каких преобразований были выведены формулы 17, 15, 20 Таблицы неопределённых интегралов:

.

.

.

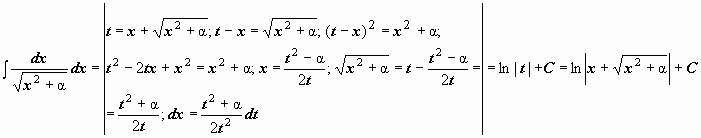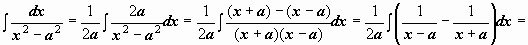
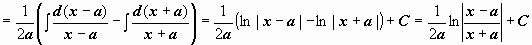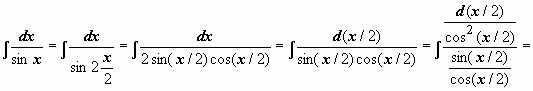
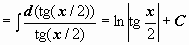Второй интеграл элементарно сводится к первому:

.

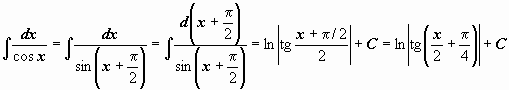Интегрирование по частям

Интегрирование по частям - приём, который применяется почти так же часто, как и замена переменной. Пусть u(x) и v(x) - функции, имеющие непрерывные частные производные. Тогда по формуле дифференцирования произведения d(uv) = u∙dv + v∙du 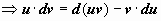. Находим неопределённые интегралы для обеих частей этого равенства (при этом ):

.

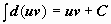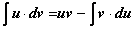Эта формула и называется формулой интегрирования по частям. Часто ее записывают в производных (dv = v’∙dx , du = u’∙dx):

.

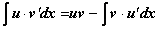Примеры:

. .

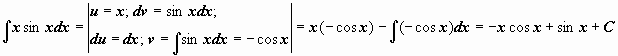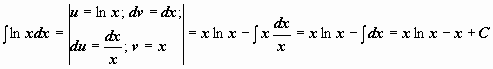Формула интегрирования по частям может применяться неоднократно. При наличии небольшого опыта в простых интегралах нет необходимости выписывать промежуточные выкладки (u = …, dv = …), можно сразу применять формулу, представив интеграл в виде :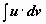

.

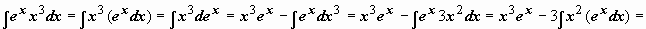
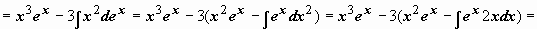
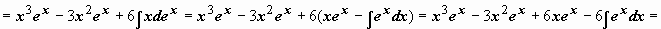
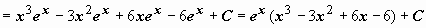Приведённые примеры показывают, для каких функций надо применять (или попытаться применить) формулу интегрирования по частям:

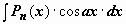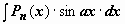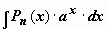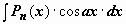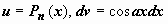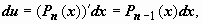
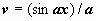1. Интегралы вида , , , где P_n(x) - многочлен n-ой степени. Так, для имеем , , и 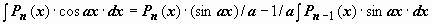. В результате мы получили интеграл того же типа с многочленом степени на единицу меньше. После n-кратного применения формулы степень многочлена уменьшится до нуля, т.е. многочлен превратится в постоянную, и интеграл сведётся к табличному.

2.Интегралы 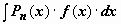, где 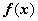- трансцендентная функция, имеющая дробно-рациональную или дробно-иррациональную производную (ln x, arctg x, arcctg x, arcsin x, arcos x). В этом случае имеет смысл взять u = f(x), dv = P_n(x)dx, для того, чтобы в интеграле 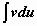участвовала не f(x), а её производная.

Пример:

.

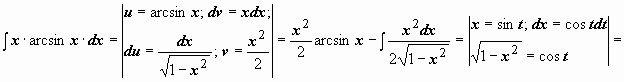
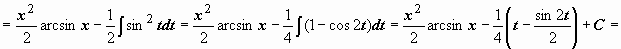
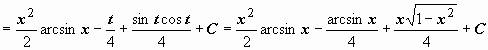3.Для некоторых функций применяется приём “сведения интеграла к самому себе”. С помощью интегрирования по частям (возможно, неоднократного) интеграл выражается через такой же интеграл; в результате получается уравнение относительно этого интеграла, решая которое, находим значение интеграла.

4. Ещё один вид формул, которые обычно получаются с помощью интегрирования по частям, и используются для нахождения интегралов - рекуррентные соотношения. Если подынтегральная функция зависит от некоторого параметра n, и получено соотношение, которое выражает интеграл через аналогичный интеграл с меньшим значением n, то это соотношение и называется рекуррентным соотношением.