Модели поведения фирмы в условиях совершенной и несовершенной конкуренции.

a) В условиях несовершенной конкуренции (монополии) одна или несколько фирм полностью контролируют предложение определенной продукции и цены на неё. С увеличением цены спрос на продукцию падает: P=aq+b, a<0, b>0. Суммарный доход r (выручка) r=pq, где p – цена единицы продукции, q – количество (объем продукции).

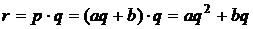, a<0, b>0.

Средний доход на единицу продукции 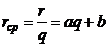. Предельный доход (то есть дополнительный доход от реализации дополнительной продукции) .

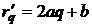Вывод: В условиях монопольного рынка с ростом количества реализованной продукции предельный доход снижается, что приводит к уменьшению (с меньшей скоростью) среднего дохода.

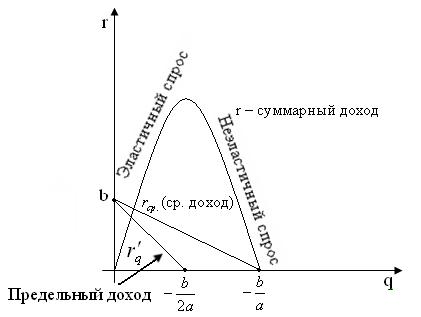
б) В условиях совершенной конкуренции, когда число участников рынка велико, и каждая фирма не способна контролировать уровень цен, устойчивая продажа товаров возможна по преобладающей рыночной цене : p=b. Суммарный доход 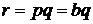, средний доход 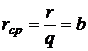, предельный доход .

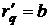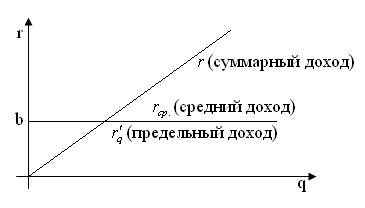Вывод:

В условиях сводного конкурентного рынка средний и предельный доходы совпадают.

Общие модели развития экономики.

1.Факторы экономического роста

2.Модель Харрода – Домара.

3.Модель Солоу.

1. Факторы экономического роста.

Под экономическим ростом (ЭР) обычно понимают увеличение реального дохода в экономике, к которому относят:

· Внутренний национальный продукт,

· ВВП (валовой внутренний продукт),

· НД (национальный доход),

· Рост реального выпуска продукции в расчете на душу населения.

Различают экстенсивный и интенсивный рост экономики.

К экстенсивным факторам относят рост затрат капитала и труда.

К интенсивным факторам – технологический процесс, рост образовательного и профессионального уровня работников, совершенствование управления производством, улучшение законодательства.

В настоящее время широко распространение получили Кейнсианский и монетаристский подходы к прогнозированию и регулированию рыночной экономики.

Кейнс считал, что деньги воздействуют на развитие экономики не через цены, а через норму ссудного процента. Рост нормы ссудного процента удорожает кредит и ведет к сокращению инвестиций в производство, а снижение нормы ссудного процента стимулирует инвестиции в производство.

Монетаристы считают, что скорость обращения денег является переменной величиной и сформулировали “денежное правило” – среднегодовой прирост денежной массы может составлять 4 – 5% в год при среднегодовом увеличении валового национального продукта ≈ на 3% и незначительном снижении скорости оборота денег.

2.Модель Харрода – Домара.

Наиболее простой кейнсианской моделью роста является модель Харрода – Домара.

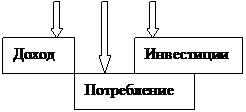
Эта модель описывает динамику дохода Y(t), который является суммой потребления C(t) и инвестиций I(t). Y(t) = C(t) + I(t) (1)

Величина 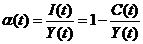называется нормой накопления в момент времени t.

Основной предпосылкой модели роста является формула взаимосвязи между инвестициями и скоростью роста дохода, предполагается, что скорость роста дохода 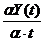пропорциональна инвестициям: 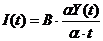, (2).

B – коэффициент капиталоемкости прироста дохода , обратная величина 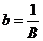- называется коэффициентом капиталоотдачи.

В модели включается ряд предпосылок:

1. Модель не учитывает выбытия капитала

2. Инвестиции мгновенно переходят в прирост капитала: 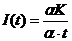(за бесконечно малый промежуток времени 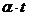инвестиции равны приросту капитала )

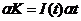3. 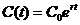- потребление подчинено экспоненциальному закону, r – постоянный темп роста потребления.

4. Модель не учитывает технического процесса.

Подставим (2) в уравнение (1), учитывая 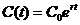, где C₀ – начальное потребление.

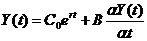или 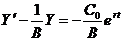- д. у. 1-го порядка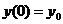

Решив эту задачу Коши, получим .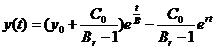

Рассмотрим частные случаи:

1) 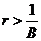, то есть темп роста потребления превышает коэффициент капиталоотдачи. Потребление будет занимать с ростом r все большую часть дохода и в конце концов сведет к нулю сначала инвестиции, а затем и доход.

2) 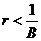, тогда поведение модели зависит от нормы накопления в начальной момент времени .

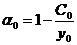3.Модель Солоу.

Модель позволяет более точно описать некоторые особенности макроэкономических процессов.

1.ПФ в этой модели нелинейная.

2.Модель учитывает выбытие основного капитала.

3.Модель включает описание динамики трудовых ресурсов.

Состояние экономики в модели задается пятью переменными, которые являются функциями времени:

Y – ВВП (валовой внутренний продукт)

C – потребление

I – инвестиции

L – число занятых в производстве

K – фонды (капитал)

В модель включаются:

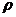- норма накопления, т.е. доля валовых инвестиций в ВВП

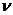- годовой темп прироста числа занятых в производстве.

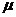- доля выбывшего за год капитала , , .

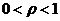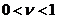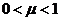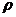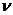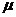, , - постоянны во времени.

Предполагается, что выпуск продукции в каждый момент времени определяется неоклассической ПФ: .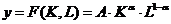

Модель Солоу в абсолютных показателях:

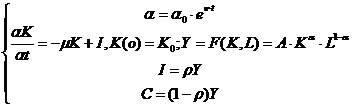
Введем удельные показатели:

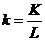- фондовооруженность,

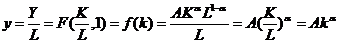
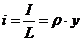- удельные инвестиции на одного занятого,

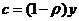- среднедушевое потребление на одного занятого.

Модель Солоу в удельных показателях имеет вид: , , , , , .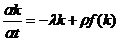

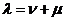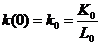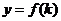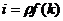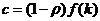Изменяющиеся во времени показатели называются соответственно абсолютными и относительными траекториями.

Рекомендуемая литература.

1. Ильин В.А., Куркина А.В. Высшая математика. Издательство Проспект. Издательство Московского университета, 2005.

2. Кудрявцев Л.Д. Курс математического анализа. М. :"Высшая школа", 1988. Учебник.

3. Пискунов Н.С. Дифференциальное и интегральное исчисления. М. :"Наука", 1976. Учебник.

4. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. М. :"Финансы и статистика", 1992. Учебник.

5. Карасев Ф.И., Аксютина З.М., Савельева В.И. Курс высшей математики для экономических вузов, т.1, 2. М.: "Высшая школа", 1982. Учебное пособие.

6. Под ред. проф. Кремера Н.Ш. Высшая математика для экономистов. М., ЮНИТИ, 2006. Учебник.

7. Шипачев В.С. Высшая математика. М.: Высшая школа, 1998.

8. Лунгу К.Н., Письменный Д.Т., Федин С.Н. Сборник задач по высшей математике. 1 курс. М., АЙРИС ПРЕСС, 2003.

9. Федосеев В.В. Экономико-математические методы и прикладные модели. Учебное пособие для вузов. М., ЮНИТИ, 2002.

10. Малыхин В.И. Математическое моделирование в экономике. Учебно-практическое пособие для вузов. Изд. УРАО, 1998.