Определение производной. Механический, геометрический, экономический смысл производной.

Касательная и нормаль к графику функции.

Дифференцируемость и непрерывность.

1.1.Определение производной. Механический, геометрический, экономический смысл производной.

Пусть функция 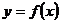определена на множестве 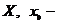внутренняя точка множества X, то есть принадлежит множеству с некоторой своей окрестностью. Аргументу 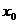дадим приращение 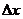, при этом функция получит приращение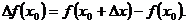

Определение. Производной функции в точке 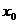называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к 0, то есть

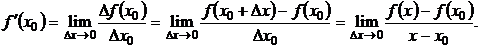
При этом используются обозначения:

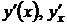– по Лагранжу; 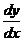– по Лейбницу; 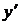– по Ньютону.

Запись 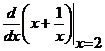следует понимать как производную функции 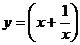в точке .

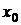Физический смысл производной заключается в том, что

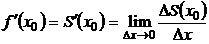– мгновенная скорость прямолинейного движения в момент времени 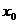. В самых различных задачах (в том числе и экономических) производная функции интерпретируется как скорость изменения величины y относительно величины x.

Геометрический смысл производной: рассмотрим график функции 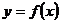, MM₀ – секущая.

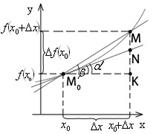Определение. Касательной к графику функции 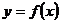в точке M₀ называется предельное положение секущей MM₀, когда точка M движется к точке M₀ по графику функции .

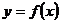Также: 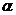– угол наклона касательной к оси оx, 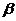– угол наклона секущей к оси оy.

Если .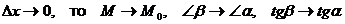

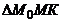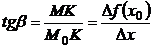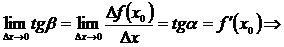
Рассмотрим : ; 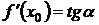– производная функции в точке 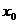есть тангенс угла наклона касательной к графику функции 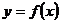в точке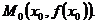

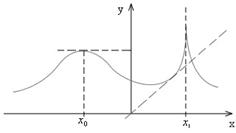Замечание. 1) Если существует конечная производная 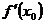, то к графику функции 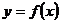в точке 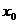можно провести единственную касательную;

2) Если 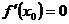, то касательная к графику функции 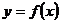в точке 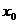параллельна оси оx.

3) В точке 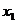касательная не существует и производная функции также не существует.

Касательная и нормаль к графику функции.

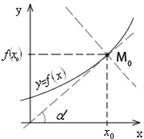Составим уравнение касательной к графику функции 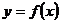в точке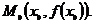

Пользуясь уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом 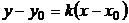и, считая 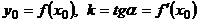получим уравнение касательной в точке M₀: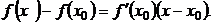

Определение. Нормалью к графику функции 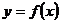называется прямая, которая проходит через точку касания перпендикулярно касательной.

Так как угловые коэффициенты взаимно перпендикулярных прямых связаны

соотношением 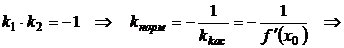уравнение нормали имеет вид: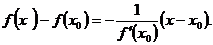

Дифференцируемость и непрерывность.

Если функция 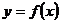имеет конечную производную в точке 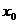, то функция называется дифференцируемой в точке .

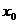Теорема. Если функция 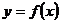дифференцируема в точке 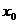, то функция 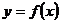непрерывна в точке .

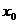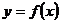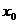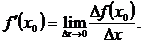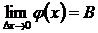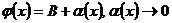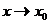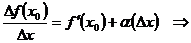
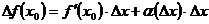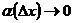Доказательство. Так как функция дифференцируема в точке , то в этой точке она имеет конечную производную Также по свойству пределов если , то при . Тогда , где при .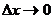

Получили, что 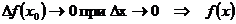непрерывна в точке 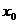по определению непрерывности функции на языке приращений.

Теорема доказана.

Лекция 2. Правила дифференцирования.

Правила дифференцирования суммы, произведения и частного двух функций