Проектировочный расчет вала при кручении

Для участка вала, в котором возникает наибольший крутя­щий момент, определяют диаметр вала для сплошного круглого сечения из условий прочности и жесткости.

1. Определение диаметра вала из условия прочности: t = М_К/W_Р £ [t_к] → W_Р ≥ М_К / [t]

Учитывая, что для круглого се­чения W_p= pd³/16 = 0,2d³, определяется необходимый по прочности диа­метр поперечного сечения вала.

2. Определение диаметра вала из условия жесткости:

φ_о = М_кmax / ( GI_p )≤ [j_о] → I_p= М_к/ G φо]

Учитывая, что для круглого се­чения 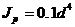, определяется необходимый по жесткости диаметр по­перечного сечения вала.

Из двух полученных диаметров вала выбирают наибольший.

ТЕМА 6. ИЗГИБ

· Изгиб – такой вид деформации, при котором в любом поперечном сечении бруса возникает изгибающий момент М_и.

· Брус, работающий на изгиб – балка. На изгиб работают оси, валы и другие детали конструкций.

· Если все силы лежат в одной плоскости – изгиб называют плоским;

· Если в любом поперечном сечении бруса возникает только изгибающий момент – изгиб называют чистым;

· Изгиб, при котором в поперечном сечении балки возникают изгибающий момент и поперечная сила, называется поперечным.

· Если внешние силы перпендикулярны продольной оси балки, при этом силовая плоскость совпадает с плоскостью симметрии балки, то изгиб – прямой.

· Для определения внутренних силовых факторов пользуются методом сечений.

ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ ПРИ ПРЯМОМ ПОПЕРЕЧНОМ ИЗГИБЕ

· Поперечная сила в сечении балки численно равна алгебраической сумме всех внешних сил, действующих справа или слева от сечения Q = ∑F_{i ост. части}

· Изгибающий момент в сечении балки численно равен алгебраической сумме моментов относительно центра тяжести сечения всех внешних сил, действующих справа или слева от сечения.

ПРАВИЛА ЗНАКОВ ДЛЯ Q и М_и

Q

Для левой части Для правой части

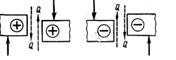
М_и

Для определения опорных реакций пользуются правилами знаков статики; для определения знаков изгибающего момента и поперечной силы — правилами знаков сопротивления материалов.

ПРАВИЛА ПОСТРОЕНИЯ ЭПЮР ПРИ ИЗГИБЕ (СОСРЕДОТОЧЕННАЯ НАГРУЗКА)

1. Для участка, где отсутствует распределенная нагрузка, поперечная сила постоянна, а изгибающий момент меняется по линейному закону, т.е график М_и – наклонная линия.

2. В частном случае, когда поперечная сила на участке равна нулю, изгибающий момент постоянен, график М_и – прямая линия, параллельная оси z.

3. В том месте, где к балке приложена внешняя сосредоточенная сила, на эпюре Q возникает скачок на величину приложенной силы, а на эпюре моментов – излом.

4. В сечении, где к балке приложена пара сил (момент), на эпюре М_и возникает скачок на величину момента. Поперечная сила при этом не изменяется.

5. На конце балки поперечная сила равна приложенной в этом сечении внешней силе.

6. На конце балки М_и равен нулю, за исключением случаев, когда в этом сечении приложен внешний момент. В этом случае М_и равен внешнему моменту.

7.

ПОСТРОЕНИЕ ЭПЮР Q и М

(ПРИЛОЖЕНЫ СОСРЕДОТОЧЕННЫЕ СИЛЫ И РАСПРЕДЕЛЕННЫЕ НАГРУЗКИ)

1. Для участка балки с равномерно распределенной нагрузкой поперечная сила Q изменяется по линейному закону, т.е. эпюра Q – наклонная прямая линия.

2. Изгибающий момент изменяется по квадратичному закону, эпюра М_и –парабола, причем, если распределенная нагрузка направлена вниз, то парабола обращена выпуклостью наверх и наоборот.

3. В сечении, где эпюра пересекает ось , т.е Q = 0, М_и – экстремален.