Глава 27. задачи с несколькими целевыми функциями

Формулировка задачи

В рассматриваемых выше задачах линейного программи­рования математические модели имели одну целевую функцию, для которой находилось максимальное или минимальное зна­чение экономического показателя. Однако на практике часто требуется найти экстремальные значения нескольких эконо­мических показателей. В этом случае математическая модель имеет несколько целевых функций, причем некоторые из них требуют нахождения максимального, а другие — минималь­ного значений. Поэтому ставится задача нахождения такого компромиссного (субоптимального) решения модели, в кото­ром значения всех рассматриваемых экономических показате­лей были бы приближены к экстремальным значениям.

Нахождение компромиссного решения относится к много­критериальным задачам оценки оптимальности.

В настоящее время подобные задачи математически недо­статочно разработаны и для практической деятельности реша­ются следующими способами.

1. Производится ранжирование показателей, т.е. располо­жение их в порядке значимости, важности. Затем при­ступают к поиску решения, оптимального по наиболее важному из них. Задавшись допустимой величиной из­менения первого критерия, ищут решение по второму критерию, наилучшему в полученной области, и т.д. По­рядок значимости и допустимые диапазоны выбирают произвольно.

2. Построение единого (интегрального) показателя эффек­тивности посредством суммирования произведений име­ющихся показателей на "весовые" коэффициенты (коэф­фициенты важности показателей).

3. Превращение всех целевых функций, кроме одной, в ограничения.

Математическая модель нахождения компромиссного решения

Дана математическая модель экономической задачи, в ко­торой две целевые функции и система ограничений линейны. Найдем компромиссное решение по двум показателям, один из которых требует отыскания максимума, а другой — мини­мума:

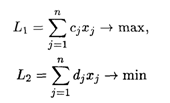
при ограничениях:

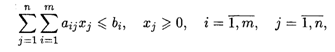
где L₁, L₂ — значения целевых функций (экономические пока­затели), для упрощения записи опущены обозначения аргумен­та; a_ij, c_j, d_j, b_i — коэффициенты; x_j — переменные.

Решим задачу по каждому показателю в отдельности и найдем оптимальные значения L_1max, L_2min.

Проделав преобразования над целевыми функциями, полу­чим математическую модель нахождения компромиссного ре­шения задачи с двумя целевыми функциями:

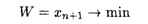
при ограничениях:

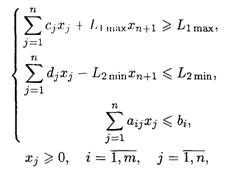
где W — целевая функция; x_n+1 — наибольшее относительное значение экономических показателей.

Математическая модель будет аналогичной в случае на­хождения компромиссных решений задач, имеющих три целе­вые функции и более.

Рассмотрим нахождение компромиссного решения экономи­ческой задачи, математическая модель которой имеет три це­левые функции.