Нахождение оптимальных путей транспортировки грузов при нестабильной загрузке дорог
Имеются три поставщика однородного товара с объемами поставок: а1 = 100 т, а2 = 200 т, a3 = 100 т и четыре потребителя с объемами потребления b1 = - 80 т, b2 = 120 т, b3 = 150 т, b4 = 50 т. Стоимость транспортных расходов изменяется в определенном диапазоне в зависимости от загрузки дороги и задана матрицей
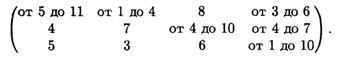
Определить оптимальное решение перевозок, обеспечивающее минимальные транспортные затраты.
Решение. В матрицу расходов введем параметр λ, где 0 ≤ λ ≤ 3. Получим
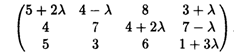
Полагая λ = 0, решаем задачу методом потенциалов, определим оптимальное решение перевозок. Распределительная таблица этого решения будет иметь вид табл. 25.5.
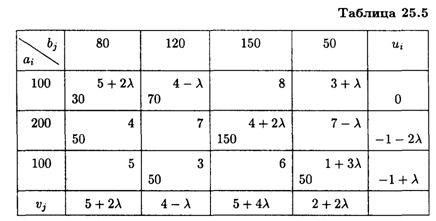
В таблице ui и vj — потенциалы строк и столбцов. Для занятых клеток они определяются из условия
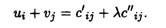
Полагая u1 = 0, v1 + и1 = 5 + 2λ, получаем v1= 5 + 2λ,
v2 + и1 = 4 — λ, откуда v2 = 4 — λ;
v1 + u2 = 4 или 5 + 2λ + u2 = 4, откуда и2 = -1 - 2λ;
v3 + u2 = 4 + 2λ или -1 – 2λ + v3 = 4 + 2λ, v3 = 5 + 4λ.
Аналогично находим, что u3 = -1 + λ, v4 = 2 + 2λ.
Оценки свободных клеток находим по формуле
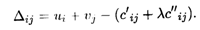
Имеем
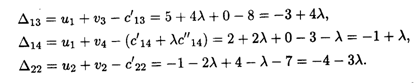
Аналогично находим, что Δ24 = -6 + λ, Δ31 = -1 + 3λ, Δ33 = -2 + 5λ.
Решение, полученное при λ = 0, является оптимальным для всех значений параметра λ, удовлетворяющих условию
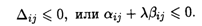
Имеем
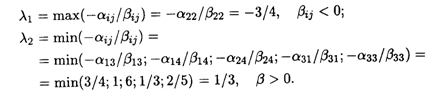
Так как по условию задачи λ ≥ 0, то оптимальное решение сохраняется при 0 ≤ λ ≤ 1/3. При этом минимальная стоимость транспортных расходов составляет
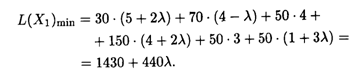
Таким образом, при λ 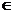 [0; 1/3] L(X1)min = 1430 + 440λ и
[0; 1/3] L(X1)min = 1430 + 440λ и
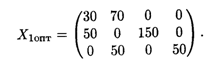
Чтобы получить оптимальное решение при λ ≥ 1/3, перераспределим поставки товаров в клетку (3, 1), где λ2 = 1/3. Вновь полученное распределение представлено в табл. 25.6.
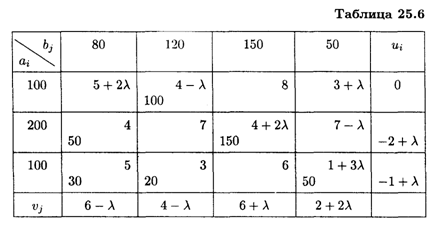
Находим оценки свободных клеток:

Определим пределы изменения λ:
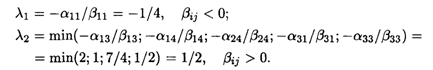
Полученное в таблице оптимальное решение сохраняется при 1/3≤ λ≤ 1/2. При этом L(X2)min = 1460 + 350λ. Итак,

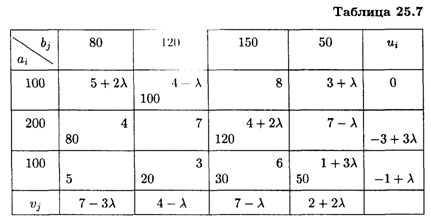
Перераспределим поставки грузов в клетку (3, 3), где λ2 = 1/2. Получим новое распределение (табл. 25.7). Находим оценки свободных клеток:

Определим пределы изменения λ:
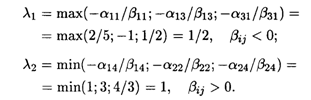
Оптимальное решение сохраняется при 1/2 ≤ λ ≤ 1. При этом L(Х3)min = 1490 + 290λ. Итак,
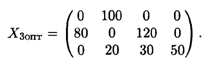
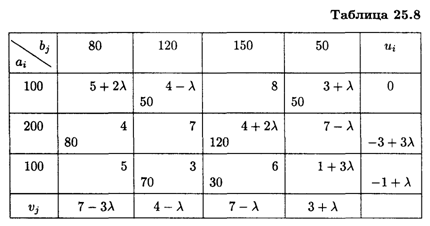
Перераспределим поставки товаров в клетку (1, 4), где λ2 = 1 (табл. 25.8).
Оценки свободных клеток:

Пределы изменения λ:
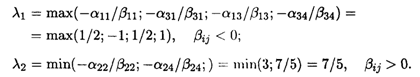
Полученное в предыдущей таблице оптимальное решение сохраняется при λ ≤ 7/5. При этом L(Х4)min = 1540 + 240λ. Итак,
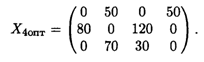
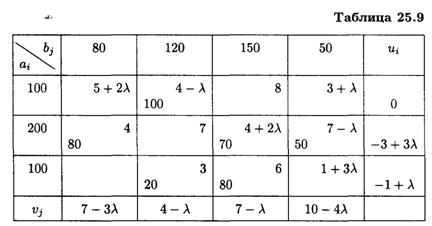
Перераспределим поставки грузов в клетку (2, 4), где λ2 = 7/5 (табл. 25.9).
Оценки свободных клеток:


Пределы изменения λ:

Оптимальное решение сохраняется при 7/5≤ λ≤ 3. При этом L(X5)min = 1890 – 10λ. Итак,
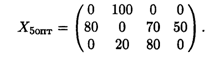
УПРАЖНЕНИЯ
Решить следующие задачи параметрического программирования с параметром в целевой функции.
25.1. L(  ) = -λx1 — х2 → min, 1 ≤ λ ≤ 11 при ограничениях:
) = -λx1 — х2 → min, 1 ≤ λ ≤ 11 при ограничениях:
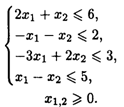
25.2. L(  ) = 5x1 + (2 + 3λ)x2 → max, 0 ≤ λ ≤ 10 при ограничениях:
) = 5x1 + (2 + 3λ)x2 → max, 0 ≤ λ ≤ 10 при ограничениях:
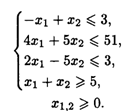
25.3. L(  ) = 2x1 + (3 + 4λ)x2 → max, -
) = 2x1 + (3 + 4λ)x2 → max, -  < λ <
< λ <  при ограничениях:
при ограничениях:
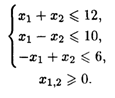
25.4. L(  ) = (1 + λ)x1 + (2 - λ)x2 → min, -1 ≤ λ ≤ 4 при ограничениях:
) = (1 + λ)x1 + (2 - λ)x2 → min, -1 ≤ λ ≤ 4 при ограничениях:
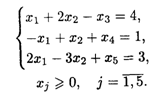
25.5. L(  ) = (3 + 3λ)x1 + 2x2 + (5 – 6λ)x3 → max, -
) = (3 + 3λ)x1 + 2x2 + (5 – 6λ)x3 → max, -  < λ <
< λ <  при ограничениях:
при ограничениях:
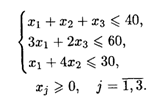
Решить следующие транспортные параметрические задачи.
25.6. Произвести транспортировку однородного груза с трех складов с объемами хранения 100, 200, 200 т соответственно пяти оптовым рынкам с потребностями 80, 70, 100, 150, 100 т соответственно. Стоимость транспортных расходов задана матрицей
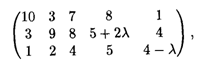
причем стоимость перевозки груза со второго склада на четвертый рынок и с третьего склада на пятый рынок изменяется в некотором диапазоне 0 ≤ λ ≤ 2.
Определить план перевозок, обеспечивающий минимальные транспортные расходы в заданном диапазоне изменения параметра λ.
25.7. Имеются четыре поставщика однородного груза с объемами поставок 100, 70, 70, 20 т и три потребителя с объемами потребления 120, 80, 60 т. Cтоимость транспортных расходов задана матрицей
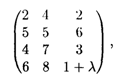
причем стоимость перевозки груза от четвертого поставщика до третьего потребителя изменяется в диапазоне 0 ≤ λ ≤ 9.
Определить оптимальный план перевозок, обеспечивающий минимальные транспортные расходы.
