Прогнозирование эффективного использования производственных площадей

Рассмотрим следующую задачу.

Для улучшения финансового положения фирма приняла ре­шение об увеличении выпуска конкурентоспособной продук­ции, для чего принято решение об установке в одном из це­хов дополнительного оборудования, занимающего 19/3 м² пло­щади. На приобретение дополнительного оборудования фирма выделила 10 усл. ед., при этом она может купить оборудование двух видов. Приобретение 1-го комплекта оборудования 1-го вида стоит 1,0 усл. ед., 2-го вида — 3 усл. ед. Приобретение одного комплекта оборудования 1-го вида позволяет увеличить выпуск продукции в смену на 2 шт., а одного комплекта обору­дования 2-го вида — на 4 шт. Зная, что для установки одного комплекта оборудования 1-го вида требуется 2м² площади, а для оборудования 2-го вида — 1м² площади, определить такой набор дополнительного оборудования, который дает возмож­ность максимально увеличить выпуск продукции.

Решение. Составим математическую модель задачи. Предположим, что фирма приобретает х₁ комплектов допол­нительного оборудования 1-го вида и x₂ комплектов оборудо­вания 2-го вида. Математическая модель задачи будет иметь вид

при ограничениях:

Получим задачу целочисленного программирования, так как неизвестных только два (x₁ и x₂). Найдем решение задачи графическим способом (рис. 24.1).

ОABC — область допустимых решений (ОДР). Оптималь­ное решение задача имеет в точке B (9/5, 41/15), при этом мак­симальное значение целевой функции составляет 218/15 ед. По­лученное оптимальное решение нецелочисленное.

Условию целочисленности переменных удовлетворяют ко­ординаты 12 точек. Чтобы найти точку, координаты которой определяют решение исходной задачи, заменим многоугольник ОABC многоугольником OKEMRNF, содержащим все допус­тимые точки с целочисленными координатами.

Строим вектор 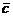(2, 4). Линию уровня перемещаем по на­правлению 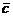, получим в точке Е (1, 3) максимальное значение целевой функции:

Таким образом, фирме следует приобрести один комплект оборудования 1-го вида и три комплекта оборудования 2-го ви­да, что обеспечит ей при имеющихся ограничениях на произ­водственные площади и денежные средства максимальное уве­личение выпуска продукции, равное 14 усл. ед. в смену.

Метод Гомори

Решим эту же задачу методом Гомори, ее математическая модель:

ограничения:

Симплексная таблица представлена в табл. 24.1.

Получим

Найдем дробные части чисел 9/15 и 41/15:

Учитывая дробные части чисел 3/5 и - 1/5:

составляем дополнительное ограничение целочисленности для 1-й строки:

которое вводим в табл. 24.2.

Получим

Сравнивая полученное значение целевой функции целочис­ленного решения со значением при оптимальном решении, за­метим, что условие целочисленности задачи приводит к умень­шению значения целевой функции.

Ответ. 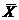_цел. = (1, 3), L( ) = 14.

УПРАЖНЕНИЯ

Найти целочисленное решение следующих задач.

24.1. L( ) = 16x₁ + 9x₂ → max при ограничениях:

24.2. L( ) = 2x₁ + 3x₂ → min при ограничениях:

24.3. L( ) = 3x₁ + x₂ → max при ограничениях:

24.4. L( ) = 4x₁ + х₂ → max при ограничениях:

24.5. L( ) = x₁ + х₂ → max при ограничениях:

24.6. L( ) = 4x₁ + 5x₂ + x₃ → max при ограничениях:

24.7. L( ) = x₁ — 2x₂ + x₃ + 3x₄ → max при ограничениях:

24.8. Фирма выпускает три вида изделий А, Б, В, причем пла­новый сменный выпуск составляет 9 шт. изделия А, 7 шт. из­делия Б, 6 шт. изделия В.

Сменные ресурсы: 51 ед. производственного оборудования, 48 ед. сырья, 67 ед. электроэнергии, их расход на одно изделие дан в табл. 24.3.

Прибыль от реализации изделий А — 40 усл. ед., Б — 50 усл. ед., В — 10 усл. ед.

Определить, сколько изделий каждого вида надо произво­дить, чтобы получить максимальную прибыль от выпускае­мых сверх плана изделий.

24.9. Для приобретения оборудования по сортировке зерна фер­мер выделяет 34 усл. ед. Оборудование должно быть размеще­но на площади, не превышающей 60 м².

Фермер может заказать оборудование двух видов: менее мощные машины А стоимостью 3 усл. ед., требующие произ­водственной площади 3 м² (с учетом проходов) и обеспечиваю­щие производительность за смену 2 т зерна, и более мощные машины В стоимостью 4 усл. ед., занимающие площадь 5 м² и обеспечивающие за смену сортировку 3 т зерна.

Определить оптимальный вариант приобретения оборудо­вания, обеспечивающий фермеру при данных ограничениях максимум общей производительности сортировки, если он мо­жет приобрести не более 8 машин типа В.

24.10. Три типа самолетов следует распределить между че­тырьмя авиалиниями. В табл. 24.4 приведены данные месяч­ного объема перевозок каждым самолетом на каждой линии и соответствующих эксплуатационных расходов.

Распределить самолеты по линиям так, чтобы при мини­мальных суммарных эксплуатационных расходах перевезти по каждой из четырех авиалиний не менее 300, 200, 1000 и 500 ед. груза соответственно.