Экономический анализ задач с использованием графического метода

Проведем экономический анализ рассмотренной выше за­дачи по производству мороженого.

Математическая модель задачи имеет вид

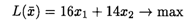
при ограничениях:

Согласно найденному оптимальному решению, фирме необ­ходимо выпускать в сутки 312,5 кг сливочного и 300 кг шоко­ладного мороженого, при этом максимально возможный доход составит 9 200 р.

Определим, как влияет на оптимальное решение увеличе­ние или уменьшение запасов исходных продуктов. Для анализа задачи примем, что неравенства системы ограничений могут быть активными или пассивными. Если прямая проходит че­рез точку, в которой находится оптимальное решение, то будем считать, что она представляет активное ограничение. В про­тивном случае прямая относится к пассивному ограничению.

Если ограничение активное, то будем считать, что соответ­ствующий ресурс является дефицитным, так как он использу­ется полностью. Если ограничение пассивное, то оно недефи­цитное и имеется в фирме в избытке.

Рассмотрим увеличение ресурса правой части ограничения (20.1) по молоку (рис. 20.2). При перемещении параллельно са­мой себе прямой (20.1) вправо до пересечения с прямыми (20.2) и (20.3) в точке М ограничение (20.1) будет оставаться актив­ным. Точку М определим как точку пересечения прямых (20.2) и (20.3):

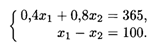
Откуда получаем М(370,83; 270,3).

Подставляя координаты точки М в уравнение (20.1), полу­чим предельно допустимый суточный запас молока:

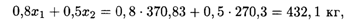
при этом величина дохода составляет

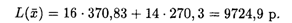
Рассмотрим увеличение ограничения по наполнителям (рис. 20.3). При перемещении параллельно самой себе прямой (20.2) вправо до пересечения с прямыми (20.1) и (20.4) в точ­ке N ограничение (20.2) будет оставаться активным. Точку N определим как точку пересечения прямых

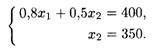
Откуда получаем N(281,25; 350).

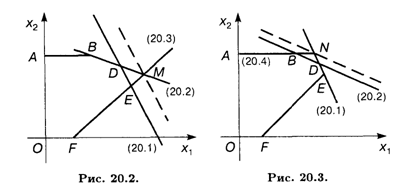
Предельно допустимый суточный запас наполнителей мож­но увеличивать до значения

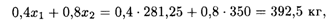
при этом величина дохода составит

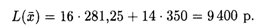
Рассмотрим возможность изменения правой части пассив­ных ограничений (20.3) и (20.4). Не изменяя оптимальное ре­шение (рис. 20.4), прямую (20.3) можно перемещать парал­лельно самой себе вверх до пересечения с точкой D(312,5; 300), т.е. правую часть ограничения (20.3) можно уменьшать до величины

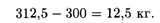
Прямую (20.3) можно перемещать параллельно самой себе вниз до пересечения с осью ОХ₁ в точке Р(500; 0), т.е. правую часть ограничения (20.3) можно увеличивать до 500 кг.

Таким образом, при неизменном оптимальном решении раз­ница в покупательском спросе на сливочное и шоколадное мо­роженое может изменяться в диапазоне от 12,5 до 500 кг.

Аналогично, не изменяя оптимальное решение (рис. 20.5), прямую (20.4) можно перемещать параллельно самой себе вверх до пересечения с осью ОХ₂ в точке R(0; 456,25) или вниз до пересечения с прямой (20.1) в точке D(312,5; 300).

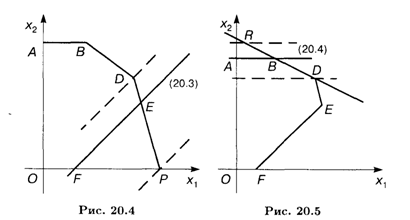
Таким образом, при неизменном оптимальном решении по­купательский спрос на шоколадное мороженое может изме­няться в диапазоне от 300 до 456,25 кг.

Проведем анализ задачи по пределам возможного измене­ния коэффициентов целевой функции, т.е. по диапазону опто­вых цен на мороженое, при котором не происходит изменения оптимального решения.

Изменение коэффициентов целевой функции оказывает вли­яние на наклон линии уровня. Уравнение линии уровня запи­сывается в общем виде (рис. 20.6):

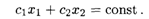
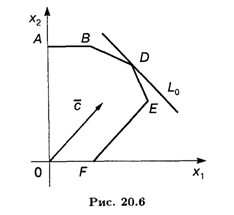
Угловой коэффициент прямой (20.1):

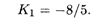
Так как прямые совпадают, то К = К₁, откуда c_1max = 22,4 при c₂ = 14. Коэффициент с₁ можно уменьшать до сов­падения линии уровня с прямой (20.2), поэтому

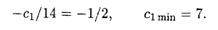
Таким образом, оптимальное решение задачи не изменится, ес­ли розничная цена 1 кг сливочного мороженого лежит в диапа­зоне от 7 до 22,4 р., при этом доход фирмы будет от 6 387,5 до 11200 р.

Аналогичные рассуждения для случая с₁ = 16 позволили сделать вывод, что оптимальное решение задачи не изменит­ся, если розничная цена 1 кг шоколадного мороженого лежит в диапазоне от 10 до 32 р., при этом доход фирмы будет от 8000 до 14 600 р.

УПРАЖНЕНИЯ

Решить задачи с использованием графического метода.

20.1. L() = 3x₁ + х₂→ max при ограничениях:

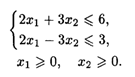
20.2. L() = 2x₁ — 10x₂ → min при ограничениях:

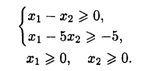
20.3. L() = 2x₁ + 3x₂ → max при ограничениях:

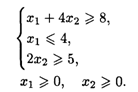
20.4. L() = 3x₁ + 5х₂→ max при ограничениях:

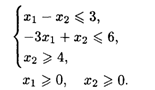
20.5. L() = 4x₁ + 6x₂ → min при ограничениях:

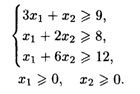
20.6. L() = 4x₂ → min при ограничениях:

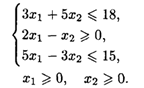
20.7. L() = 2x₁ + 3x₂ → max при ограничениях:

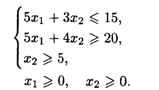
20.8. В суточный рацион включают два продукта питания П₁ и П₂, причем продукта П₁ должно войти в дневной рацион не более 200 ед. Стоимость 1 ед. продукта П₁ составляет 2 р., про­дукта П₂ — 4р. Содержание питательных веществ в 1 ед. про­дукта, минимальные нормы потребления указаны в табл. 20.2.

Определить оптимальный рацион питания, стоимость ко­торого будет наименьшей.

Провести анализ задач с использованием графического ме­тода.

20.9. L() = x₁ + x₂ → max (min) при ограничениях:

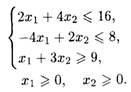
20.10. Фирма выпускает изделия двух типов: А и В. При этом используется сырье четырех видов. Расход сырья каждого вида на изготовление единицы продукции и запасы сырья заданы в табл 20.3.

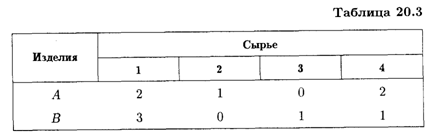
Запасы сырья 1-го вида составляют 21 ед., 2-го вида — 4 ед., 3-го вида — 6 ед. и 4-го вида — 10 ед. Выпуск одного из­делия типа А приносит доход 300 р., одного изделия типа В — 200р.

Составить план производства, обеспечивающий фирме наи­больший доход.

20.11. Обработка деталей А и В может производиться на трех станках, причем каждая деталь должна последовательно об­рабатываться на каждом из станков. Прибыль от реализации детали А — 100 р., детали В — 160 р. Исходные данные при­ведены в табл. 20.4.

Определить производственную программу, максимизирую­щую прибыль при условии: спрос на деталь А — не менее 300 шт., на деталь В — не более 200 шт.

Глава 21. СИМПЛЕКСНЫЙ МЕТОД

Общая постановка задачи

Метод является универсальным, так как позволяет решить практически любую задачу линейного программирования, за­писанную в каноническом виде.

Идея симплексного метода (метода последовательного улуч­шения плана) заключается в том, что начиная с некоторого исходного опорного решения осуществляется последовательно направленное перемещение по опорным решениям задачи к оп­тимальному. Значение целевой функции при этом перемеще­нии для задач на максимум не убывает. Так как число опорных решений конечно, то через конечное число шагов получим оп­тимальное опорное решение. Опорным решением называется базисное неотрицательное решение.