Продуктивные модели Леонтьева

Матрица А, все элементы которой неотрицательны, на­зывается продуктивной, если для любого вектора 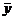с неот­рицательными компонентами существует решение уравнения (16.6) — вектор , все элементы которого неотрицательны. В таком случае и модель Леонтьева называется продуктивной.

Для уравнения типа (16.6) разработана соответствующая математическая теория исследования решения и его особеннос­тей. Укажем некоторые ее основные моменты. Приведем без доказательства важную теорему, позволяющую устанавливать продуктивность матрицы.

ТЕОРЕМА 16.1. Если для матрицы А с неотрицательными элементами и некоторого вектора 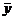с неотрицательными компонентами уравнение (16.6) имеет решение с неотри­цательными компонентами, то матрица А продуктивна.

Иными словами, достаточно установить наличие положи­тельного решения системы (16.6) хотя бы для одного положи­тельного вектора 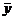, чтобы матрица А была продуктивной. Пе­репишем систему (16.6) с использованием единичной матрицы Е в виде

Если существует обратная матрица (E - А)^-1 , то существует и единственное решение уравнения (16.7):

Матрица (Е — А)^-1 называется матрицей полных затрат.

Существует несколько критериев продуктивности матри­цы А. Приведем два из них.

Первый критерий продуктивности. Матрица А продукти­вна тогда и только тогда, когда матрица (Е - А)^-1 сущест­вует и ее элементы неотрицательны.

Второй критерий продуктивности. Матрица А с неотри­цательными элементами продуктивна, если сумма элемен­тов по любому ее столбцу (строке) не превосходит единицы:

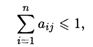
причем хотя бы для одного столбца (строки) эта сумма строго меньше единицы.

Рассмотрим применение модели Леонтьева на несложных примерах.

Пример 1. В табл. 16.4 приведены данные по балансу за не­который период времени между пятью отраслями промышлен­ности. Найти векторы конечного потребления и валового вы­пуска, а также матрицу коэффициентов прямых затрат и опре­делить, является ли она продуктивной в соответствии с при­веденными выше критериями.

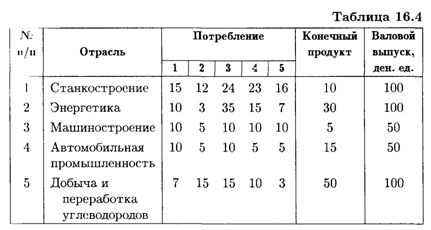
Решение. В данной таблице приведены составляющие ба­ланса в соответствии с соотношениями (16.2): x_ij — первые пять столбцов, у_i — шестой столбец, x_i — последний столбец (i,j = 1, 2, 3, 4, 5). Согласно формулам (16.3) и (16.4), имеем

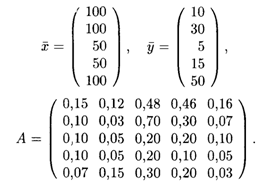
Все элементы матрицы А положительны, однако нетрудно видеть, что их сумма в третьем и четвертом столбцах боль­ше единицы. Следовательно, условия второго критерия продук­тивности не соблюдены и матрица А не является продуктив­ной. Экономическая причина этой непродуктивности заключа­ется в том, что внутреннее потребление отраслей 3 и 4 слиш­ком велико в соотношении с их валовыми выпусками.

Пример 2. Табл. 16.5 содержит данные баланса трех отрас­лей промышленности за некоторый период времени. Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление по отраслям увеличить соответственно до 60, 70 и 30 условных денежных единиц.

Решение. Выпишем векторы валового выпуска и конеч­ного потребления и матрицу коэффициентов прямых затрат. Согласно формулам (16.3) и (16.4), имеем

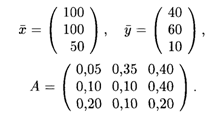
Матрица А удовлетворяет обоим критериям продуктивности. В случае заданного увеличения конечного потребления новый вектор конечного продукта будет иметь вид

Требуется найти новый вектор валового выпуска _*, удов­летворяющий соотношениям баланса в предположении, что матрица А не изменяется. В таком случае компоненты x₁, x₂, х₃ неизвестного вектора _* находятся из системы уравнений, которая согласно (16.4) имеет в данном случае вид

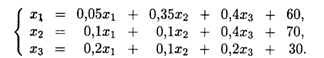
В матричной форме эта система выглядит следующим об­разом:

или

где матрица (Е — А) имеет вид

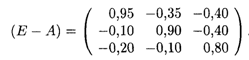
Решение системы линейных уравнений (16.11) при заданном векторе правой части (16.9) (например, методом Гаусса) да­ет новый вектор _* как решение системы уравнений баланса (16.10):

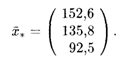
Таким образом, для того чтобы обеспечить заданное уве­личение компонент вектора конечного продукта, необходимо увеличить соответствующие валовые выпуски: добычу и пе­реработку углеводородов на 52,2%, уровень энергетики — на 35,8% и выпуск продукции машиностроения — на 85% по срав­нению с исходными величинами, указанными в табл. 16.5.

Линейная модель торговли

Одним из примеров экономического процесса, приводящего к понятию собственного числа и собственного вектора матри­цы, является процесс взаимных закупок товаров. Будем пола­гать, что бюджеты п стран, которые мы обозначим соответ­ственно x₁, x₂, … , x_n расходуются на покупку товаров. Мы будем рассматривать линейную модель обмена, или, как ее еще называют, модель международной торговли.

Пусть a_ij — доля бюджета x_j, которую j-я страна тратит на закупку товаров у i-й страны. Введем матрицу коэффици­ентов a_ij:

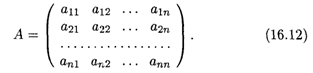
Тогда если весь бюджет расходуется только на закупки внутри страны и вне ее (можно это трактовать как торговый бюджет), то справедливо равенство

Матрица (16.12) со свойством (16.13), в силу которого сум­ма элементов ее любого столбца равна единице, называется структурной матрицей торговли. Для i-й страны общая вы­ручка от внутренней и внешней торговли выражается форму­лой

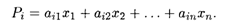
Условие сбалансированной (бездефицитной) торговли фор­мулируется естественным образом: для каждой страны ее бюд­жет должен быть не больше выручки от торговли, т.е. P_i ≥ x_i:, или

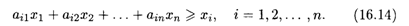
Докажем, что в условиях (16.14) не может быть знака не­равенства. Действительно, сложим все эти неравенства при i от 1 до n. Группируя слагаемые с величинами бюджетов x_j, получаем

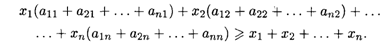
Нетрудно видеть, что в скобках стоят суммы элементов матри­цы А по ее столбцам от первого до последнего, которые равны единице по условию (16.13). Стало быть, мы получили нера­венство

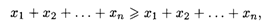
откуда возможен только знак равенства.

Таким образом, условия (16.14) принимают вид равенств:

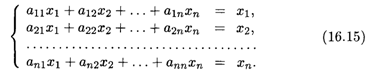
Введем вектор бюджетов , каждая компонента которого ха­рактеризует бюджет соответствующей страны; тогда систему уравнений (16.15) можно записать в матричной форме

Это уравнение означает, что собственный вектор структурной матрицы А, отвечающий ее собственному значению λ = 1, со­стоит из бюджетов стран бездефицитной международной тор­говли.

Перепишем уравнение (16.16) в виде, позволяющем опреде­лить :

Пример. Структурная матрица торговли четырех стран име­ет вид:

Найти бюджеты этих стран, удовлетворяющие сбалансиро­ванной бездефицитной торговле при условии, что сумма бюд­жетов задана:

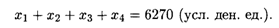
Решение. Необходимо найти собственный вектор , отве­чающий собственному значению λ = 1 заданной структурной матрицы А, т.е. решить уравнение (16.17), которое в нашем случае имеет вид

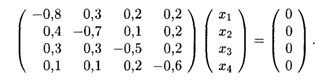
Поскольку ранг этой системы равен трем, то одна из неизвест­ных является свободной переменной и остальные выражаются через нее. Решая систему методом Гаусса, находим компонен­ты собственного вектора :

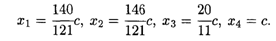
Подставив найденные значения в заданную сумму бюджетов, найдем величину с: с = 1210, откуда окончательно получаем искомые величины бюджетов стран при бездефицитной торговле (в условных денежных единицах):

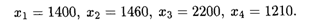
УПРАЖНЕНИЯ

16.1. По данным табл. 16.1 составить новую таблицу про­изводственно-экономических показателей по следующим усло­виям:

— количество изделий всех видов увеличивается на 20%,

— норма времени изготовления по всем изделиям уменьша­ется на 20%,

— цена на все виды изделий уменьшается на 10%.

Найти ежесуточные показатели, указанные в задаче 1 п. 16.1, а также их процентные изменения.

16.2. По данным табл. 16.2 составить новую таблицу по сле­дующим условиям:

— дневная производительность всех предприятий увеличи­вается на 100%,

— число рабочих дней в году для 1-го предприятия увели­чивается на 50%, а для остальных — на 40%,

— цены на виды сырья уменьшаются соответственно на 10, 20 и 30%.

Определить суммы кредитования предприятий и их соот­ветствующие процентные изменения.

16.3. Отрасль состоит из 4-х предприятий; вектор выпуска продукции и матрица внутреннего потребления имеют вид

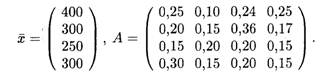
Найти вектор объемов конечного продукта, предназначенного для реализации вне отрасли.

16.4. Предприятие выпускает три вида продукции с использованием трех видов сырья, характеристики производства указаны в следующей таблице:

Найти объем выпуска продукции каждого вида при заданных запасах сырья.

16.5. В условиях примера 2 п. 16.2 определить прирост объе­мов валовых выпусков по каждой отрасли (в процентах), если конечное потребление увеличить по отраслям соответственно на 30, 10 и 50%. Решить задачу методом обратной матрицы и методом Гаусса.

16.6. Структурная матрица торговли трех стран имеет вид

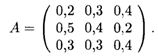
Найти бюджеты первой и второй стран, удовлетворяющие сба­лансированной бездефицитной торговле при условии, что бюд­жет третьей страны равен 1100 усл. ед.