Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами)

Рассмотрим модель рынка с прогнозируемыми ценами. В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Однако спрос и предложение в реальных ситуациях зависят еще и от тен­денции ценообразования и темпов изменения цены. В моделях с непрерывными и дифференцируемыми по времени t функци­ями эти характеристики описываются соответственно первой и второй производными функции цены P(t).

Рассмотрим конкретный пример. Пусть функции спроса D и предложения S имеют следующие зависимости от цены Р и ее производных:

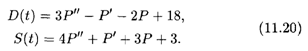
Принятые в (11.20) зависимости вполне реалистичны: поясним это на слагаемых с производными функции цены.

1. Спрос "подогревается" темпом изменения цены: если темп растет (Р" > 0), то рынок увеличивает интерес к то­вару, и наоборот. Быстрый рост цены отпугивает покупателя, поэтому слагаемое с первой производной функции цены входит со знаком минус.

2. Предложение в еще большей мере усиливается темпом изменения цены, поэтому коэффициент при Р" в функции S(t) больше, чем в D(t). Рост цены также увеличивает предложе­ние, потому слагаемое, содержащее Р', входит в выражение для S(t) со знаком плюс.

Требуется установить зависимость цены от времени. По­скольку равновесное состояние рынка характеризуется равен­ством D = S, приравняем правые части уравнений (11.20). После приведения подобных получаем

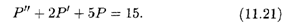
Соотношение (11.21) представляет линейное неоднородное дифференциальное уравнение второго порядка относительно функции P(t). Как было установлено в п. 10.3, общее решение такого уравнения состоит из суммы какого-либо его частно­го решения и общего решения соответствующего однородного уравнения

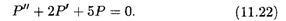
Характеристическое уравнение имеет вид

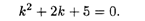
Его корни — комплексно-сопряженные числа: k_1,2 = -1 ± 2i, и, следовательно, общее решение уравнения (11.22) дается фор­мулой

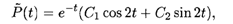
где С₁ и С₂ — произвольные постоянные. В качестве частно­го решения неоднородного уравнения (11.21) возьмем решение Р = P_st — постоянную величину как установившуюся цену. Подстановка в уравнение (11.21) дает значение P_st:

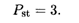
Таким образом, общее решение уравнения (11.21) имеет вид

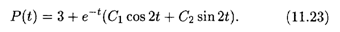
Нетрудно видеть, что P(t) P_st = 3 при t , т.е. все интегральные кривые имеют горизонтальную асимптоту Р = 3 и колеблются около нее. Это означает, что все цены стремятся к установившейся цене P_st с колебаниями около нее, причем амплитуда этих колебаний затухает со временем.

Приведем частные решения этой задачи в двух вариантах: задача Коши и смешанная задача.

1. Задача Коши. Пусть в начальный момент времени из­вестна цена, а также тенденция ее изменения:

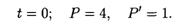
Подставляя первое условие в формулу (11.23), получаем Р(0) = С₁ + 3 = 4, откуда С₁ = 1, т.е. имеем

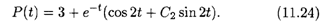
Дифференцируя, имеем отсюда

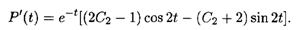
Теперь реализуем второе условие задачи Коши: Р'(0) = 2C₂ — 1=1, откуда C₂ = 1. Окончательно получаем, что решение задачи Коши имеет вид

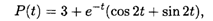
или в более удобной форме:

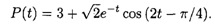
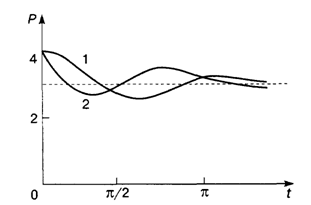
Рис.11.5

2. Смешанная задача. Пусть в начальный момент времени известны цена и спрос:

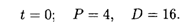
Поскольку первое начальное условие такое же, как и в преды­дущем случае, то имеем и здесь решение (11.24). Тогда произ­водные функции Р(t) выражаются формулами

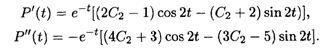
Отсюда Р'(0) =2C₂ - 1и Р"(0) = -4C₂ - 3. Подставляя эти равенства во второе условие задачи, т.е. D(0) = 16, имеем с учетом вида D(t) из первой формулы (11.20): С₂ = -1. Итак, решение данной задачи имеет вид

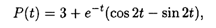
или в более удобной форме:

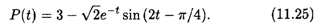
Интегральные кривые, соответствующие задачам 1 и 2, изоб­ражены на рис. 11.5.

УПРАЖНЕНИЯ

11.1. Используя формулу (11.13) динамики национального до­хода Y(t) по модели Кейнса,

а) проанализировать роль каждого параметра в увеличе­нии величины Y_р согласно формуле (11.12), что ведет к паде­нию Y(t);

б) вывести рекомендации по изменению параметров, опи­сывающих основные экономические показатели;

в) выбрать более предпочтительные изменения, указанные в п. б, применительно к условиям России.

11.2. Найти динамику цены Р на товар, если прогноз спроса и предложения описывается следующими соотношениями:

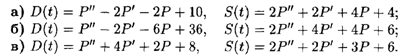
11.3. В условиях предыдущей задачи какой из трех случаев описывает паническое состояние на рынке и с чем это связано?