Вещественные числа и их свойства

Множество вещественных чисел является бесконечным.Оносостоит из рациональных и иррациональных чисел. Рациональ­ным называется число вида p/q, где р и q — целые числа. Вся­кое вещественное число, не являющееся рациональным, назы­вается иррациональным. Всякое рациональное число либо является целым, либо представляет собой конечную или пери­одическую бесконечную десятичную дробь. Например, рацио­нальное число 1/9 можно представить в виде 0,11111.... Иррациональное число представляет собой бесконечную неперио­дическую десятичную дробь; примеры иррациональных чисел:

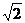= 1,41421356...; 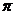= 3,14159265....

Сведения о вещественных числах могут быть кратко сис­тематизированы в виде перечисления их свойств.

А. Сложение и умножение вещественных чисел

Для любой пары вещественных чисел а и b определены единственным образом два вещественных числа а + b и а ∙ b, называемые соответственно их суммой и произведением. Для любых чисел а,b и с имеют место следующие свойства.

1. a + b = b + а, а ∙ b = b ∙ а (переместительное свойство).

2. а + (b + с) = (а + b) + с, а ∙ (b ∙ с) = (а ∙ b) ∙ с (сочетательное свойство).

3. (а + b) ∙ с = а ∙ с + b ∙ с (распределительное свойство).

4. Существует единственное число 0, такое, что а + 0 = a для любого числа а.

5. Для любого числа а существует такое число (-а),что а + (-а) = 0.

6. Существует единственное число 1 ≠ 0, такое, что для любого числа а имеет место равенство

а ∙ 1 = a.

7. Для любого числа а ≠ 0 существует такое число а^-1, что а ∙ а^-1 = 1. Число а^-1 обозначается также символом .

В. Сравнение вещественных чисел

Для любых двух вещественных чисел имеет место одно из трех соотношений: а = b (а равно b), а > b (а больше b) или а < b (а меньше b). Отношение равенства обладает свойством транзитивности: если а = b и b = с, то а = с.

Отношение "больше" обладает следующими свойствами.

8. Если а > b и b > с, то а > с.

9. Если а > b, то а + с > b + с.

10. Если а > 0 и b > 0, тоа b > 0

Вместо соотношения а > b употребляют также b < а. Запись а ≥ b (b ≤ а) означает, что либо а = b, либо a > b. Соотношения со знаками>, <,≥ и ≤ называютcя неравенствами, причем соотношения типа 8 < 10 —строгими неравенствами.

11. Любое вещественное число можно приблизить рацио­нальными числами с произвольной точностью.

С. Непрерывность вещественных чисел.

12. Пусть Х и Y — два множества вещественных чисел. Тогда, если для любых чисел 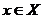и 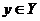выполняется неравенство х ≤ у, то существует хотя бы одно число с, такое, что для всех х и у выполняются нера­венства х ≤ с ≤ у.

Отметим здесь, что свойством непрерывности обладает множество всех вещественных (действительных) чисел, но не обладает множество, состоящее только из рациональных чисел.

Таким образом, вещественные числа представляют собой множество элементов, обладающих свойства­ми А-С. Такое определение, из которого выводятся ос­тальные свойства, называется аксиоматическим, а сами свойства А-С — аксиомами вещественных чисел.