Рациональные и вещественные числа.
Понятие вещественного (действительного) числа принадлежит к основным математическим понятиям. Существуют различные подходы к определению вещественного числа (метод сечений, определение вещественного числа как бесконечной десятичной дроби и др.), однако наиболее логичным и простым является аксиоматический метод введения вещественного числа. Заметим, что все методы введения вещественного числа эквивалентны, так как ни в одном из них не устанавливается факт существования вещественного числа. Поэтому во всех случаях необходимо вводить аксиому существования вещественного числа. Поскольку же использование аксиом неизбежно, проще всего их сразу сформулировать.
Бесконечной десятичной дробью называется последовательность чисел 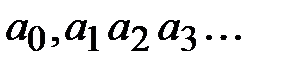 , перед которой поставлен знак плюс или минус, где
, перед которой поставлен знак плюс или минус, где 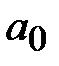 – натуральное число,
– натуральное число, 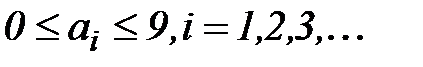 ..
..
Если перед дробью стоит знак минус, то дробь называется отрицательной, в противном случае дробь называется неотрицательной. Знак плюс перед дробью можно не ставить.
Десятичная дробь 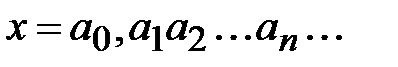
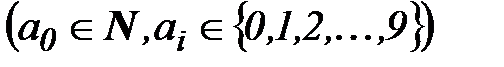 называется конечной, если
называется конечной, если 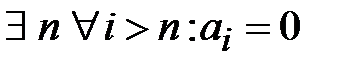 .
.
Конечную десятичную дробь будем записывать в виде:  .
.
Вспомним, что бесконечная десятичная дробь является периодической, если 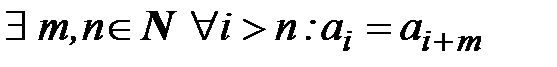 . Например, 2,357474…=2,35(74), здесь
. Например, 2,357474…=2,35(74), здесь 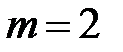 , Заметим, что конечная десятичная дробь есть частный случай периодической дроби.
, Заметим, что конечная десятичная дробь есть частный случай периодической дроби.
Рациональным числом называется число, которое может быть представлено в виде отношения двух целых чисел, т.е. p/q, причем q≠0. Всякое рациональное число может быть представлено либо конечной десятичной дробью, либо периодической дробью. Например, рациональные числа 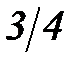 и 1/3 можно представить в виде следующих десятичных дробей:
и 1/3 можно представить в виде следующих десятичных дробей: 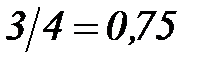 ; 1/3=0,3333…Множество рациональных чисел обозначим
; 1/3=0,3333…Множество рациональных чисел обозначим 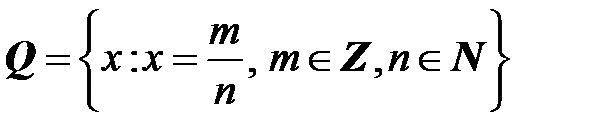 .
.
Таким образом, все множество бесконечных десятичных дробей состоит из конечных десятичных дробей, из бесконечных периодических и из бесконечных непериодических дробей. Бесконечные непериодические десятичные дроби называются иррациональными числами. Например, иррациональные числа 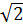 и π можно представить в виде следующих десятичных дробей:
и π можно представить в виде следующих десятичных дробей: 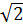 =1,41431356…., π=3,14159…. Рациональные и иррациональные числа образуют множество чисел, которое называется множеством вещественных чисел или действительных чисел и обозначается R.
=1,41431356…., π=3,14159…. Рациональные и иррациональные числа образуют множество чисел, которое называется множеством вещественных чисел или действительных чисел и обозначается R.
Здесь можно также отметить, что все действительные числа также подразделяются на алгебраические числа и трансцендентные числа. Число называется алгебраическим, если оно является корнем алгебраического многочлена с целыми коэффициентами, причем, если у этого многочлена коэффициент при старшей степени равен единице, то данное число называется целым алгебраическим числом. Очевидно, что к алгебраическим числам относятся все рациональные числа. Если же число не является алгебраическим, то оно называется трансцедентным.
Приведем основные свойства вещественных чисел, которые примем за аксиомы.
 Сложение и умножение вещественных чисел.
Сложение и умножение вещественных чисел.
Для любой пары a и b вещественных чисел определены, и притом единственным образом, два вещественных числа 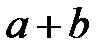 и
и 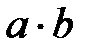 , называемые их суммой и произведением, обладающими следующими свойствами. Каковы бы ни были числа a, b и c:
, называемые их суммой и произведением, обладающими следующими свойствами. Каковы бы ни были числа a, b и c:
1. 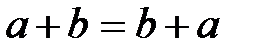 (переместительное свойство или коммутативность сложения).
(переместительное свойство или коммутативность сложения).
2. 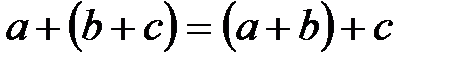 (сочетательное свойство или ассоциативность сложения).
(сочетательное свойство или ассоциативность сложения).
3. 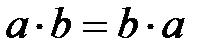 (переместительное свойство или коммутативность умножения).
(переместительное свойство или коммутативность умножения).
4. 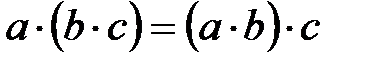 (сочетательное свойство или ассоциативность умножения).
(сочетательное свойство или ассоциативность умножения).
5. 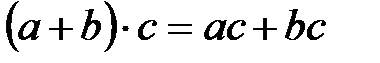 (распределительное свойство или дистрибутивность).
(распределительное свойство или дистрибутивность).
6. Существует единственное число 0 такое, что 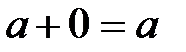 для любого числа a.
для любого числа a.
7. Для любого числа a существует такое число 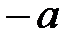 , что
, что 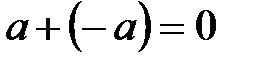 .
.
8. Существует единственное число 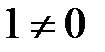 такое, что для любого числа а имеет место равенство
такое, что для любого числа а имеет место равенство 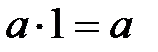 .
.
9. Для любого числа 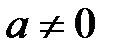 существует такое число
существует такое число 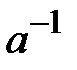 , что
, что 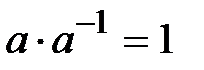 ; число
; число 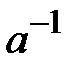 обозначается также символом
обозначается также символом 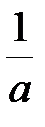 .
.
Замечание. Числа 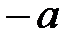 и
и 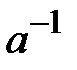 , в свойствах 7 и 9, единственны. В самом деле, если бы существовало еще одно число
, в свойствах 7 и 9, единственны. В самом деле, если бы существовало еще одно число 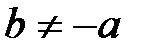 , удовлетворяющее условию
, удовлетворяющее условию 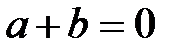 , то
, то 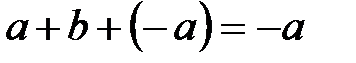 , откуда
, откуда 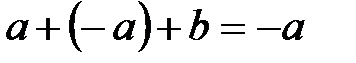 ,
, 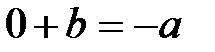 и
и 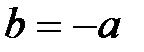 . Получено противоречие.
. Получено противоречие.
 Сравнение вещественных чисел.
Сравнение вещественных чисел.
Для любых двух вещественных чисел a и b установлено одно из отношений: 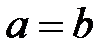 (a равно b),
(a равно b), 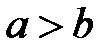 или
или 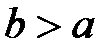 (a больше b или b больше а). Отношение = обладает свойством: если
(a больше b или b больше а). Отношение = обладает свойством: если 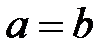 и
и 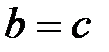 , то
, то 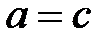 .
.
Вместо отношения 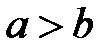 пишут также
пишут также 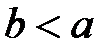 (b меньше a). Запись вида
(b меньше a). Запись вида 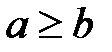 (или, что то же,
(или, что то же, 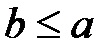 ) обозначает, что либо
) обозначает, что либо 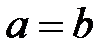 , либо
, либо 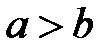 . Соотношения
. Соотношения 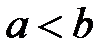 ,
, 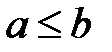 ,
, 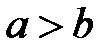 ,
, 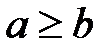 называются неравенствами. Неравенства
называются неравенствами. Неравенства 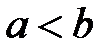 и
и 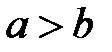 называются строгими неравенствами.
называются строгими неравенствами.
Число а, удовлетворяющее неравенству 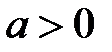 , называется положительным, а число a, удовлетворяющее неравенству
, называется положительным, а число a, удовлетворяющее неравенству 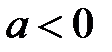 , – отрицательным.
, – отрицательным.
Отношения >, < обладают следующими свойствами.
10. Если 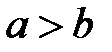 и
и 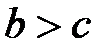 , то
, то  (транзитивность).
(транзитивность).
11. Если 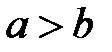 , то
, то 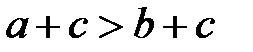 (к обеим частям неравенства можно прибавлять любое число и при этом знак неравенства не изменяется).
(к обеим частям неравенства можно прибавлять любое число и при этом знак неравенства не изменяется).
12. Если 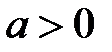 и
и 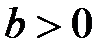 , то
, то 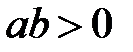 .
.
13.Если 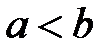 , то
, то 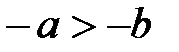 (при умножении неравенства на отрицательное число знак неравенства изменяется на противоположный) .
(при умножении неравенства на отрицательное число знак неравенства изменяется на противоположный) .
14. Если 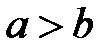 и
и 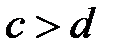 , то
, то 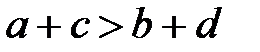 (неравенства одного знака можно почленно складывать).
(неравенства одного знака можно почленно складывать).
 Непрерывность вещественных чисел
Непрерывность вещественных чисел
15. Пусть X и Y – два множества, состоящие из вещественных чисел. Тогда, если для любых чисел 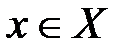 и
и 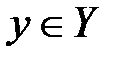 выполняется неравенство
выполняется неравенство 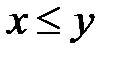 , то существует хотя бы одно число c, такое, что для любых чисел x и y выполняются неравенства
, то существует хотя бы одно число c, такое, что для любых чисел x и y выполняются неравенства
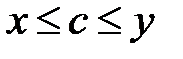 .
.
Следует заметить, что свойством непрерывности обладает множество всех вещественных чисел, но им не обладает множество только рациональных чисел. Действительно, пусть множество X состоит из рациональных чисел x, для которых выполняется неравенство 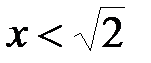 , а множество Y состоит из рациональных чисел y, для которых выполняется неравенство
, а множество Y состоит из рациональных чисел y, для которых выполняется неравенство 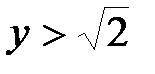 . Тогда, очевидно, для любого числа
. Тогда, очевидно, для любого числа 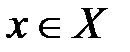 и любого числа
и любого числа 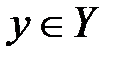 выполняется неравенство
выполняется неравенство 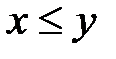 . Однако, не существует рационального числа c такого, чтобы выполнялись неравенства
. Однако, не существует рационального числа c такого, чтобы выполнялись неравенства 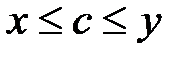 . В самом деле, таким числом могло бы быть только
. В самом деле, таким числом могло бы быть только 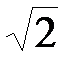 , которое, но оно не является рациональным.
, которое, но оно не является рациональным.
Теперь окончательно будем считать, что вещественные числа представляют собой множество элементов, обладающих свойствами 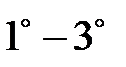 . Такое определение вещественных чисел называется аксиоматическим, а свойства
. Такое определение вещественных чисел называется аксиоматическим, а свойства 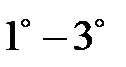 аксиомами вещественных чисел.
аксиомами вещественных чисел.
В дальнейшем будем иметь дело с различными множествами вещественных чисел. Всюду, где это не может привести к неточности, для краткости вещественные числа будем называть просто числами.
Если 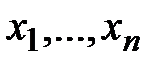 – произвольные числа, то запись
– произвольные числа, то запись 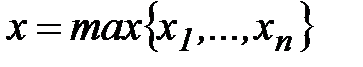
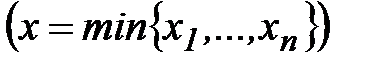 означает, что число x максимальное (минимальное) из чисел
означает, что число x максимальное (минимальное) из чисел 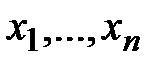 .
.

Установим взаимно-однозначное соответствие между точками бесконечной направленной прямой и множеством вещественных чисел. Пусть 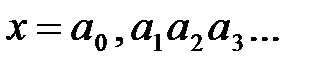 , где
, где
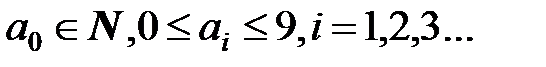 .Рассмотрим направленную прямую, на которой указаны две точки О и Е. Точка О – начало отчета, отрезок ОЕ – масштабный отрезок. Точке О поставим в соответствии число
.Рассмотрим направленную прямую, на которой указаны две точки О и Е. Точка О – начало отчета, отрезок ОЕ – масштабный отрезок. Точке О поставим в соответствии число 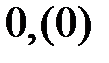 , которое называется нулем.
, которое называется нулем.
а) Сначала произвольной точке М поставим в соответствии определенное вещественное число, указав каким образом будет выписываться (строиться) бесконечная десятичная дробь 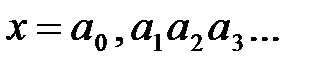 которая соответствует точке М.
которая соответствует точке М.
Пусть точка Е лежит справа от 0. Будем рассматривать точку М, лежащую лишь справа от точки О, т.к. точкам, которые лежат слева будут соответствовать отрицательные вещественные числа, десятичные знаки которых определены так же, как и для точек справа от О.
Число a0 положим равным максимальному числу отрезков ОЕ, которые укладываются внутри отрезка ОМ. Если остатка не получается, то полагаем 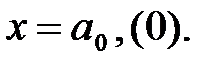 Если отрезок ОЕ укладывается внутри отрезка OM и остается отрезок
Если отрезок ОЕ укладывается внутри отрезка OM и остается отрезок 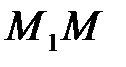 меньший, чем ОЕ, то цифру
меньший, чем ОЕ, то цифру 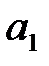 , выбираем как наибольшее число отрезков
, выбираем как наибольшее число отрезков 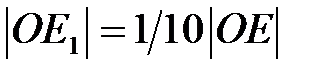 , целиком укладывающихся внутри
, целиком укладывающихся внутри 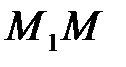 .
.
Если после этого не получается остатка, то полагаем 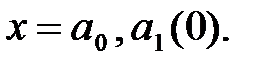 Если получается остаток
Если получается остаток 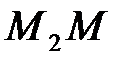 , то цифру
, то цифру 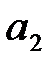 находим, сравнивая длину отрезка
находим, сравнивая длину отрезка 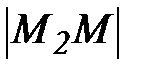 с отрезком
с отрезком 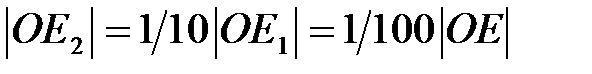 . Продолжая этот процесс, получим бесконечную десятичную дробь
. Продолжая этот процесс, получим бесконечную десятичную дробь 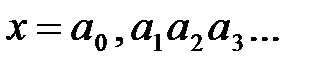 , соответствующую точке М.
, соответствующую точке М.
Таким образом, любой произвольной точке численной прямой поставлено в соответствие вещественное число х. Легко проверить, что двум различным точкам прямой будут соответствовать два различных числа или две различные десятичные дроби.
б) Теперь покажем обратное, что любому вещественному числу соответствует некоторая точка М направленной прямой. Воспользуемся аксиомой Кантора: для любой последовательности вложенных отрезков 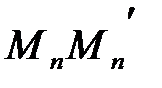 :
:

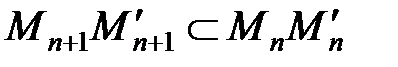
на прямой существует хотя бы одна точка М, принадлежащая всем отрезкам 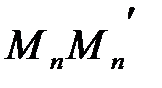 .
.
Пусть 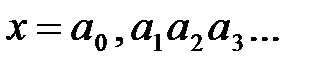 произвольное положительное вещественное число, а
произвольное положительное вещественное число, а 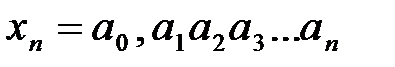 и
и 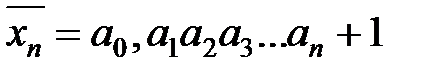 две конечные десятичные дроби, т.е. два рациональных числа, удовлетворяющих неравенству:
две конечные десятичные дроби, т.е. два рациональных числа, удовлетворяющих неравенству: 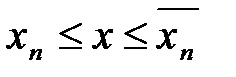 . Числа
. Числа 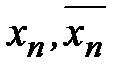 называются нижним и верхним n-значными приближениями числа x.
называются нижним и верхним n-значными приближениями числа x.
Рациональное число 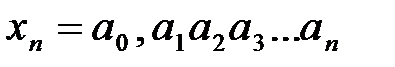 соответствует точке
соответствует точке 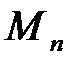 прямой ОЕ, которое определяется следующим условием:
прямой ОЕ, которое определяется следующим условием:

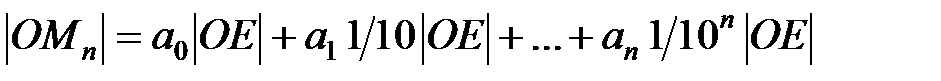 .
.
Точно также рациональное число 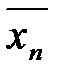 соответствующее точке
соответствующее точке 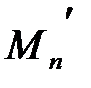 .Т.к.
.Т.к. 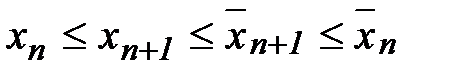 , то отрезки
, то отрезки 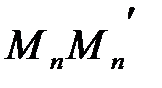 вложены друг в друга. В силу аксиомы Кантора существует точка М, которая принадлежит всем отрезкам одновременно. В силу построенного выше соответствия образом точки М будет вещественное число
вложены друг в друга. В силу аксиомы Кантора существует точка М, которая принадлежит всем отрезкам одновременно. В силу построенного выше соответствия образом точки М будет вещественное число 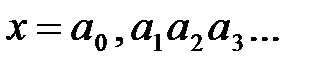 .
.
Следовательно, построено взаимно однозначное соответствие между множеством действительных чисел и множеством точек на прямой линии. Прямая линия, на которой откладываются вещественные числа, называется числовой прямой. Ясно, что точке О соответствует число 0, а точке Е – число 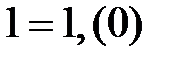 .
.
1.3. Ограниченные подмножества множества R
Пусть 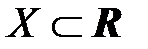 , т.е. Х - подмножество множества вещественных чисел.
, т.е. Х - подмножество множества вещественных чисел.
Определение 14. Множество Х называют ограниченным сверху (снизу), если существует число 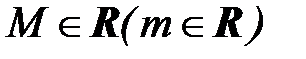 такое, что
такое, что 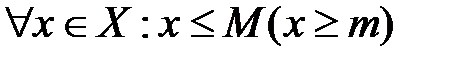 . Числа М и m называются верхней и нижней гранью множества Х.
. Числа М и m называются верхней и нижней гранью множества Х.
Определение 15. Множество Х называется ограниченным, если оно ограничено и сверху и снизу:
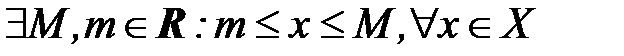
Ясно, что как верхних, так и нижних граней у множества может быть бесконечно много.
Определение ограниченного множества Х можно записатьи так: 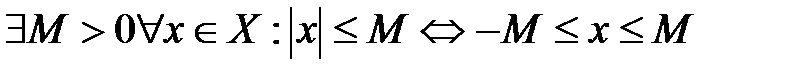 .
.
Приведем наиболее употребляемые числовые множества. Пусть 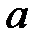 и
и 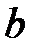 – два числа, причем
– два числа, причем 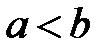 . Будем использовать следующие обозначения:
. Будем использовать следующие обозначения:
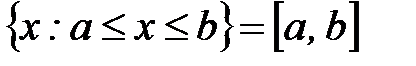 - отрезок;
- отрезок;
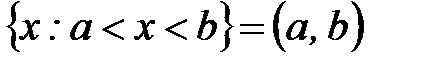 - интервал;
- интервал;
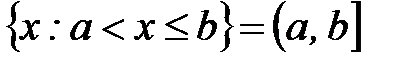 ;
; 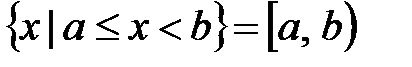 - полуинтервалы;
- полуинтервалы;
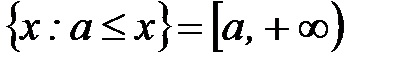 ;
; 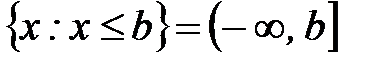 - лучи;
- лучи;
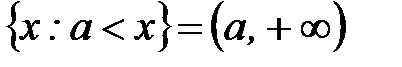 ;
; 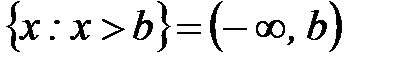 - лучи.
- лучи.
R= 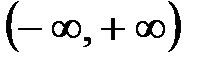 - множество вещественных чисел
- множество вещественных чисел
Все эти множества будем называть промежутками и обозначать X. Промежутки 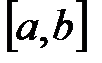 ,
, 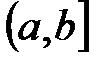 ,
, 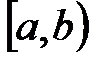 и
и 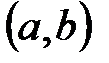 называются конечными;
называются конечными; 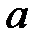 и
и 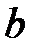 – их концы. Остальные промежутки называются бесконечными.
– их концы. Остальные промежутки называются бесконечными.
Интервал 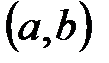 отличается от отрезка
отличается от отрезка 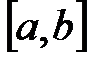 лишь тем, что ему не принадлежат концы
лишь тем, что ему не принадлежат концы 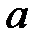 и
и 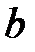 . Это отличие играет существенную роль во многих вопросах математического анализа. Кроме того, интервал
. Это отличие играет существенную роль во многих вопросах математического анализа. Кроме того, интервал 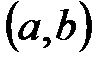 не содержит ни наибольшего, ни наименьшего числа, в то время как в отрезке
не содержит ни наибольшего, ни наименьшего числа, в то время как в отрезке 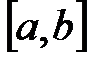 такими числами являются соответственно
такими числами являются соответственно 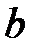 и
и 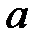 . Примером промежутка является
. Примером промежутка является 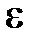 - окрестность точки
- окрестность точки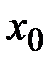 ,это множество
,это множество 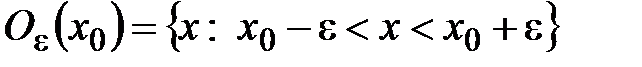 , где
, где 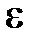 некоторое положительное число.
некоторое положительное число.
Определение 16. Наименьшее среди всех чисел, ограничивающих сверху множество Х, называется точной верхней гранью и обозначается 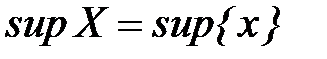 . Наибольшее среди всех чисел, ограничивающих снизу множество Х, называется точной нижней гранью и обозначается
. Наибольшее среди всех чисел, ограничивающих снизу множество Х, называется точной нижней гранью и обозначается 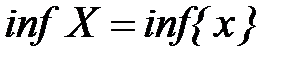 .
.
Заметим, что в определении не говорится, что существует или нет наименьшее или наибольшее число среди всех чисел, ограничивающих сверху или снизу данное множество. Также из определения ясно, если нижняя и верхняя грань существует, то она единственная, т.к. на всяком множестве чисел существует единственное наименьшее или наибольшее число. Можно дать эквивалентное символическое определение.
Определение 17. Число 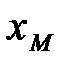 называется точной верхней гранью множества Х, если выполняются условия:
называется точной верхней гранью множества Х, если выполняются условия:
1) 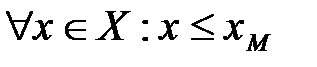 ;
;
2) 
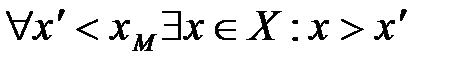
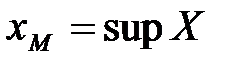
Число 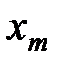 называется точной нижней гранью множества Х, если выполняются условия:
называется точной нижней гранью множества Х, если выполняются условия:
1) 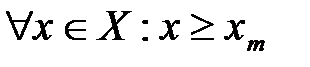 ;
;
2) 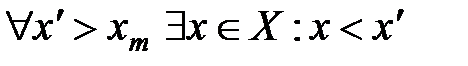

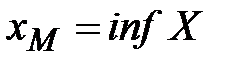
Легко проверить эквивалентность определений 16 и 17. Докажем для supХ:
а) Пусть 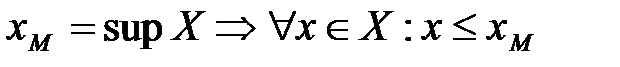 (по определению 16). Пусть
(по определению 16). Пусть 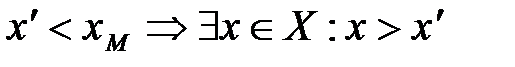 , т.к. в противном случае
, т.к. в противном случае 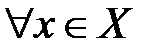 выполнялось бы
выполнялось бы 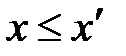 и число
и число 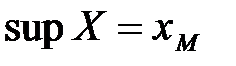 не было бы наименьшей верхней гранью.
не было бы наименьшей верхней гранью.
б) Пусть условие 2) выполняется, тогда в силу 1) 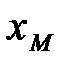 есть верхняя грань, в силу 2)
есть верхняя грань, в силу 2) 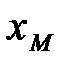 есть наименьшая верхняя грань.
есть наименьшая верхняя грань.
Замечание.Условие 2) можно заменить следующим:
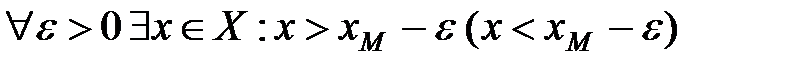 .
.
Действительно, это следует из замены: 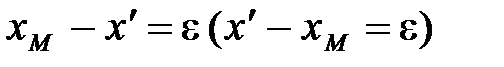 .
.
Точные грани могут принадлежать и могут не принадлежать множеству. Например:
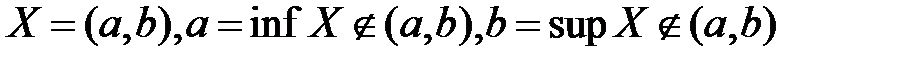 ;
;
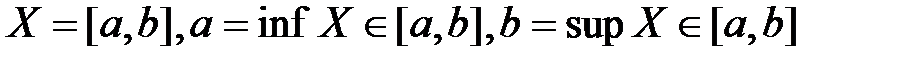 .
.
Справедливо следующее очень важная теорема, которую оставим без доказательства
Теорема 1.Пусть Х некоторое подмножество множества действительных чисел. Тогда, если Х ограничено сверху, то существует точная верхняя грань sup Х множества X. Если Х ограничено снизу, то существует точная нижняя грань inf Х множества X .
□ Пусть 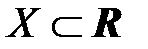 непустое, ограниченное сверху множество. Тогда множество
непустое, ограниченное сверху множество. Тогда множество 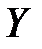 чисел, ограничивающих множество X сверху не пусто. Из определения верхней грани следует, что для любого
чисел, ограничивающих множество X сверху не пусто. Из определения верхней грани следует, что для любого 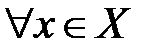 и
и 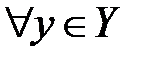 имеет место неравенство
имеет место неравенство 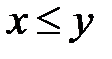 . В силу свойства непрерывности такое число с, что для любых
. В силу свойства непрерывности такое число с, что для любых 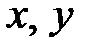 выполняется неравенство
выполняется неравенство 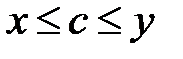 .
.
Из левой части этого неравенства следует, что число с ограничивает X, т.е. является верхней гранью. Из правой части следует, что оно является точной верхней гранью. ■
Теперь сформулируем несколько важных понятий, которые потребуются в дальнейшем.
Определение 18. Точка х называется предельной точкой множества Х, если любая её сколь угодно малая 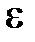 - окрестность содержит хотя бы одну точку х’ отличную от х.Определение 19. Точка х, принадлежащая множеству Х, называется изолированной точкой х, если она не является предельной точкой этого множества.
- окрестность содержит хотя бы одну точку х’ отличную от х.Определение 19. Точка х, принадлежащая множеству Х, называется изолированной точкой х, если она не является предельной точкой этого множества.
Определение 20. Точка х называется внутренней точкой множества Х, если она принадлежит этому множеству вместе с некоторой своей окрестностью.
Пример. В множестве 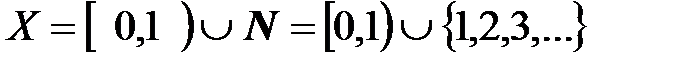 точки 2, 3,… - являются изолированными точками, 1 – предельная точка, 0 – предельная точка, любые точки интервала [0;1) – предельные. Точки 1 и 0 не внутренние, а точки из интервала (0;1) внутренние.
точки 2, 3,… - являются изолированными точками, 1 – предельная точка, 0 – предельная точка, любые точки интервала [0;1) – предельные. Точки 1 и 0 не внутренние, а точки из интервала (0;1) внутренние.
Определение 21. Множество Х называется замкнутым, если оно содержит все свои предельные точки.
Определение 22.Множество Х называется открытым, если каждая его точка внутренняя.
Пример. Интервал (а,b) является открытым множеством, т.к. все точки внутренние, причем а,b – предельные точки. Отрезок [а,b] – замкнутое множество, т.к. содержит все предельные точки. Промежуток [а,b) не является открытым или замкнутым множеством.
Теорема 2. Если х предельная точка множества Х, то любая её 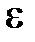 - окрестность содержит бесконечное число точек множества Х.
- окрестность содержит бесконечное число точек множества Х.
□ От противного. Предположим, что существует окрестность 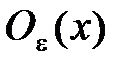 , которая содержит конечное число точек множества Х. Обозначим эти точки
, которая содержит конечное число точек множества Х. Обозначим эти точки 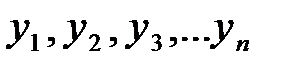 . Ясно, что
. Ясно, что 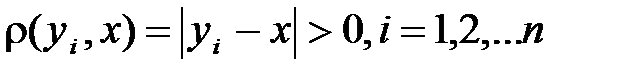 . Поэтому
. Поэтому 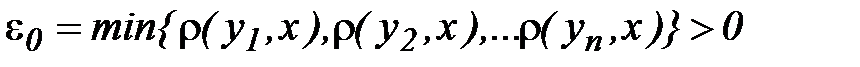 . Окрестность
. Окрестность 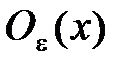 не содержит точек множества Х отличных от х, т.к.
не содержит точек множества Х отличных от х, т.к. 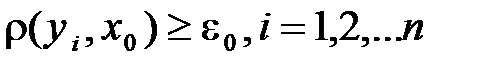 . Однако это невозможно, поскольку х – предельная точка множества Х. ■
. Однако это невозможно, поскольку х – предельная точка множества Х. ■
Комплексные числа
Обозначим через С – множество всех упорядоченных пар действительных чисел 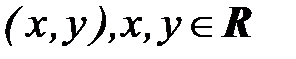 . Будем обозначать их
. Будем обозначать их 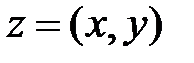 . Определим на этом множестве операции сложения и умножения.
. Определим на этом множестве операции сложения и умножения.
Суммой двух упорядоченных пар 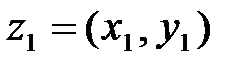 и
и 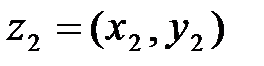 назовем упорядоченную пару
назовем упорядоченную пару 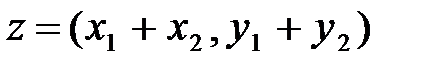 .
.
Произведением двух упорядоченных пар 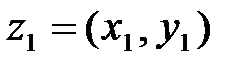 и
и 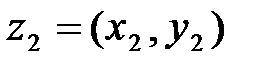 назовем упорядоченную пару
назовем упорядоченную пару 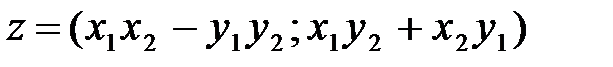 .
.
Две упорядоченные пары называются равными, если х1= х2, y1= y2.
Определение 23. Множество С упорядоченных пар z=(х, y), с введенными на нем операциями сложения или умножения, называется множеством комплексных чисел.
Рассмотрим частный случай, возьмем комплексные числа (х1, 0) и (х2, 0).
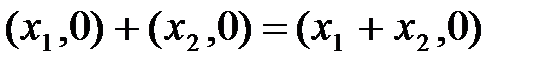 ;
;
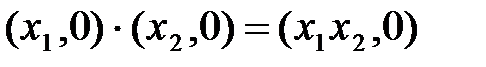 ;
;
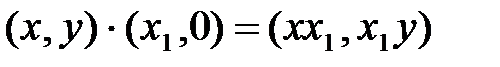 .
.
Таким образом, в результате сложения и умножения комплексных чисел (х, 0) получили комплексное число такого же вида , а при умножении на (х, y) получили пару, в которой каждый элемент умножается на х1. Поэтому комплексное число (х, 0) можно отождествить с вещественным числом х. Следовательно, множество R оказывается вложенным в множество комплексных чисел С.
Введем обозначение 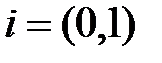 . Тогда получим, что
. Тогда получим, что
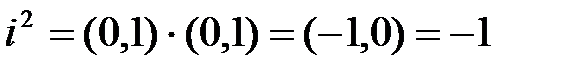 .
.
Число (1,0)=1 будем называть действительной единицей, а число (0,1)=i -мнимой единицей.
Тогда любое комплексное число можно записать в алгебраическом виде:
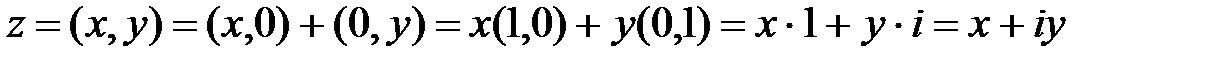 ,
, 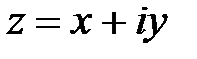 .
.
Число х называется действительной частью комплексного числа 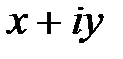 , а y – мнимой частью комплексного числа
, а y – мнимой частью комплексного числа 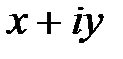 . Обозначается
. Обозначается 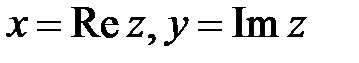 .
.
Сложение и умножение комплексных чисел обладают свойствами аналогичными свойствам действительных чисел. В частности:
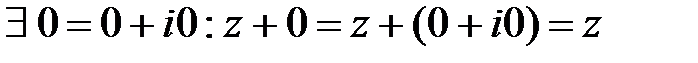 - существует нулевой элемент;
- существует нулевой элемент;
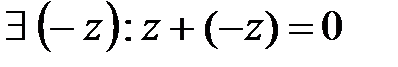 - существует противоположный элемент;
- существует противоположный элемент;
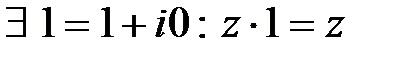 - существует единичный элемент;
- существует единичный элемент;
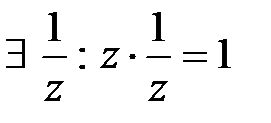 - существует обратный элемент, где
- существует обратный элемент, где 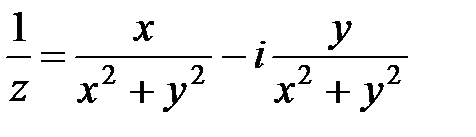 .
.
Поскольку, существуют нулевой и единичный элемент, то можно ввести операции вычитания и деления комплексных чисел.
Разностью комплексных чисел z1 и z2 называется комплексное число z такое, что 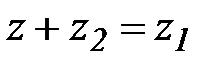 . Обозначение:
. Обозначение:
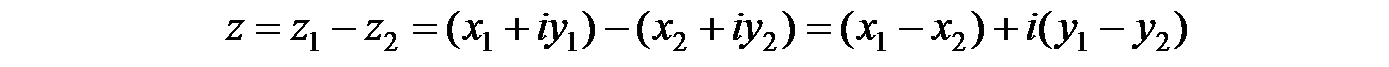 .
.
Частным от деления 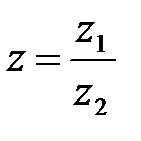 называется комплексное число z такое, что
называется комплексное число z такое, что 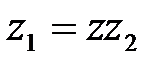 :
:
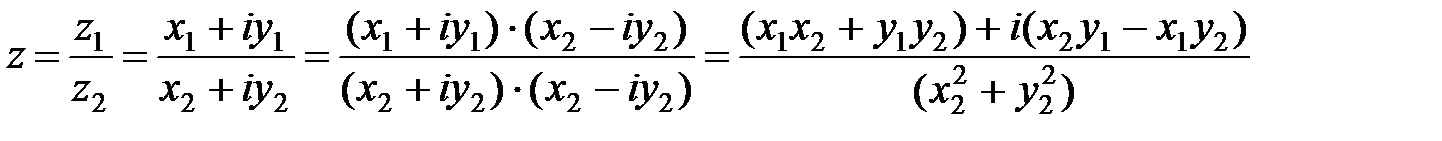 .
.
Замечание. Из определения комплексного числа в алгебраической форме и правил арифметических действий следует, что при действиях над комплексными числами можно пользоваться правилами действия с алгебраическими двучленами, учитывая, что i2=-1, 1/i=-i.
Комплексное число 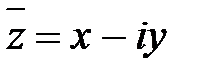 называется комплексным сопряженным с комплексным числом
называется комплексным сопряженным с комплексным числом 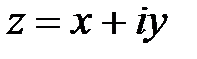 . Свойства сопряженных комплексных чисел:
. Свойства сопряженных комплексных чисел:
1) 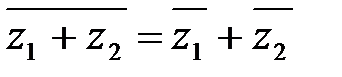 , 2)
, 2) 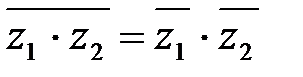 , 3)
, 3) 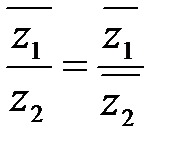 .
.
На множестве комплексных чисел можно решать квадратные уравнения с отрицательным дискриминантом. Например,
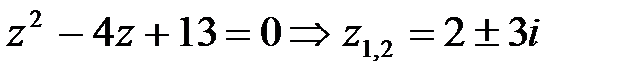 .
.
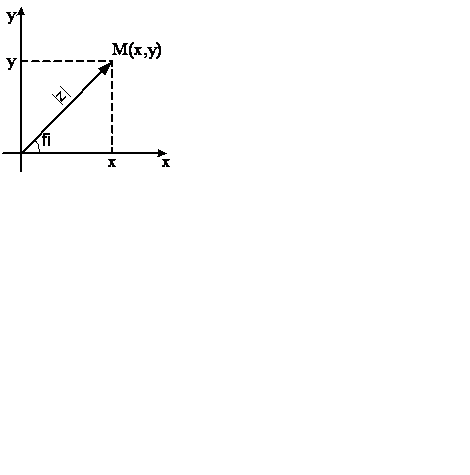
Геометрическая интерпретация комплексных чисел. Каждому комплексному числу z=х+iy на плоскости Oxy соответствует точка М(х,y) и каждой точке на плоскости будет соответствовать одно единственно число.
Число 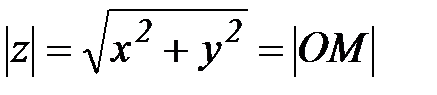 называется модулем комплексного числа z. Полярный угол φ между положительным направлением оси Ох и радиусом вектором ОМ называется аргументом комплексного числа z (
называется модулем комплексного числа z. Полярный угол φ между положительным направлением оси Ох и радиусом вектором ОМ называется аргументом комплексного числа z ( 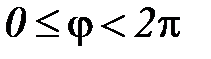 ).
).
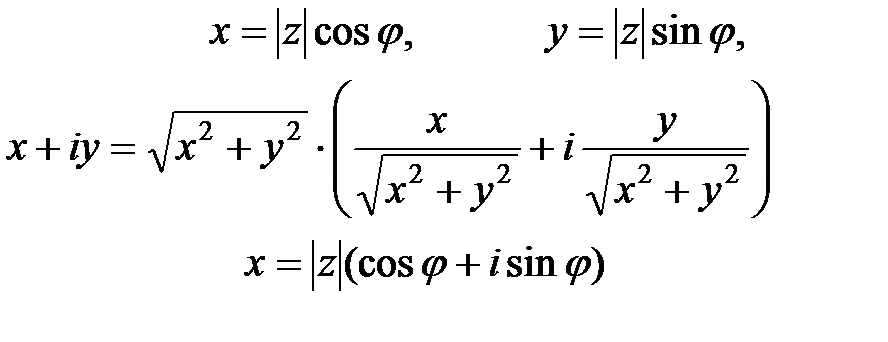
– эта формула называется тригонометрической формой комплексного числа.
Пусть 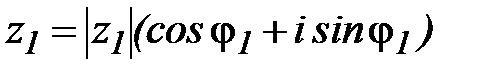 ,
, 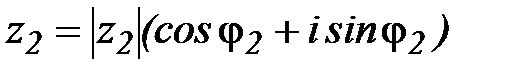 – два комплексных числа. Тогда, с помощью соответствующих тригонометрических формул и метода математической индукции легко показать, что справедливы следующие операции над комплексными числами в тригонометрической
– два комплексных числа. Тогда, с помощью соответствующих тригонометрических формул и метода математической индукции легко показать, что справедливы следующие операции над комплексными числами в тригонометрической
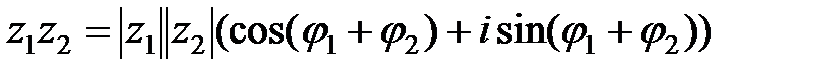 ,
,
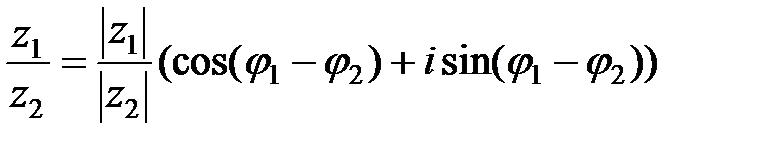 ,
,
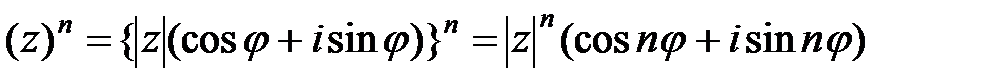 .
.
1.5. Контрольные вопросы
1.Приведите примеры различных множеств. Приведите пример совпадающих множеств.
2.Сколько можно образовать подмножеств из множества 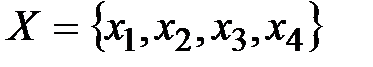 ?
?
3.Что называется декартовым произведением? Дайте определение отображения множества на множество.
4.Какие числа образуют множество вещественных чисел?
5.Перечислите основные свойства (аксиомы) вещественных чисел.
6.Каким основным свойством отличается множество всех вещественных чисел от множества только рациональных чисел?
7.Какие числовые множества называются промежутками?
8.Из отрезка 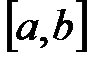 удален интервал
удален интервал 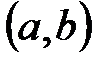 . Что осталось?
. Что осталось?
9.Из отрезка 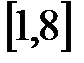 удален интервал
удален интервал 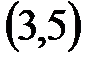 . Что осталось? Запишите множество оставшихся чисел с помощью промежутков.
. Что осталось? Запишите множество оставшихся чисел с помощью промежутков.
10.Дайте определение ограниченного сверху (снизу) множества X; приведите примеры.
11.Дайте определение точной верхней (нижней) грани ограниченного (снизу) множества 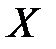 ; приведите примеры.
; приведите примеры.
12. Применяя правило построения отрицаний, сформулируйте определение неограниченного множества.
13. Привести пример множества, имеющего: а) ровно одну предельную точку; б) ровно шесть предельных точек.
14. Может ли множество, состоящее только из изолированных точек, иметь предельные точки?
15. Является ли замкнутым множеством множество рациональных точек отрезка [0,1]?
16. Привести пример множества, не являющимся ни замкнутым, ни открытым. Привести пример множества, являющегося одновременно открытым и замкнутым.
17.Что означает символическая запись: а) 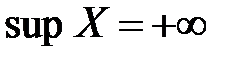 ; б)
; б) 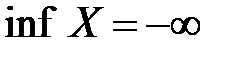 ?
?
18.Докажите равносильность неравенства 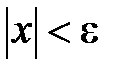 и
и 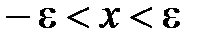 .
.
19. Что больше: 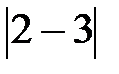 или
или 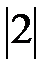 +
+ 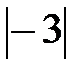 ?
?
20.Найдите 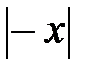 , если
, если 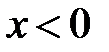 .
.  Верно ли, что
Верно ли, что 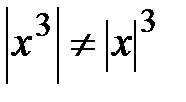 , если
, если 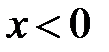 ?
?
21.Запишите без знака модуля выражение 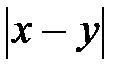 , если
, если 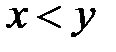 .
.
22.В чем состоит метод математической индукции?
23.Методом математической индукции докажите, что для любого натурального 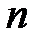 справедлива формула
справедлива формула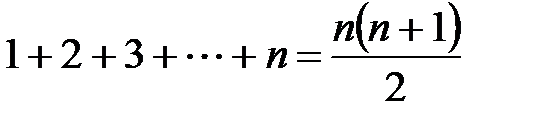 .
.
24.Что означает запись 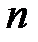 ! Найдите число
! Найдите число 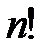 для
для 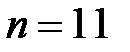 ;
; 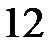 .
.
25. Может ли 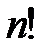 кончаться ровно пятью нулями?
кончаться ровно пятью нулями?
26.Запишите формулу бинома Ньютона.
