Указания к решению задач контрольной работы №6

К задаче 6.1

В корзине 4 яблока одного сорта и 5 яблок второго сорта. Наугад берут 2 яблока. Найти вероятность того, что взятые яблоки разных сортов.

Пусть событие А – взятые из корзины два яблока разных сортов.

Всего яблок в корзине 9, из них сочетаний по два , то есть число всех возможных исходов .

Событию А благоприятствуют пары, элементами которых являются яблоки разных сортов. Согласно принципу умножения количество таких пар равно

Используя классическое определение вероятности, получим искомую вероятность события А

К задаче 6.2

Устройство состоит из 10 блоков. Надежность каждого блока равна 0,8. Блоки могут выходить из строя независимо друг от друга. Найти вероятность того, что а) откажут два блока; б) откажет хотя бы один блок; откажут не меньше двух блоков.

Пусть событие А – отказ работы блока. Тогда вероятность события А по условию равна

, тогда

Согласно условию задачи . Используя формулу Бернулли

получим:

К задаче 6.3

Электростанция обслуживает сеть из 10000 ламп. Вероятность включения каждой из них 0,6. Найти вероятность одновременного включения от 5900 до 6100 ламп.

Для нахождения вероятности используем формулы интегральной теоремы Муавра-Лапласа:

где – интегральная функция Лапласа,

По формуле (2) имеем

Тогда по формуле (1) искомая вероятность равна

Значение интегральной функции Лапласа взято из Приложения 4 на с. 42 данного пособия и использовано свойство нечетности функции : .

К задаче 6.4

а) Непрерывная случайная величина X задана интегральной функцией распределения

Найдем дифференциальную функцию распределения :

Вероятность попадания случайной величины в интервал, например, равна

б) Непрерывная случайная величина X задана дифференциальной функцией распределения

Найдем значение параметра a из условия

то есть

отсюда .

Найдем интегральную функцию распределения

Если , то

Если , то

Таким образом,

Определим числовые характеристики случайной величины X по следующим формулам математического ожидания

и дисперсии

Вычислим математическое ожидание по формуле (3):

и дисперсию по формуле (4):

Построим графики интегральной функции распределения 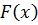(рис. 5) и дифференциальной функции распределения 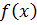(рис. 6):

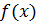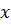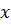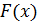Рис. 5

Рис. 6

Найдем вероятность того, что случайная величина 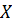попадет в интервал . Используем для этого формулу

в интервале ; вне этого интервала . Следовательно, искомая вероятность

К задаче 6.5

Данные наблюдений представлены в виде вариационного ряда (данные сгруппированы):

Объем выборки , число групп выборки . Находим выборочное среднее:

Аналогично найдем величину

Тогда выборочная дисперсия

а выборочное среднеквадратическое отклонение .

Считая, что исследуемый количественный признак является непрерывной нормально распределенной случайной величиной с неизвестными параметрам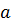и и 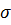, выпишем эмпирическую плотность его распределения с учетом найденных выборочных статистик

Здесь неизвестное математическое ожидание 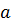заменено его точечной оценкой – выборочной средней, а среднеквадратическое отклонение 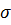– на выборочное среднеквадратическое отклонение . Получим эмпирическую плотность

По результатам выборочного исследования можно прогнозировать параметры генеральной совокупности как с помощью точечных оценок, так и методом интервального оценивания. Интервальная оценка определяется двумя числами – концами интервала, в котором с заданной наперед вероятностью (надежностью) окажется неизвестный параметр.

Найдем доверительный интервал для оценки математического ожидания 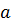с надежностью 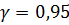. Если параметр 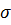неизвестен, то доверительный интервал будет следующий:

Подставим в это неравенство – выборочное среднее,
– выборочное среднее среднеквадратическое отклонение, 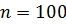– объем выборки. По уровню надежности 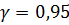и объему выборки 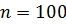найдем параметр из Приложения 5 на с. 43 данного пособия. Получим

Величина называется точностью оценки и характеризует ширину доверительного интервала. Итак, то есть неизвестное математическое ожидание 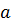заключено в доверительном интервале с надежностью 0,95. Полученный по данной выборке интервал покрывает неизвестный параметр 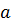с вероятностью 0,95.

К задаче 6.6

				–
	–

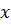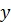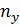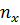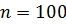Было произведено 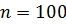измерений, в каждом из которых измерялись две величины 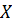и 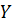. При большом числе измерений одно и то же значение 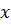может встретиться 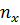раз, одно и то же значение 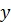– 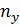раз, одна и та же пара чисел – раз. Поэтому данные наблюдений группируют, то есть подсчитывают частоты 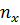, , 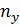. Сгруппированные данные записывают в виде так называемой корреляционной таблицы.

В первой строке таблицы указаны наблюдаемые значения переменной 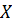, а в первом столбце – наблюдаемые значения переменной 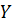. На пересечении строк и столбцов находятся частоты наблюдаемых пар значений переменных. Все частоты размещены в жирном прямоугольнике. Например, частота 12 указывает, что пара чисел наблюдалась 12 раз.

В последнем столбце записаны суммы частот строк. Например, сумма частот первой строки жирного прямоугольнике равна , то есть значение переменной 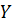, равное 10 (в сочетании с различными значениями переменной 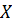), наблюдалось 15 раз.

В последней строк записаны суммы частот столбцов. Например, число 40 указывает, что значение переменной 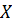, равное 5 (в сочетании с различными значениями переменной 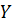), наблюдалось 40 раз.

В правой нижней клетке таблицы помещена сумма всех частот (общее число всех наблюдений). Очевидно, что .

В данном примере

, .

Составим корреляционную таблицу в условных переменных :

Выбрав (ложные нули), при , получим значения для переменной , – для переменной 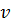. Корреляционная таблица в условных переменных примет вид:

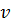	–2	–1
–1				–
	–

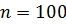Вычислим и :

Находим вспомогательные величины:

Находим выборочные среднеквадратические отклонения:

Коэффициент корреляции вычисляем по формуле

в которой все величины, кроме суммы, известны.

Для вычисления этой суммы составим расчетную таблицу:

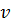	–2	–1
–1				–	–12
					–23
	–
	–2
		–2

В клетках последнего столбца записаны суммы произведений частот строки на соответствующие этим частотам значения переменной : . Например, число 12 получается суммированием произведений чисел в первой строке «жирного» прямоугольника на соответствующие значения переменной

Умножаем переменную 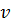на , и полученное произведение записываем в последнюю клетку той же строки, то есть в клетку столбца . Например, для первой строки , , следовательно, .

Сложив все числа столбца , получим сумму , которая равна искомой сумме .

Для контроля аналогичные вычисления выполняют по столбцам. Сложив все числа в последней строке , получим сумму которая при правильных вычислениях должна быть равна .

Искомая нами сумма:

Теперь вычисляем коэффициент корреляции:

Найдем остальные величины, входящие в уравнение регрессии:

В результате выборочное уравнение регрессии имеет вид

или окончательно

Приложения

Приложение 1. Основные правила дифференцирования

1. .

2. .

3. .

4.

Приложение 2. Основные формулы дифференцирования

Приложение 3. Основная таблица неопределенных интегралов

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

Приложение 4.Таблица значений функции

x	Ф(х)	x	Ф(х)	x	Ф(х)	x	Ф(х)	x	Ф(х)	x	Ф(х)
0,00	0,0000	0,45	0,1736	0,90	0,3159	1,35	0,4115	1,80	0,4641	2,50	0,4938
0,01	0,0040	0,46	0,1772	0,91	0,3186	1,36	0,4131	1,81	0,4649	2,52	0,4941
0,02	0,0080	0,47	0,1808	0,92	0,3212	1,37	0,4147	1,82	0,4656	2,54	0,4945
0,03	0,0120	0,48	0,1844	0,93	0,3238	1,38	0,4162	1,83	0,4664	2,56	0,4948
0,04	0,0160	0,49	0,1879	0,94	0,3264	1,39	0,4177	1,84	0,4671	2,58	0,4951
0,05	0,0199	0,50	0,1915	0,95	0,3289	1,40	0,4192	1,85	0,4678	2,60	0,4953
0,06	0,0239	0,51	0,1950	0,96	0,3315	1,41	0,4207	1,86	0,4686	2,62	0,4956
0,07	0,0279	0,52	0,1985	0,97	0,3340	1,42	0,4222	1,87	0,4693	2,64	0,4959
0,08	0,0319	0,53	0,2019	0,98	0,3365	1,43	0,4236	1,88	0,4699	2,66	0,4961
0,09	0,0359	0,54	0,2054	0,99	0,3389	1,44	0,4251	1,89	0,4706	2,68	0,4963
0,10	0,0398	0,55	0,2088	1,00	0,3413	1,45	0,4265	1,90	0,4713	2,70	0,4965
0,11	0,0438	0,56	0,2123	1,01	0,3438	1,46	0,4279	1,91	0,4719	2,72	0,4967
0,12	0,0478	0,57	0,2157	1,02	0,3461	1,47	0,4292	1,92	0,4726	2,74	0,4969
0,13	0,0517	0,58	0,2190	1,03	0,3485	1,48	0,4306	1,93	0,4732	2,76	0,4971
0,14	0,0557	0,59	0,2224	1,04	0,3508	1,49	0,4319	1,94	0,4738	2,78	0,4973
0,15	0,0596	0,60	0,2257	1,05	0,3531	1,50	0,4332	1,95	0,4744	2,80	0,4974
0,16	0,0636	0,61	0,2291	1,06	0,3554	1,51	0,4345	1,96	0,4750	2,82	0,4976
0,17	0,0675	0,62	0,2324	1,07	0,3577	1,52	0,4357	1,97	0,4756	2,84	0,4977
0,18	0,0714	0,63	0,2357	1,08	0,3599	1,53	0,4370	1,98	0,4761	2,86	0,4979
0,19	0,0753	0,64	0,2389	1,09	0,3621	1,54	0,4382	1,99	0,4767	2,88	0,4980
0,20	0,0793	0,65	0,2422	1,10	0,3643	1,55	0,4394	2,00	0,4772	2,90	0,4981
0,21	0,0832	0,66	0,2454	1,11	0,3665	1,56	0,4406	2,02	0,4783	2,92	0,4982
0,22	0,0871	0,67	0,2486	1,12	0,3686	1,57	0,4418	2,04	0,4793	2,94	0,4984
0,23	0,0910	0,68	0,2517	1,13	0,3708	1,58	0,4429	2,06	0,4803	2,96	0,4985
0,24	0,0948	0,69	0,2549	1,14	0,3729	1,59	0,4441	2,08	0,4812	2,98	0,4986
0,25	0,0987	0,70	0,2580	1,15	0,3749	1,60	0,4452	2,10	0,4821	3,00	0,49865
0,26	0,1026	0,71	0,2611	1,16	0,3770	1,61	0,4463	2,12	0,4830	3,20	0,49931
0,27	0,1064	0,72	0,2642	1,17	0,3790	1,62	0,4474	2,14	0,4838	3,40	0,49966
0,28	0,1103	0,73	0,2673	1,18	0,3810	1,63	0,4484	2,16	0,4846	3,60	0,499841
0,29	0,1141	0,74	0,2703	1,19	0,3830	1,64	0,4495	2,18	0,4854	3,80	0,499928
0,30	0,1179	0,75	0,2734	1,20	0,3849	1,65	0,4505	2,20	0,4861	4,00	0,499968
0,31	0,1217	0,76	0,2764	1,21	0,3869	1,66	0,4515	2,22	0,4868	4,50	0,499997
0,32	0,1255	0,77	0,2794	1,22	0,3883	1,67	0,4525	2,24	0,4875	5,00	0,499997
0,33	0,1293	0,78	0,2823	1,23	0,3907	1,68	0,4535	2,26	0,4881
0,34	0,1331	0,79	0,2852	1,24	0,3925	1,69	0,4545	2,28	0,4887
0,35	0,1368	0,80	0,2881	1,25	0,3944	1,70	0,4554	2,30	0,4893
0,36	0,1406	0,81	0,2910	1,26	0,3962	1,71	0,4564	2,32	0,4898
0,37	0,1443	0,82	0,2939	1,27	0,3980	1,72	0,4573	2,34	0,4904
0,38	0,1480	0,83	0,2967	1,28	0,3997	1,73	0,4582	2,36	0,4909
0,39	0,1517	0,84	0,2995	1,29	0,4015	1,74	0,4591	2,38	0,4913
0,40	0,1554	0,85	0,3023	1,30	0,4032	1,75	0,4599	2,40	0,4918
0,41	0,1591	0,86	0,3051	1,31	0,4049	1,76	0,4608	2,42	0,4922
0,42	0,1628	0,87	0,3078	1,32	0,4066	1,77	0,4616	2,44	0,4927
0,43	0,1664	0,88	0,3106	1,33	0,4082	1,78	0,4625	2,46	0,4931
0,44	0,1700	0,89	0,3133	1,34	0,4099	1,79	0,4633	2,48	0,4934

Приложение 5.Таблица значений

	0,95	0,99	0,999		0,95	0,99	0,999
	2,78	4,60	8,61		2,093	2,861	3,883
	2,57	4,03	6,86		2,064	2,797	3,745
	2,45	3,71	5,96		2,045	2,756	3,659
	2,37	3,50	5,41		2,032	2,720	3,600
	2,31	3,36	5,04		2,023	2,708	3,558
	2,26	3,25	4,78		2,016	2,692	3,527
	2,23	3,17	4,59		2,009	2,679	3,502
	2,20	3,11	4,44		2,001	2,662	3,464
	2,18	3,06	4,32		1,996	2,649	3,439
	2,16	3,01	4,22		1,991	2,640	3,418
	2,15	2,98	4,14		1,987	2,633	3,403
	2,13	2,95	4,07		1,984	2,627	3,392
	2,12	2,92	4,02		1,980	2,617	3,374
	2,11	2,90	3,97	∞	1,960	2,576	3,291
	2,10	2,88	3,92

Список литературы

Основная литература:

1. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. –М.: Наука, 2006.

2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: В 2 т. – М.: Высшая школа, 2008.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 2009.

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2009 г.

5. Гофман В.Г. Высшая математика. Курс лекций. – М.: МГТА, 2002 г.

Дополнительная литература:

6. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, ФМ, 1978 г.

7. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного: Учебник для втузов. – М.: Наука, 1989.

8. Кремер Н.Ш. Теория вероятностей и математическая статистика. – М.: ЮНИТИ, 2000.

9. Высшая математика. Методические указания и контрольные задания для студентов-заочников инженерных специальностей высших учебных заведений. Е.С. Мироненко. – М.: Высшая школа, 1998.

Для заметок

Трофимова Инна Викторовна

Математика

Рабочая программа, методические указания и

контрольные задания. Часть 2

Подписано к печати:

Тираж:

Заказ №: