Статистические методы обработки экспериментальных данных
Дисперсионный анализ. Основные понятия дисперсионного анализа. Однофакторный дисперсионный анализ.
Корреляционный анализ. Основные понятия корреляционного анализа. Точечные оценки двумерной корреляционной модели. Проверка значимости генерального коэффициента корреляции. Интервальная оценка генерального коэффициента корреляции.
Регрессионный анализ. Основные понятия регрессионного анализа. Планирование регрессионного эксперимента. Обработка результатов активного эксперимента методом регрессионного анализа.
Указания по выполнению контрольных работ
По дисциплине «Математика» студенты II курса заочной полной и сокращенной форм обучения должны выполнить две контрольные работы – №5 и №6. Контрольные работы выполняются по следующим разделам и темам рабочей программы:
№5 – математический анализ: двойные интегралы, ряды и дифференциальные уравнения;
№6 – теория вероятностей и математическая статистика.
Ниже приведены варианты заданий контрольных работ. Индивидуальный номер варианта соответствует последней цифре номера зачетной книжки. Последняя цифра «0» соответствует десятому варианту.
Студенты специальностей 0702, 1706 и 2713 задания 5.4 и 5.5 контрольной работы №5 не выполняют.
Контрольная работа №5
Задача 5.1.Изменить порядок интегрирования в двойном интеграле. Сделать чертеж области интегрирования.
1. 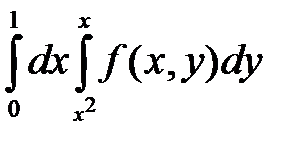 . 2.
. 2. 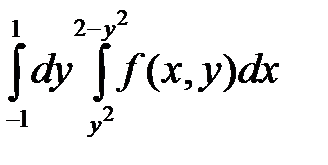 .
.
3. 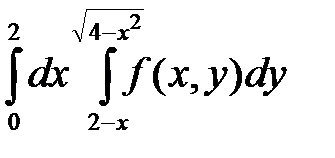 . 4.
. 4. 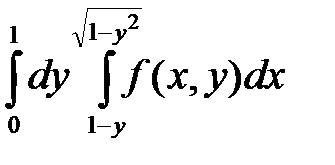 .
.
5. 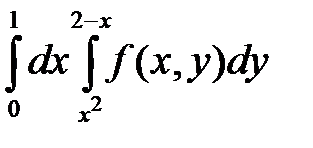 . 6.
. 6. 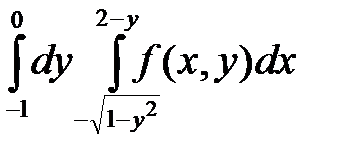 .
.
7. 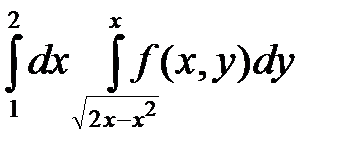 . 8.
. 8. 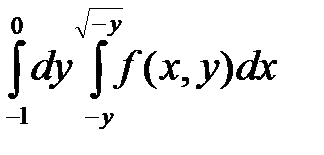 .
.
9. 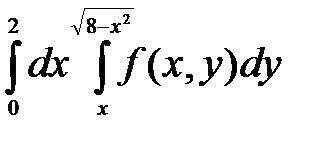 . 10.
. 10. 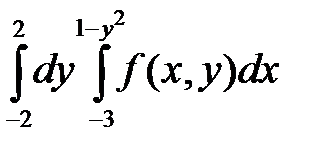 .
.
Задача 5.2.Вычислить объем тела, ограниченного указанными поверхностями. Сделать рисунок данного тела и его проекции на плоскость 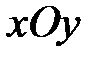 .
.
1. 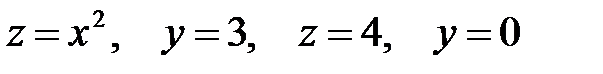 .
.
2. 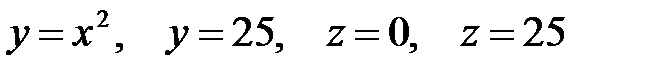 .
.
3. 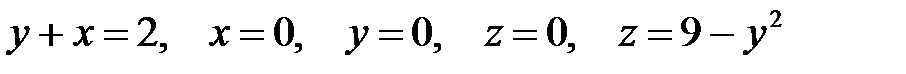 .
.
4. 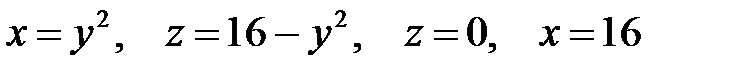 .
.
5. 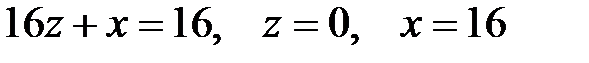 .
.
6. 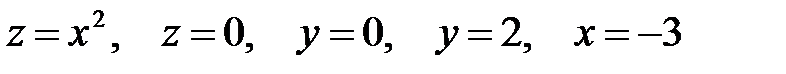 .
.
7. 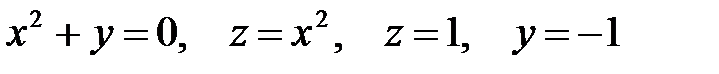 .
.
8. 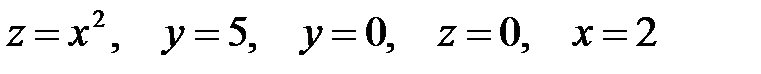 .
.
9. 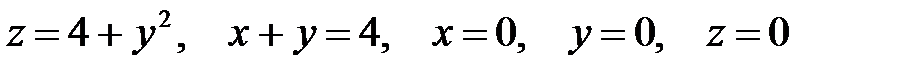 .
.
10. 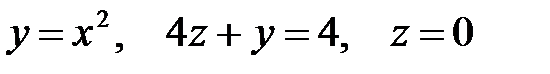 .
.
Задача 5.3.
В вариантах 1 – 4 найти координаты центра тяжести однородной фигуры, ограниченной линиями:
1. 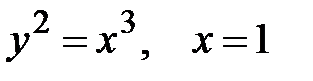 .
.
2. 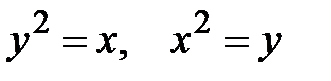 .
.
3. 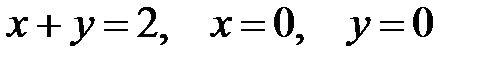 .
.
4. 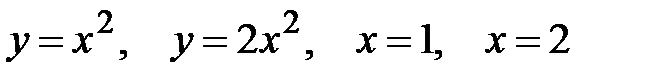 .
.
В вариантах 5 – 7 найти момент инерции относительно оси Oy однородной пластины, ограниченной линиями:
5. 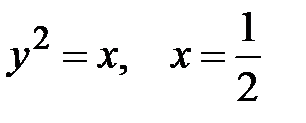 .
.
6. 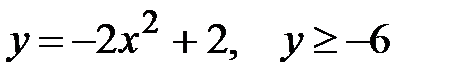 .
.
7. 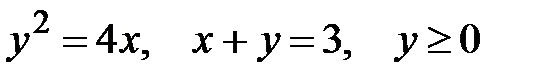 .
.
В вариантах 8 – 10 найти момент инерции относительно оси Ox однородной пластины, ограниченной линиями:
8. 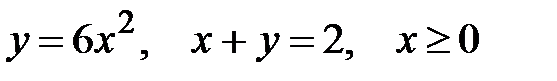 .
.
9. 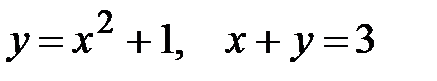 .
.
10. 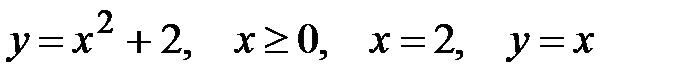 .
.
Задача 5.4.Исследовать на сходимость числовой ряд с помощью достаточных признаков сходимости.
1. а) 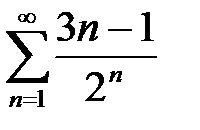 ; б)
; б) 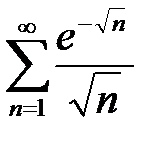 .
.
2. а) 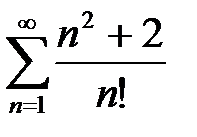 ; б)
; б) 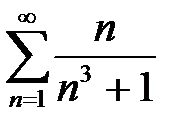 .
.
3. а) 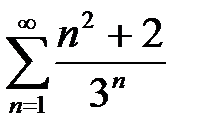 ; б)
; б) 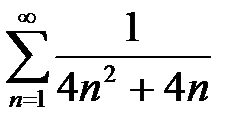 .
.
4. а) 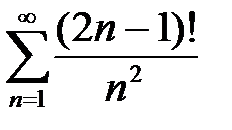 ; б)
; б) 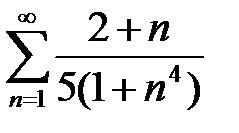 .
.
5. а) 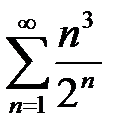 ; б)
; б) 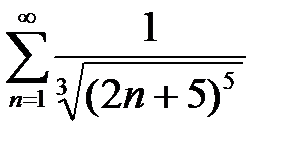 .
.
6. а) 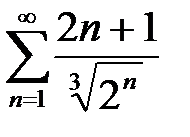 ; б)
; б) 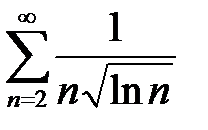 .
.
7. а) 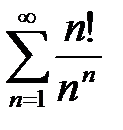 ; б)
; б) 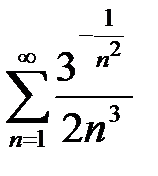 .
.
8. а) 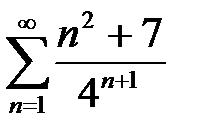 ; б)
; б) 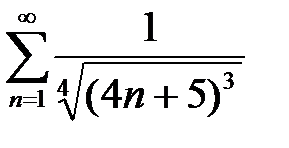 .
.
9. а) 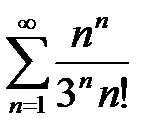 б)
б) 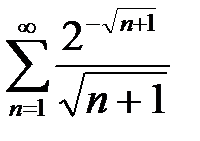 .
.
10. а) 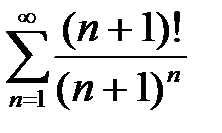 ; б)
; б) 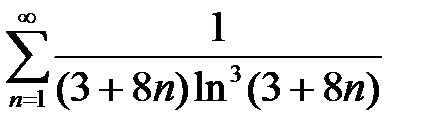 .
.
Задача 5.5.Найти область сходимости степенного ряда.
1. 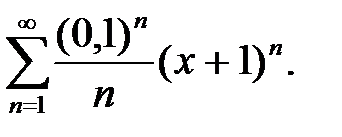 2.
2. 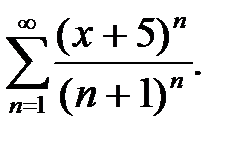
3. 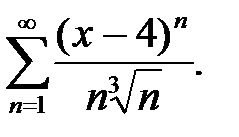 4.
4. 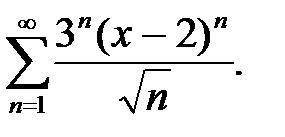
5. 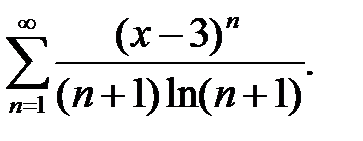 6.
6. 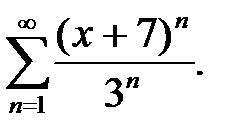
7. 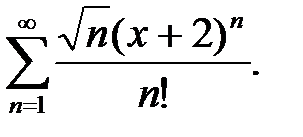 8.
8. 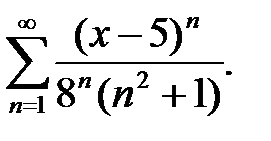
9. 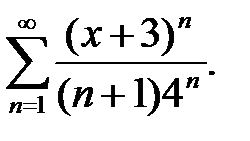 10.
10. 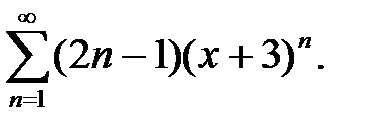
Задача 5.6.Найти частное решение дифференциального уравнения, удовлетворяющее начальному условию.
1. 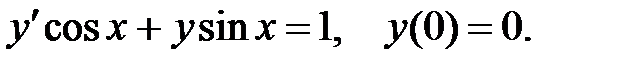
2. 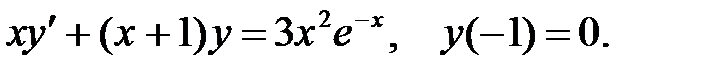
3. 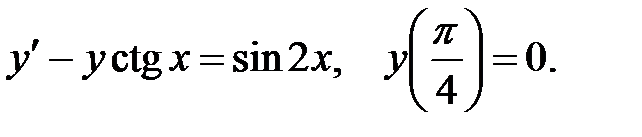
4. 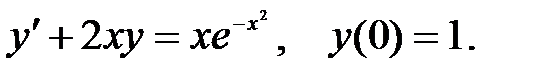
5. 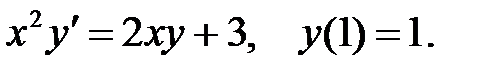
6. 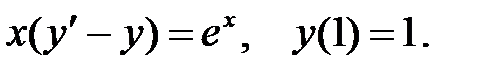
7. 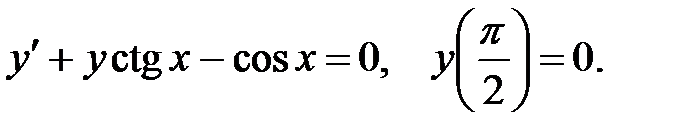
8. 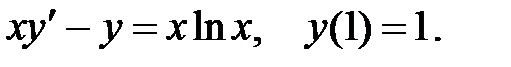
9. 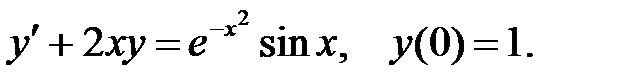
10. 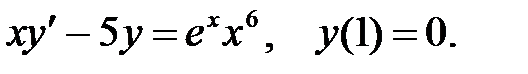
Задача 5.7.Найти общее решение дифференциального уравнения.
1. 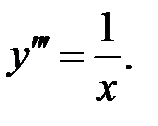 2.
2. 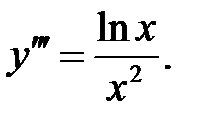
3. 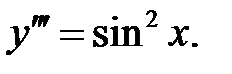 4.
4. 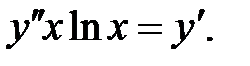
5. 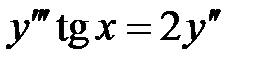 . 6.
. 6. 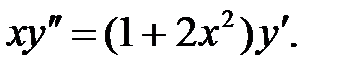
7. 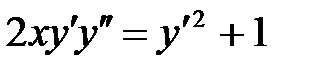 8.
8. 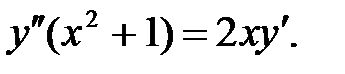
9. 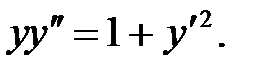 10.
10. 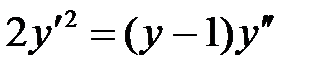 .
.
Задача 5.8.Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям.
1. 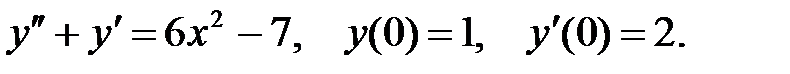
2. 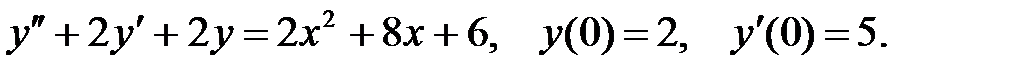
3. 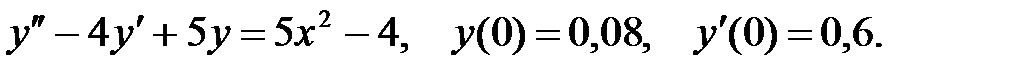
4. 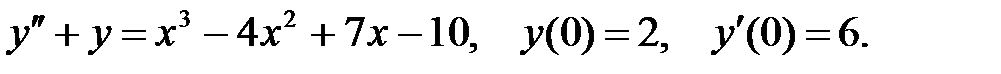
5. 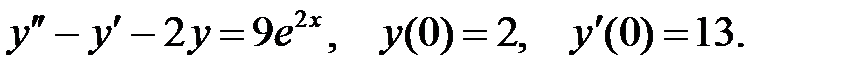
6. 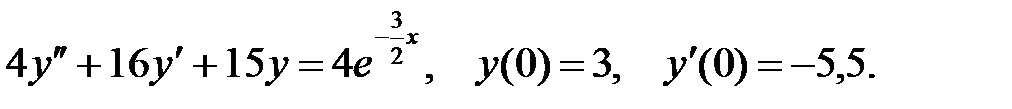
7. 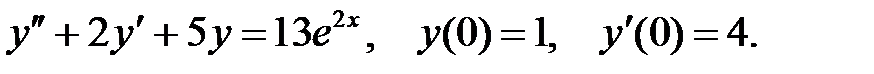
8. 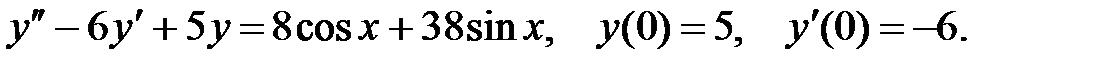
9. 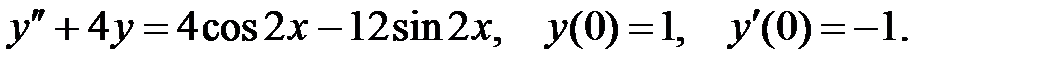
10. 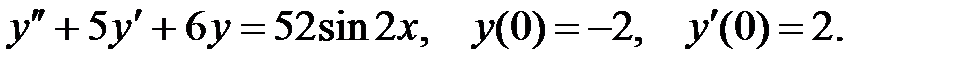
Указания к решению задач контрольной работы №5
К задаче 5.1
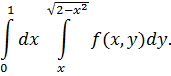
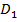 |
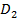 |
| x |
| y |
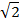 |
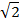 |
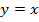 |
| Рис. 1 |
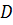 (рис.1) ограничена линиями
(рис.1) ограничена линиями 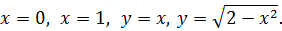
Найдем ординату точки пересечения двух последних линий:
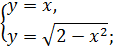
отсюда 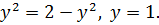
Изменим порядок интегрирования, для чего заданную область представим в виде двух областей 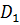 и
и 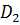 , где
, где
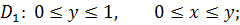
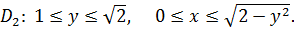
Следовательно,
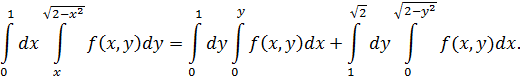
К задаче 5.2
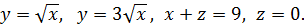
Заданное тело ограничено сверху плоскостью 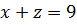 , снизу плоскостью
, снизу плоскостью 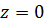 , с боков цилиндрами
, с боков цилиндрами 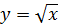 и
и 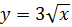 (рис. 2, 3).
(рис. 2, 3).
| x |
| y |
| z |
| y |
| x |
| D |
| Рис. 3 |
| Рис. 2 |
Следовательно,
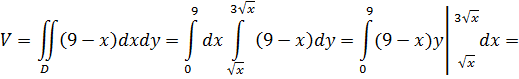
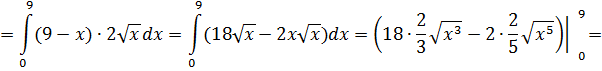
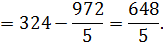
К задаче 5.3
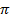 |
| x |
| y |
| Рис. 4 |
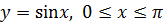 и осью Ox (плотность
и осью Ox (плотность 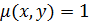 (рис. 4).
(рис. 4). Определим статические моменты 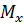 и
и 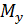 :
:
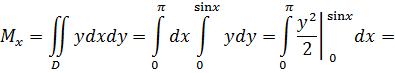
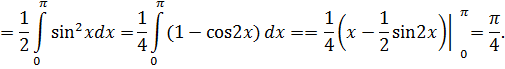
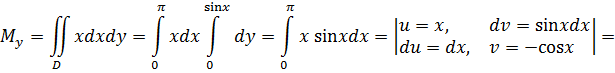
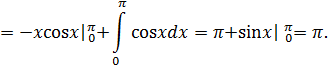
Определим площадь пластины:
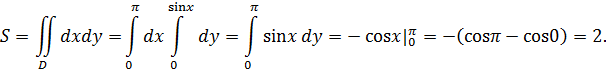
Находим координаты центра тяжести:
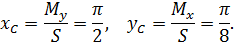
Определим момент инерции относительно оси Оy:
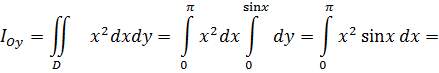
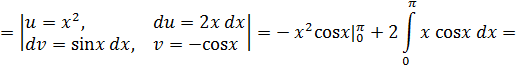
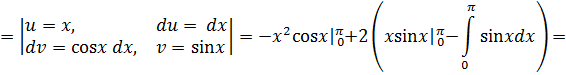
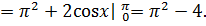
К задаче 5.4
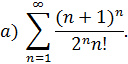
Используем признак Даламбера
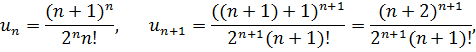
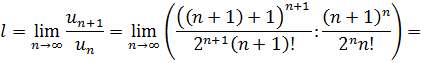
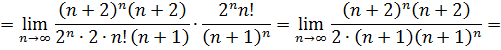
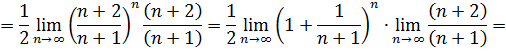
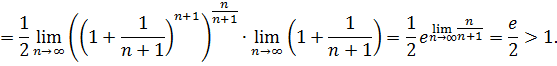
Получили 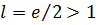 , значит, по признаку Даламбера данный ряд расходится.
, значит, по признаку Даламбера данный ряд расходится.
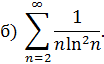
Так как функция 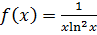 , составленная по общему члену ряда, непрерывная монотонно убывающая при
, составленная по общему члену ряда, непрерывная монотонно убывающая при 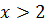 , то можем применить интегральный признак Коши:
, то можем применить интегральный признак Коши:
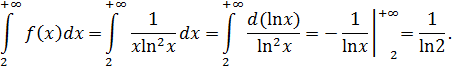
Так как несобственный интеграл сходится, то и ряд, к которому применили интегральный признак Коши, также сходится.
К задаче 5.5
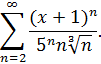
Найдем радиус сходимости данного ряда
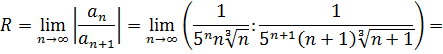
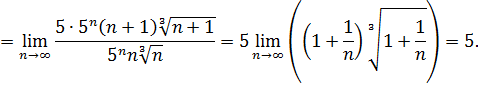
Ряд сходится абсолютно для всех 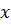 , удовлетворяющих неравенству
, удовлетворяющих неравенству
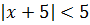 , то есть
, то есть 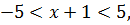
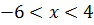 .
.
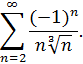 |
При 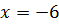 получаем числовой ряд
получаем числовой ряд
По признаку Лейбница этот ряд сходится, так как
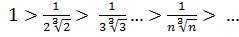
и
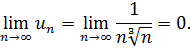
При 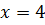 имеем числовой ряд
имеем числовой ряд
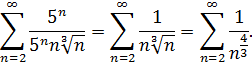
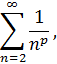 |

Этот ряд сходится как обобщенный гармонический ряд
где 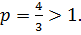
Значит, область сходимости данного ряда: 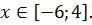
К задаче 5.6
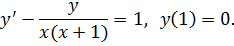
Это задача Коши для линейного обыкновенного дифференциального уравнения (ОДУ) первого порядка. Общее решение уравнения находим в виде 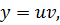 где
где 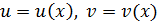 .
.
Подставим 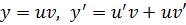 в данное ОДУ. Получим
в данное ОДУ. Получим
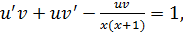
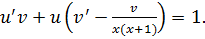
Ищем 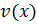 как частное решение ОДУ:
как частное решение ОДУ:
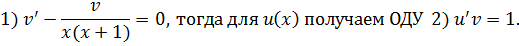
Оба уравнения с разделяющимися переменными. Решаем первое:
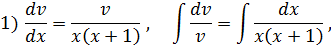
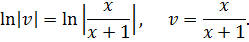
Подставляем 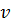 во второе уравнение:
во второе уравнение:
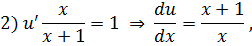
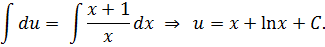
Тогда общее решение ОДУ принимает вид
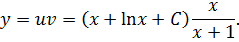
Используя начальное условие, имеем
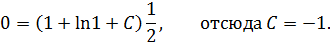
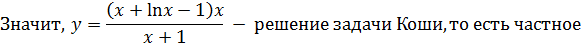
решение данного ОДУ, удовлетворяющее начальному условию.
К задаче 5.7
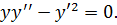
Это ОДУ второго порядка вида 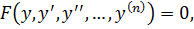 допускающее понижение порядка путем замены
допускающее понижение порядка путем замены
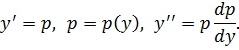
Подставляя эти выражения в данное ОДУ, получим уравнение с разделяющимися переменными
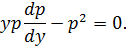
Полагая 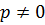 имеем
имеем
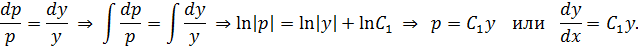
Разделим переменные в последнем уравнении и, проинтегрировав, получим общее решение данного уравнения
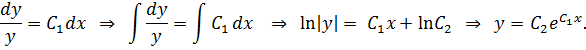
К задаче 5.8
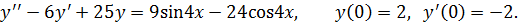
Имеем линейное неоднородное дифференциальное уравнение (ЛНДУ) второго порядка с постоянными коэффициентами.
Ищем общее решение в виде 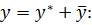
а) 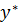 – общее решение однородного уравнения
– общее решение однородного уравнения 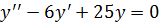 , его характеристическое уравнение
, его характеристическое уравнение 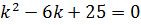 с корнями
с корнями 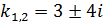 . Значит,
. Значит,
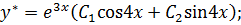
б) 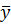 – частное решение данного ЛНДУ. Подберем его по виду правой части
– частное решение данного ЛНДУ. Подберем его по виду правой части 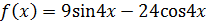 :
:
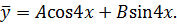
Найдем 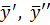 и подставим вместе с
и подставим вместе с 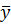 в данное уравнение:
в данное уравнение:
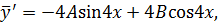
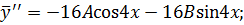
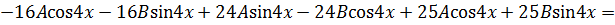
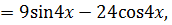
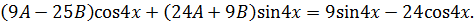
Приравнивая коэффициенты при 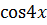 и
и 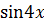 , получим систему уравнений
, получим систему уравнений
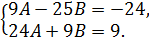
Решив систему, получим 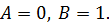
Таким образом, частное решение ЛНДУ имеет вид 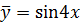 , а общее решение
, а общее решение
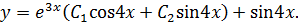
Отсюда
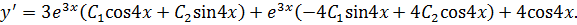
Подставив начальные условия 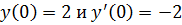 в формулы для
в формулы для 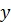 и
и 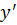 , получим систему уравнений
, получим систему уравнений
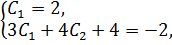
Отсюда 
Следовательно, 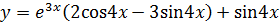 – решение задачи Коши, то есть частное решение данного ЛНДУ, удовлетворяющее начальным условиям.
– решение задачи Коши, то есть частное решение данного ЛНДУ, удовлетворяющее начальным условиям.
Контрольная работа №6
Задача 6.1.
1. При включении зажигания двигатель, независимо от остальных включений, начинает работать с вероятностью 0,7. Найти вероятность того, что:а) двигатель заработает при втором включении зажигания; б) для ввода двигателя в работу зажигание придется включать не менее четырех раз.
2. Человек забыл номер кода на дверном замке и помнит только, что этот код состоит их двух различных нечетных цифр. Какова вероятность того, что он с двух раз наберет код правильно?
3. В урне лежат 10 белых, 18 черных и 12 красных шаров. Случайным образом из урны вынимают два шара. Определить вероятность того, что вынутые шары окажутся разного цвета, если известно, что среди вынутых шаров нет белого.
4. На складе находится 8 костюмов 48-го размера, 12 костюмов 50-го размера и 10 костюмов 52-го размера. Случайным образом выбирают два костюма. Найти вероятность того, что они окажутся: а) одного размера; б) разных размеров.
5. В шахматном турнире участвуют 20 человек, которые по жребию разбиваются на две группы по 10 человек. Найти вероятность того, что двое наиболее сильных игроков попадут в разные группы.
6. На пяти карточках написаны буквы М, О, О, Р, Т. После тщательного перемешивания берут по одной карточке и кладут последовательно рядом: а) три карточки; б) пять карточек. Какова вероятность того, что получится слово: а) ТОР, б) МОТОР?
7. Три стрелка независимо друг от друга стреляют по мишени. Вероятность попадания в цель равна 0,7 для первого стрелка, 0,8 – для второго стрелка и 0,9 – для третьего стрелка. Найти вероятность того, что: а) все три стрелка попадут в цель; б) по крайней мере, два стрелка попадут в цель; в) только один стрелок попадет в цель.
8. Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на первый и второй вопросы одинакова и равна 0,9, на третий – 0,8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить: а) на все вопросы; б) по крайней мере, на два вопроса.
9. Два учебника по математике и три по физике произвольно расставлены на книжной полке. Какова вероятность того, что все учебники по одному предмету окажутся рядом?
10. Три предприятия заключают договор на поставку своей продукции. Вероятность выполнения договора первым предприятием равна 0,9, вторым – на 20% меньше, а третьим – 50 % от суммы двух первых вероятностей. Найти вероятность того, что договор выполнят: а) все три предприятия; б) только одно предприятие.
Задача 6.2.
1. Вероятность попадания стрелка в десятку равна 0,7, в девятку – 0,3. Чему равна вероятность того, что при трех выстрелах стрелок наберет не менее 29 очков.
2. Случайно встреченное лицо может оказаться с вероятностью 0,2 брюнетом, с вероятностью 0,3 – шатеном, с вероятностью 0,4 – блондином и с вероятностью 0,1 – рыжим. Найти вероятность того, что среди 5 встреченных лиц: а) не менее 3 блондинов; б) 2 шатена и 1 брюнет; в) хотя бы один рыжий.
3. Вероятность того, что семья имеет видеокамеру, равна 0,15. Какова вероятность того, что в десяти наугад выбранных семьях имеют видеокамеру: а) три семьи; б) не более трех.
4. Три элемента персонального компьютера работают независимо. Вероятность безотказной работы каждого элемента в течение времени t равна 0,8. Найти вероятность того, что на протяжении времени t: а) все элементы выйдут из строя; б) только два элемента работают безотказно; в) хотя бы один элемент будет работать исправно.
5. Какова вероятность того, что при 5 подбрасываниях монеты гербов выпадет больше, чем решек?
6. Вероятность того, что посетитель обувного магазина, сделает покупку, равна 0,4. Найти вероятность того, что из трех посетителей: а) только один приобретет обувь; б) ни один не сделает покупки; в) хотя бы двое посетителей приобретут обувь.
7. В люстре три лампы. Вероятность выхода из строя каждой лампы в течение года равна 0,2. Какова вероятность того, что в течение года придется заменить: а) две лампы; б) не более одной лампы; в) хотя бы одну лампу?
8. При установившемся технологическом процессе автомат производит 0,75 количества деталей 1-го сорта и 0,25 – 2-го сорта. Определить, что наиболее вероятно: получение трех первосортных деталей среди 5 наудачу отобранных или 4 первосортных среди 6 отобранных.
9. Игральный кубик подбрасывается 3 раза. Найти вероятность того, что четное число очков выпадет: а) два раза; б) ни разу; в) менее двух раз.
10. В семье пятеро детей. Найти вероятность того, что среди них: а) трое мальчиков; б) хотя бы один мальчик. Вероятности рождения мальчика и девочки считать одинаковыми.
Задача 6.3.
1. Найти вероятность того, что в результате 500 бросаний игральной кости выпадет 6 очков не менее 70 и не более 80 раз.
2. Партия изделий содержит 20% брака. Найти вероятность того, что среди 400 проверенных изделий попадется не менее 50 и не более 90 бракованных изделий.
3. Семена некоторого растения прорастают с вероятностью 0,8. Найти вероятность того, что из 2000 посаженных семян прорастет не менее 1600 семян.
4. Монету бросают 400 раз. Какова вероятность того, что герб при этом выпадет не менее 204, но не более 214 раз?
5. Саженец яблони приживается с вероятностью 0,8. Какова вероятность того, что из 400 саженцев приживутся более 250 саженцев?
6. Вероятность получить профессиональное заболевание для работников данного цеха равна 0,2. Найти вероятность того, что из 250 работников цеха заболеют не более 50 человек.
7. Среди 1100 студентов 1% – левши. Какова вероятность того, что из общего числа студентов не менее 20 левшей?
8. Игральный кубик подбрасывают 800 раз. Какова вероятность того, что число очков, кратное трем, выпадет не меньше 260 и не больше 274 раз?
9. Вероятность рождения мальчика равна 0,51. Найти вероятность того, среди 100 новорожденных окажется 50 мальчиков.
10. Вероятность правильной передачи бита равна 0,75. Найти вероятность того, что из последовательности, содержащей 100 информационных битов, число правильно переданных битов будет не меньше 71 и не больше 80.
Задача 6.4.
В задачах 1–5 непрерывная случайная величина 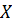 задана интегральной функцией распределения
задана интегральной функцией распределения 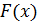 . Найти:
. Найти:
а) значение параметра a;
б) дифференциальную функцию распределения 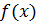 ;
;
в) математическое ожидание и дисперсию случайной величины 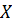 ;
;
г) построить графики функций 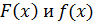 ;
;
д) вероятность того, что случайная величина попадет в интервал 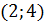 .
.
1. 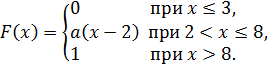
2. 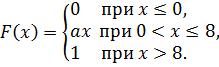
3. 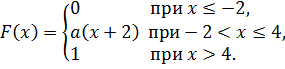
4. 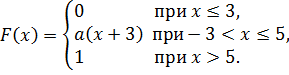
5. 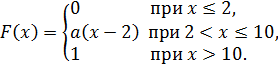
В задачах 6 – 10 непрерывная случайная величина 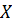 задана дифференциальной функцией распределения
задана дифференциальной функцией распределения 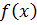 :
:
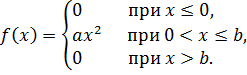
Найти:
а) значение параметра a;
б) интегральную функцию распределения 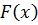 ;
;
в) математическое ожидание и дисперсию случайной величины 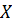 ;
;
г) построить графики функций 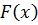 и
и 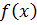 ;
;
д) вероятность того, что случайная величина 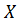 попадет в интервал
попадет в интервал 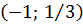 .
.
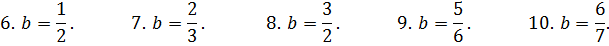
Задача 6.5.Найти выборочное среднее, выборочную дисперсию и выборочное среднеквадратическое отклонение по данным наблюдений. Считая, что исследуемый количественный признак является непрерывной нормально распределенной случайной величиной с неизвестными параметрами 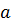 и
и 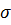 , выпишите эмпирическую плотность его распределения, найдите доверительный интервал для оценки математического ожидания
, выпишите эмпирическую плотность его распределения, найдите доверительный интервал для оценки математического ожидания 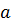 с надежностью
с надежностью 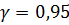 .
.
1. На ферме замеры жирности молока от различных коров, и результаты измерений представили в следующей таблице (  – содержание жира в пробах, %;
– содержание жира в пробах, %;  – количество проб с жирностью
– количество проб с жирностью 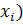 :
:
 | ||||||
 |
2. На заводе произвели замеры времени, необходимого для сборки одного узла разными рабочими результаты измерений представили в следующей таблице (  – время сборки, мин;
– время сборки, мин;  – число рабочих, собирающих узел за время
– число рабочих, собирающих узел за время  ):
):
 | |||||
 |
3. Лаборатория качества продукции исследовала на прочность несколько образцов кожи результаты исследований представила в следующей таблице (  – предельная нагрузка, выдерживаемая кожей, кг/мм2;
– предельная нагрузка, выдерживаемая кожей, кг/мм2;  – количество образцов, разрушившихся при нагрузке
– количество образцов, разрушившихся при нагрузке  ):
):
 | ||||||
 |
4. При изучении потребительского проса произведена выборка по размерам проданной мужской обуви, и результаты ее представлены в следующей таблице
(  – размер обуви;
– размер обуви;  – количество проданных пар размера
– количество проданных пар размера  ):
):
 | ||||||
 |
5. Данные о полученной прибыли от продажи произведенных кондитерских изделий за день представлены в следующей таблице (  – прибыль за день, у.е.;
– прибыль за день, у.е.;  – количество дней с прибылью
– количество дней с прибылью  ):
):
 | ||||||
 |
6. Данные об отклонении размера произведенного изделия от стандартного размера представлены в следующей таблице (  – отклонение, мм;
– отклонение, мм;  – количество изделий с отклонением
– количество изделий с отклонением  ):
):
 | 0,3 | 0,7 | 1,1 | 1,5 | 1,9 | 2,3 |
 |
7. Данные о росте 100 случайным образом отобранных юношей представлены в следующей таблице (  – рост, см;
– рост, см;  – число юношей роста
– число юношей роста  ):
):
 | ||||||
 |
8. Химическая лаборатория произвела анализ 50 проб воды из Москвы-реки на содержание солей тяжелых металлов, и результаты его представила в следующей таблице (  – содержание солей, мг/м3;
– содержание солей, мг/м3;  – число проб с содержанием солей
– число проб с содержанием солей  ):
):
 | 2,0 | 2,4 | 2,8 | 3,2 | 3,6 | 4,0 |
 |
9. Данные о размере изделий, изготавливаемых станком-автоматом, представлены следующей таблицей (  – размер изделия, см;
– размер изделия, см;  – количество изделий размера
– количество изделий размера  ):
):
 | |||||
 |
10. На сыродельном заводе взвесили 100 головок сыра одного сорта и результаты представили в следующей таблице (  – вес головки сыра, кг;
– вес головки сыра, кг;  – количество головок веса
– количество головок веса  ):
):
 | 1,3 | 1,5 | 1,7 | 1,9 | 2,1 |
 |
Задача 6.6.Найти выборочное уравнение линейной регрессии 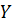 на
на 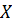 и коэффициент корреляции
и коэффициент корреляции 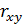 .
.
1.
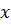 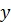 | 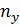 | ||||||
| – | – | – | – | ||||
| – | – | – | – | ||||
| – | – | – | |||||
| – | – | – | |||||
| – | – | – | |||||
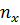 | 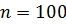 |
2.
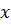 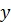 | 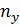 | ||||||
| – | – | – | – | ||||
| – | – | – | – | ||||
| – | – | – | |||||
| – | – | – | |||||
| – | – | – | |||||
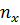 | 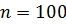 |
3.
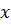 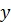 | 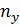 | ||||||
| – | – | – | – | ||||
| – | – | – | – | ||||
| – | – | – | |||||
| – | – | – | |||||
| – | – | – | |||||
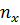 | 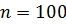 |
4.
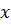 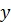 | 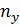 | ||||||
| – | – | – | – | ||||
| – | – | – | – | ||||
| – | – | – | |||||
| – | – | – | |||||
| – | – | – | |||||
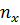 | 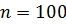 |
5.
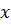 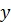 | 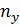 | ||||||
| – | – | – | – | ||||
| – | – | – | – | ||||
| – | – | – | |||||
| – | – | – | |||||
| – | – | – | |||||
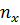 | Наши рекомендации
|
