Указания к решению задач контрольной работы №4
К задаче 4.1
Данная функция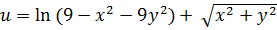 
определена и принимает действительные значения при 
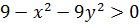и 
.
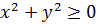Так как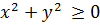 
для любых 
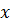и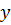 
, то областью определения 
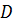данной функции является множество тех точек 
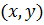, для которых .
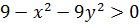Для изображения области 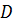найдем ее границу, поставив вместо знака неравенства знак равенства: 
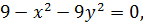или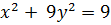 
, отсюда
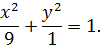
Это уравнение определяет в плоскости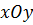 
эллипс с полуосям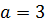и 
и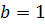 
. Эллипс делит всю плоскость на две части.
Чтобы проверить, какая из частей является областью определения данной функции, достаточно проверить условие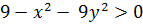 
для какой-либо одной точки, не лежащей на эллипсе. Например, точка 
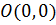принадлежит области 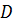, так как 
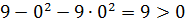. Следовательно, внутренними точками области 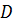данной функции являются точки, ограниченные эллипсом. Сам эллипс не принадлежит области 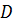(рис. 6).
| x |
| y |
| −3 |
| Рис. 6 |
| −1 |
К задаче 4.2
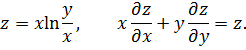
Находим частные производные:
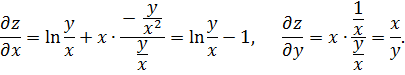
Подставляем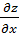 
и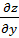 
в левую часть данного уравнения:
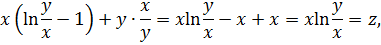
cледовательно, функция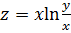 
действительно удовлетворяет данному уравнению.
К задаче 4.3
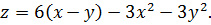
Находим частные производные первого порядка функции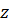 
:
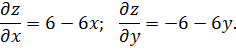
Для определения стационарных точек приравниваем к нулю эти производные:
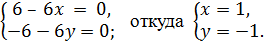
Таким образом, данная функция имеет только одну стационарную точку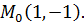 
Частные производные второго порядка данной функции постоянны:
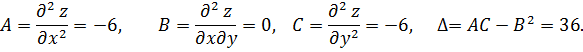
Поскольку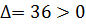 
и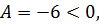 
то точка 
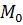есть точка максимума данной функции. При этом
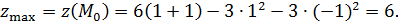
К задаче 4.4
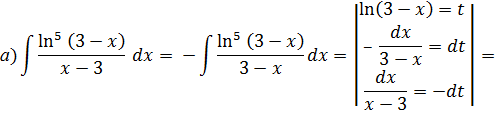
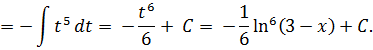
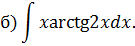
Используем формулу интегрирования по частям
.
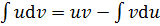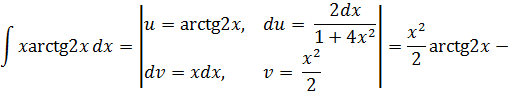
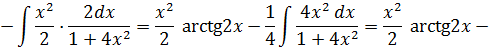
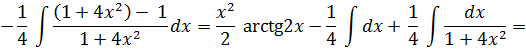
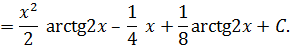
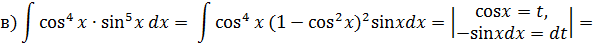
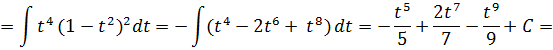
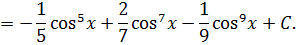
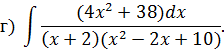
Разложим подынтегральную функцию на простейшие дроби:
g w:val="RU"/></w:rPr><m:t>+10</m:t></m:r></m:den></m:f><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="RU"/></w:rPr><m:t>, </m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">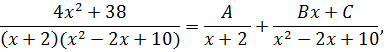 
отсюда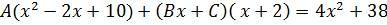 
.
При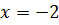 
получим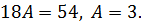 
Далее используем метод неопределенных коэффициентов. Составим систему уравнений для нахождения коэффициентов B и C:
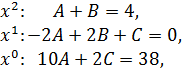отсюда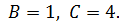 
Следовательно,
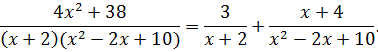
Имеем
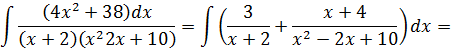
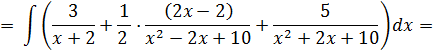
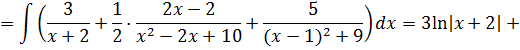
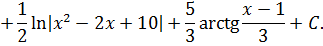
К задаче 4.5
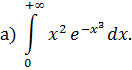
Применяя формулу Ньютона-Лейбница, получим:
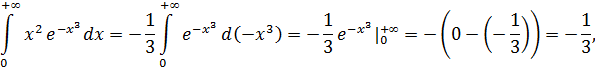
следовательно, интеграл сходится.
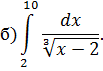
Функция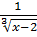 
непрерывна при 
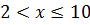и имеет бесконечный разрыв в точке 
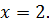Тогда
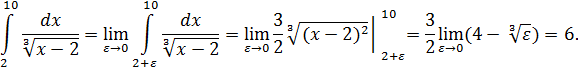
Интеграл сходится и равен 6.
К задаче 4.6
| Рис. 7 |
| x |
| y |
| −1 |
, 
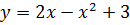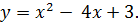
Находим абсциссы точек пересечения данных линий:
, 
, 
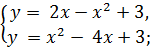
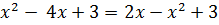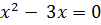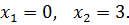
Это и есть пределы интегрирования.
По формуле
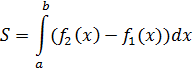
определяем площадь фигуры (рис. 7):
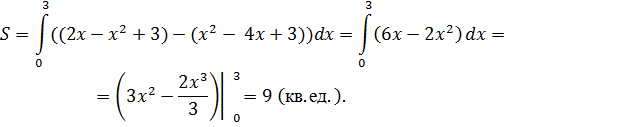
Приложения
Приложение 1. Основные правила дифференцирования
1. 
.
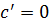2. 
.
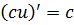3. 
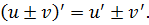
4. 
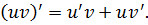
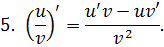
Приложение 2. Основные формулы дифференцирования
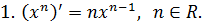
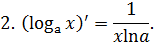
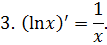
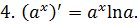
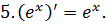
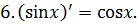
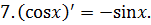
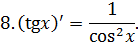
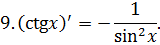
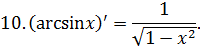
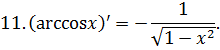
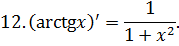
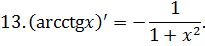
Приложение 3. Основная таблица неопределенных интегралов
1. 
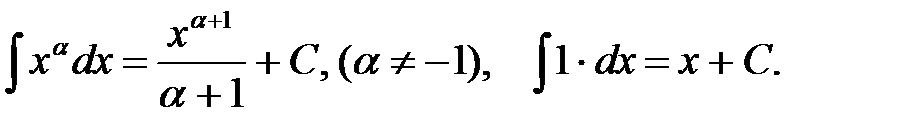
2. 
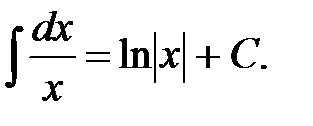
3. 
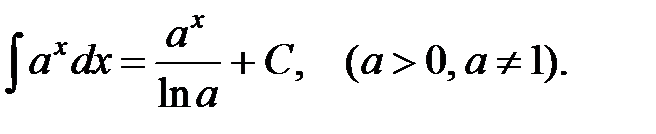
4. 
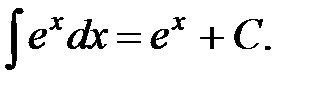
5. 
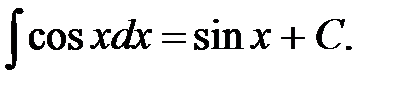
6. 
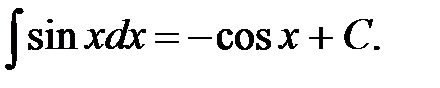
7. 
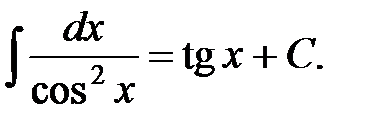
8. 
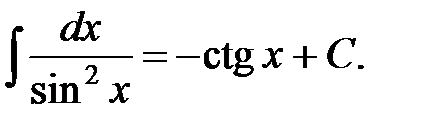
9. 
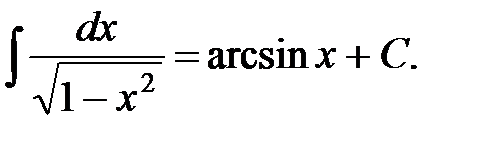
10. 
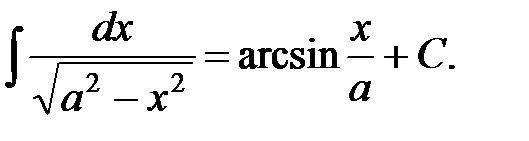
11. 
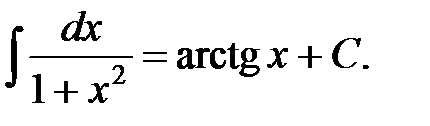
12. 
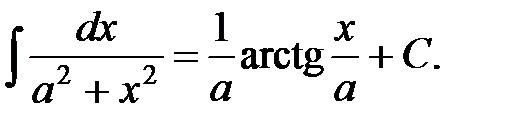
13. 
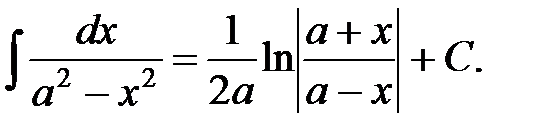
14. 
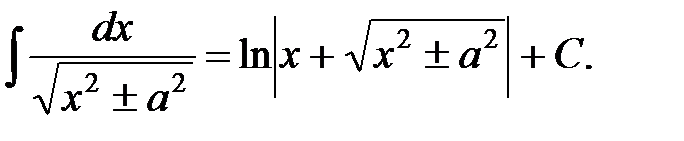
15. 
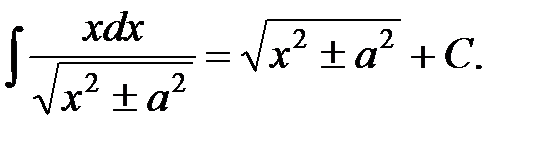
16. 
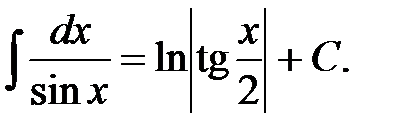
17. 
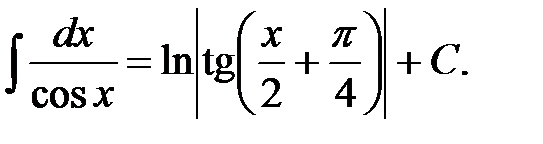
18. 
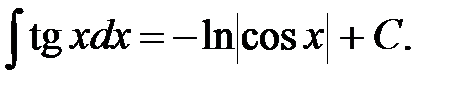
19. 
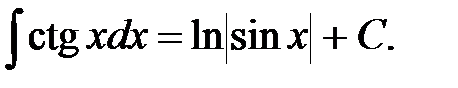
Список литературы
Основная литература:
1. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. –М.: Наука, 2006.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: В 2 т. – М.: Высшая школа, 2008.
3. Нефедов В.Н., Осипова В.А. Курс дискретной математики: Учеб. пособие. – М.: Изд-во МАИ, 1992.
4. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по курсу дискретной математики. – М.; «Наука», 2004.
5. Гофман В.Г. Высшая математика. Курс лекций. – М.: МГТА, 2002 г.
6. Зуев Ю.А. Лекции по дискретной математике. – М.: МГТА, 2007.
Дополнительная литература:
7. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, ФМ, 1978 г.
8. Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре: Учеб. пособие / Под ред. Д.В. Беклемишева. – М.: Наука, 1987.
9. Высшая математика. Методические указания и контрольные задания для студентов-заочников инженерных специальностей высших учебных заведений. Е.С. Мироненко. – М.: Высшая школа, 1998.
10. Шапорев С.Д. Дискретная математика. Курс лекций и практических занятий. – СПб: БВХ-Петербург, 2009.
11. Андерсон Д.А. Дискретная математика. – М.: «Вильямс», 2003.
12. Шевелев Ю.П.Дискретная математика. Учебное пособие. – СПб.: Издательство «Лань», 2008.
Для заметок
Трофимова Инна Викторовна
Математика
Рабочая программа, методические указания и
контрольные задания. Часть 1
Подписано к печати:
Тираж:
Заказ №: