Указания к решению задач контрольной работы №3
К задаче 3.1
Непосредственная подстановка в данное выражение предельного значения аргумента приводит к неопределенному выражению 
Следовательно, прежде чем перейти к пределу, преобразуем данное выражение
Имеем неопределенность вида Чтобы ее раскрыть, умножаем числитель и знаменатель на выражение, сопряженное числителю. После этого можно сократить на 
и применить свойство предела частного:
Имеем неопределенности вида 
которые можно раскрыть, поделив числитель и знаменатель дробей на 
, где k – старшая степень многочленов в числителе и знаменателе:
Имеем неопределенность вида 
. Преобразуем числитель и знаменатель по формулам тригонометрии и раскроем неопределенность, учитывая эквивалентность бесконечно малых:
Имеем неопределенности вида 
, которые раскрываем, используя второй замечательный предел:
1) Способ 1.
Способ 2. Воспользуемся формулой
К задаче 3.2
Функция определена при 
.
Чтобы функция была непрерывна в точке 
, необходимо, чтобы односторонние пределы при 
слева и справа были равны и равны значению функции в точке . Имеем
Следовательно, 
отсюда 
и 
График функции показан на рис. 4.
| x |
| y |
| −1 |
| Рис. 4 |
К задаче 3.3
а) 
.
1) Применим логарифмическое дифференцирование:
Итак,
> 
Дифференцируем заданное соотношение и определим затем 
:
г) 
Используем формулу производной параметрически заданной функции:
К задаче 3.4
Преобразуем функцию 
. При 
имеем неопределенность вида к которой применим правило Лопиталя дважды. Переходя к отношению производных, получим
К задаче 3.5
Исследование функции будем производить по следующей схеме:
1) находим область определения функции 
, точки разрыва;
2) находим асимптоты графика функции;
3) проверяем симметрию графика (четность, нечетность функции), периодичность;
4) находим интервалы монотонности, экстремумы;
5) находим интервалы выпуклости, вогнутости, точки перегиба;
6) находим точки пересечения с осями координат;
7) проводим, в случае необходимости, исследование графика на концах ;
8) строим график функции.
Исследуем данную функцию по изложенной выше схеме:
1) Область определения функции 
.
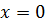– точка разрыва функции.
2) Вертикальная асимптота:
следовательно, 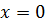– вертикальная асимптота.
Наклонная асимптота: 
.
следовательно, 
– горизонтальная асимптота.
4) Находим интервалы монотонности, экстремумы:
Для нахождения критических точек решаем уравнение 
, то есть
, отсюда 
– подозрительная на экстремум. Точка 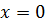– точка разрыва функции, она не может быть точкой экстремума. Составляем схему интервалов монотонности и экстремумов:
Знак  |
| Поведение функции y |
| −3 |
| + |
| − |
| − |
| x |
| max |
| точка разрыва |
Следовательно, 
На интервале 
функция возрастает, на интервале
функция убывает.
5) Находим интервалы выпуклости, вогнутости, точки перегиба:
при 
, 
, отсюда точка 
– подозрительная на перегиб. Точка 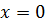– точка разрыва функции, она не может быть точкой пререгиба. Составляем схему интервалов выпуклости, вогнутости и точек перегиба:
Знак  |
| Поведение функции y |
| −4 |
| + |
| − |
| + |
| x |
| точка перегиба |
На интервале 
кривая вогнута, на интервале 
кривая выпукла. Точка – точка перегиба, f 
6) Находим точки пересечения с осью Ox:
Точек пересечения с осью Oy нет: 
.
7) Проводим дополнительное исследование:
а) на интервале 
, график функции выше оси Ox; на интервале 
, график функции ниже оси Ox.
б) исследуем поведение функции на бесконечности:
8) Строим график функции (рис. 5).
| −1 |
| −2 |
| −3 |
| −4 |
 |
| x |
| y |
| Рис. 5 |
Контрольная работа №4
Задача 4.1.Найти и построить область определения D данной функции.
1. 
. 2. 
.
3. 
. 4. 
.
5. 
. 6. 
.
7. 
. 8. 
.
9. 
. 10. 
.
Задача 4.2.Дана функция 
. Проверить, удовлетворяет ли эта функция заданному уравнению. Показать, что 
.
1. 
, 
.
2. 
, 
.
3. 
, 
.
4. 
, 
.
5. 
, 
.
6. 
, 
.
7. 
, 
.
8. 
, 
.
9. 
, 
.
10. 
, 
.
Задача 4.3.Исследовать на экстремум функцию.
1. 
.
2. 
.
3. 
.
4. 
.
5. 
.
6. 
.
7. 
.
8. 
.
9. 
.
10. 
.
Задача 4.4.Найти неопределенный интеграл.
1. а) 
; б) 
;
в) 
; г) 
.
2. а) 
; б) 
;
в) 
; г) 
.
3. а) 
; б) 
;
в) 
; г) 
.
4. а) 
; б) 
;
в) 
; г) 
.
5. а) 
; б) 
;
в) 
; г) 
.
6. а) 
; б) 
;
в) 
; г) 
.
7. а) 
; б) 
;
в) 
; г) 
.
8. а) 
; б) 
;
в) 
; г) 
.
9. а) 
; б) 
;
в) 
; г) 
.
10. а) 
; б) 
;
в) 
; г) 
.
Задача 4.5.Вычислить несобственные интегралы или установить их расходимость.
1. а) 
, б) 
.
2. а) 
, б) 
.
3. а) 
, б) 
.
4. а) 
, б) 
.
5. а) 
, б) 
.
6. а) 
, б) 
.
7. а) 
, б) 
.
8. а) 
, б) 
.
9. а) 
, б) 
.
10. а) 
, б) 
.
Задача 4.6.Вычислить площадь фигуры, ограниченной данными линиями.
1. 
2. 
3. 
4. 
.
5. 
6. 
7. 
8. 
9. 
10. 