Среднее квадратическое отклонение (стандарт)
Определение.Средним квадратическим отклонением (с.к.о.) случайной величины Х называется квадратный корень из её дисперсии:
. (12.6.1)
Среднее квадратическое отклонение имеет тот же смысл, что и дисперсия, т.е. является характеристикой рассеяния возможных значений случайной величины вокруг её математического ожидания. Вторая характеристика того же признака введена потому, что в отличие от дисперсии среднее квадратическое отклонение имеет ту же размерность, что и значения случайной величины. Например, если xiи МХ измеряются в метрах, то DX будет измеряться в квадратных метрах, что неудобно, а среднее квадратическое отклонение – соответственно снова в метрах.
Числовые характеристики основных дискретных распределений
Индикатор события
Найдём для характеристической случайной величины 
(8.2.1) её математическое ожидание, дисперсию и среднее квадратическое отклонение. Очевидно, что величина 
имеет такой же закон распределения, что и 
:
|
|
Тогда
(12.7.1)
Биномиальное распределение
Пусть случайная величина Х принимает значения k=0,1,2,…,п и распределена по биномиальному закону:
Р(Х=k)= 
(12.7.2)
Величину Х можно рассматривать как сумму независимых случайных величин
, (12.7.3)
где слагаемыми являются характеристические случайные величины. Действительно, рассмотрим индикаторы каждого из п испытаний
| c1 | c2 | ck | cn | |||||||||||
| p | q | р | p | q | р | p | q | р | p | q | р |
и составим ряд распределения случайной величины (12.7.3), которая по определению суммы случайных величин принимает возможные значения, равные всевозможным суммам, составленным из п нулей и единиц. Таких сумм будет 
, где k- число единиц в сумме. Вероятности принятия этих значений получим, перемножив вероятности р и q в нужных количествах.
Х=  | 0+0+…++0=0 (1 комбинация) | 0+0+…+ +0+1=1 (  комбинаций) | 0+0+…+0+ +1+1=2 (  комбинаций) | 0+0+…+ +1+1+…1=k (  комбинаций) | … … | 0+1+1+…+1= n-1 ( комбинаций) | 1+1+…+ +1=n (1 комбинация) |
| p | qn | 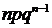 |  |  | …… | n  |  |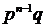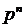
Получили биномиальное распределение случайной величины (12.7.3). Для нахождения её числовых характеристик воспользуемся свойствами линейности математического ожидания и дисперсии относительно суммирования и формулами (10.12.1):
(12.7.4)
Теперь становится понятным смысл случайной величины 
в приближённых формулах Лапласа (7.2.2, 7.2.4). А именно, Х представляет собой отклонение числа появлений события А от его математического ожидания (среднего значения), измеренное в стандартах, или так называемое нормированное отклонение.
Пример.Стрелок делает 2 выстрела в цель. Вероятность попадания при одном выстреле равна р, промаха – q. Тогда числа попаданий при первом и втором выстрелах имеют распределение
| c1 | c2 | |||||
| p | q | р | p | q | р |
Сумма 
имеет распределение
| | 0+1=1 | ||
| p | q2 | 2рq | p2 |
При трёх выстрелах имеем распределение:
 | ||||
| p | q3 | 3рq2 | 3pq2 | p3 |
Это частные случаи биномиального распределения при п=2 и 3.
Распределение Пуассона
Если случайная величина имеет распределение Пуассона (8.4.1), то она принимает значения k=0,1,2,… с вероятностями
(12.7.5)
В данном случае возможные значения случайной величины определяются бесконечной числовой последовательностью, и, следовательно, математическое ожидание выражается суммой бесконечного ряда
По сокращённой формуле (12.4.1) найдём дисперсию:
.
Здесь мы воспользовались тем, что выражение 
есть разложение экспоненты еl в ряд Маклорена. Таким образом, если случайная величина имеет распределение Пуассона, то и математическое ожидание, и дисперсия равны параметру l=пр, т.е. среднему числу появлений события А.