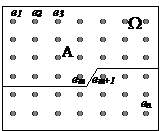По схеме равновозможных исходов

Как уже отмечалось, основным содержанием теории вероятностей как науки является определение вероятностей одних (более сложных) случайных событий по вероятностям других (более простых) исходных событий. Поэтому большое практическое значение имеют методы вычисления этих исходных вероятностей.

События называются равновозможными, если появление ни одного из них не является более предпочтительным (ожидаемым), чем появление любого другого. Для равновозможных исходов условия испытания обладают по отношению к ним известной симметрией. Последнее имеет место, например, при контроле качества массовой однородной продукции, проведении лотерей, жеребьевок, в азартных играх, и т.д.

Напомним, что исход называют благоприятствующим событию А, если событие А происходит при наступлении этого исхода. Событие А является множеством исходов, которые ему благоприятствуют: А={ 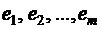}.. Например, при бросании игральной кости для события А – выпадения чётного числа очков – благоприятствующими являются исходы: { 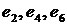}. Поэтому А={ }.

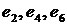Теорема. (Классическая формула для вычисления вероятности).

Пусть производится некоторое испытание и е₁, е₂, …,е_n – все элементарные исходы этого испытания. Пусть эти исходы равновозможны и пусть т исходов благоприятствуют событию А. Тогда вероятность события А можно вычислить по формуле:

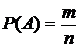, (4.3.1)

где n – число всех исходов, am – число исходов, благоприятствующих событию А.

Доказательство.

а) б)

е1	е2	е3
		ет	ет+1	ет+2
				еп

Рис.4.3.1

А=е₁+е₂+…+е_m

Вычислим вероятность события А. События е₁, е₂, …,е_n являются попарно несовместными, следовательно, по аксиоме 3

.

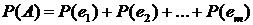Обозначим вероятность всех исходов буквой р (эти вероятности равны, т.к. исходы по условию равновозможны). Заметим, что вероятность р нам неизвестна. Тогда

Р(А)=mp (4.3.2)

С другой стороны, т.к. W= е₁+е₂+…+е_п,

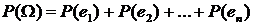, т.е.

1=np. (4.3.3)

Поделив (4.3.2) на (4.3.3), получим:

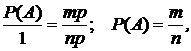
т.е. искомую формулу (4.3.1).

Формулу (4.3.1) называют также классическим определением вероятности, так называемый равновероятный случай.

Пример 1.В лотерее 1000 билетов, из них 150 выигрышных. Наугад вынимается 1 билет. Чему равна вероятность выигрыша?

n=1000; m=150; p=m/n=150/1000=0,15.

Пример 2.В урне 5 белых и 6 черных шаров. Наугад извлекается 1 шар. Какова вероятность того, что он белый?

n=5+6=11; m=5; p=5/11.

Пример 3.Монета бросается последовательно 3 раза. Найти вероятности выпадения ровно 0,1,2,3 гербов.

W={ггг, ггр, грг, грр, ргг, ргр, ррг, ррр}; n=8; m₀=1; m₁=3; m₂=3; m₃=1. Тогда

Р(0)=1/8; P(1)=3/8; P(2)=3/8; P(3)=1/8.

Задача о выборке

Пример 1. Испытание состоит в заполнении карточки спортлото 6 из 49. Найти вероятность того, что будет угадано ровно 4 номера.

Общее число исходов равно 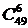. Исход является благоприятствующим, если 4 номера выбираются из 6 выигрышных номеров, а 2 оставшихся – из 43 невыигрышных (см. рис.4.4.1). По правилу умножения комбинаторики число благоприятствующих исходов

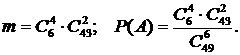
Рис.4.4.1. Выборка 4 из 6

Сформулируем задачу о выборке в общем виде.

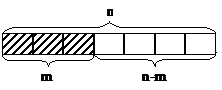
Пусть имеется N объектов, М из которых обладают некоторым признаком х. Наугад выбирается n объектов. Какова вероятность того, что среди них m объектов обладают признаком х?

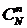Общее число элементарных исходов равно , т.к. мы можем выбрать комбинацию из п объектов 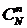способами. Событие А есть извлечение выборки из n объектов, из которых m обладают признаком х (см. рис.4.4.2). Исходом, благоприятствующим появлению события А, является появление группы из n объектов, в которой m объектов обладают признаком х, а n-m объектов - не обладают. Число таких групп по правилу умножения равно 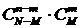, т.к. группу из m обладающих признаком х объектов можно образовать 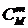способами, а группу из n-m остальных объектов выборки - 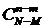способами. Тогда искомая вероятность события А находится по классической схеме:

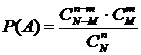. (4.4.1)

Рис.4.4.2

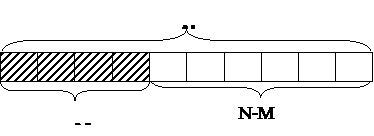
Рис.4.4.3

Пример 2.Из 10 деталей 4 бракованные. Наугад выбираются 7 деталей. Какова вероятность того, что среди них бракованных: 1) три; 2) ни одной; 3) четыре; 4) одна.

В формуле (4.4.1) 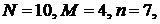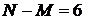, т различно для каждого вопроса задачи.

1) ;

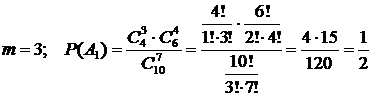2) качественных деталей всего 6, поэтому в выборке не может быть 7 качественных деталей .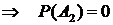

3) .

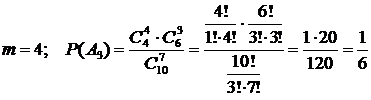4) .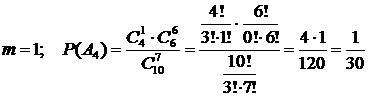