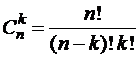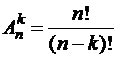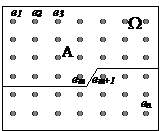История развития теории вероятностей.

ВВЕДЕНИЕ

История развития теории вероятностей.

Предмет теории вероятностей

Вероятность – это важнейшее понятие в современной науке особенно потому, что никто совершенно не представляет, что оно означает.

Бертран Рассел.

Первые задачи по вычислению вероятностей появились в XVII веке в работах французов Блеза Паскаля (1623-1662) и Пьера Ферма (Fermat, 1601-1665), швейцарца Якоба Бернулли (Bernoulli, 1654-1705), голландца Христиана Гюйгенса (Huygens, 1629-1695) и др. в связи с азартными играми (карты, кости, и т.д.). В XVIII и в начале XIX вв. в работах англичанина Абрахама де Муавра (1667-1754), датчанина А.К.Эрманга (1878-1929), французских ученых Пьера Симона Лапласа (Laplace, 1749-1827), Симеона Дениса Пуассона (Poisson, 1781-1840), Жоржа Бюффона (Buffon, 1707-1788) и др. появились первые результаты, связанные в основном с биномиальным распределением. Однако к этому времени не были еще чётко разработаны основные методы теории вероятностей, поэтому попытку некоторых учёных применять теоретико-вероятностные методы в прикладных задачах иногда приводили к результатам, не соответствующим реальным фактам. Это привело к тому, что к середине XIX века теория вероятностей стала непопулярной среди математиков. И лишь в России в начале ХХ века в трудах русских ученых Петербургского университета П.Л.Чебышева, А.М.Ляпунова, А.А.Маркова эта наука получила дальнейшее развитие.

Теория вероятностей – это наука о вычислении вероятностей случайных событий. Первоначально в ней изучались лишь стационарные явления. Необходимость исследования изменения процессов во времени послужила толчком к развитию теории вероятностей, а также к развитию, а иногда и появлению новых отраслей науки, таких, как квантовая механика, теория случайных процессов, теория надёжности, теория массового обслуживания, теория игр и др.

После введения советским ученым А.Н.Колмогоровым в 1933 г. аксиоматики теория вероятностей стала полноправной математической наукой, имеющей многочисленные применения в естественных науках (физике, биологии), технике, социологии, криптографии (науке о шифрах), военном деле и т.п. Например, в криптографии применяется метод стойкого шифрования (в отличие от слабого) с помощью случайных чисел. Если противнику не известен ключ, то перехваченный им шифр не может быть прочитан.

Однако даже в середине ХХ века бывали случаи, когда математикам приходилось защищать теорию вероятностей от обвинений в ненаучности некоторых её приложений. Например, в 30-40-е годы, в период гонений в нашей стране на генетику, многие законы которой обосновывались с помощью теории вероятностей, в газетах и псевдонаучных статьях появились высказывания типа «случайность – враг науки» и «природа не играет в кости». Русский ученый А.Я.Хинчин, обогативший теорию вероятностей целым рядом выдающихся результатов, сказал: «Да, это верно,- случайность – враг науки, но врага надо изучать, а это делает теория вероятностей».

Элементы комбинаторики.

Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов. Комбинаторика возникла в XVI веке, т.е. раньше теории вероятностей. В жизни привилегированных слоев общества большое место занимали азартные игры. Одним из первых занялся подсчётом числа различных комбинаций в игре в кости итальянский математик Никколо Тарталья (Tartaglia, ок. 1500-1557). Теоретическое исследование вопросов комбинаторики предприняли в XVII веке ученые Б.Паскаль и П.Ферма. Развитие комбинаторики связано с именами Якоба Бернулли, Готфрида Вильгельма Лейбница (Leibniz, 1646-1716) и Леонарда Эйлера (Euler, 1707-1783).

В последние годы комбинаторика переживает период бурного развития, связанного с повышением интереса к проблемам дискретной математики. Комбинаторные методы используются для решения транспортных задач, в частности задач по составлению расписаний, для составления планов производства и реализации продукции. Комбинаторика используется при решении задач линейного программирования, статистики, теории групп, геометрии, криптографии. Применяется также химиками при изучении расположения молекул, конструкторами, агрономами, биологами, и т.д.

Рассмотрим объекты (элементы) любой природы. Например, будем вынимать шары из урны, как это принято в теории вероятностей. Пусть в урне находится m белых и n чёрных шаров. Рассмотрим задачу о том, сколькими способами можно получить ту или иную комбинацию шаров. Под комбинацией будем понимать множество (последовательность) объектов, например, комбинацию из одного шара А- сам шар: {A}; комбинация из двух шаров - пара шаров, расположенных один за другим: {A, B}; из трёх шаров: {A, B, C}, и т.д. Если каждому объекту множества присвоен порядковый номер, то такое множество называется упорядоченным. Упорядоченные множества обычно обозначаются как последовательность элементов в круглых скобках, например, (А, В). Из неупорядоченного множества {A, B} можно получить две упорядоченные пары: (А, В) и (В, А). Например, из неупорядоченной пары {ч,б} (чёрный шар, белый шар) можно получить (ч,б) и (б,ч). Множество из трех объектов {A, B, C} (неупорядоченная тройка) можно упорядочить шестью способами: (А, В, С), (А, С, В), (В, А, С), (В, С, А), (С, А, В), (С, В, А) (упорядоченные тройки).

Задача 1. Сколькими способами можно вынуть один какой-либо шар (белый или чёрный) из урны?

Очевидно, что белый шар можно вынуть m способами, а чёрный – n способами. Тогда всего будет m+n способов. Об этом же говорит и принятое в комбинаторике

Правило суммы (правило сложения). Если объект А можно выбрать m способами, а объект В – n способами, то осуществить выбор объекта А или В можно m+nспособами.

Т.к. других шаров в урне нет, то m+n – это общее количество шаров в урне. Если же в урне имеются шары другого цвета, например, красные, то m+n не равно общему количеству шаров в урне.

Задача 2.Сколькими способами можно получить неупорядоченную пару «белый шар – чёрный шар»?

Будем рассуждать так: белый шар можно выбрать m способами, а к каждому из выбранных белых шаров можно взять в пару каждый из чёрных шаров. Следовательно, можно предположить, что число возможных пар равноm´n. В комбинаторике об этом гласит

Правило произведения (правило умножения).Если объект А можно выбрать m способами, а объект В – (после этого выбора) n способами, то выбор пары (А, В) можно осуществить m´n способами.

Можно сначала выбрать чёрный шар п способами, а к немубелый шар т способами.

Пример 1.Сколькими способами можно получить пару: два белых шара?

Первый шар можно выбрать т способами, второй -т–1 способами. По правилу произведения пару из двух белых шаров получим способами.

Пример 2.На главные роли в фильме пробуются 4 актера М₁, М₂, М₃ и М₄ и 2 актрисы W₁ и W₂. При этом известно, что M₁ и W₂ не подходят друг к другу по росту, а M₄ и W₁ психологически несовместимы. Сколько имеется вариантов состава исполнителей?

Ответ: 4´2–2=6.

(Всего пар 4х2, но 2 не годятся).

Замечание. Правила суммы и произведения можно распространить на любое число объектов (а не только для двух – А и В). В этом случае речь будет идти уже не о паре (А, В), а о некоторой комбинации (последовательности) большего числа элементов (A, B, C,…, Z).

Перестановки

Перестановками из n элементов называются комбинации из n элементов, которые отличаются друг от друга порядком расположения элементов. Иначе: Перестановки – это упорядоченные множества из п элементов. Число перестановок из п элементов обозначается Р_п.

Формула для определения числа всех перестановок:

(1.1.1)

Доказательство. Первый элемент можно выбрать n способами, 2-й – (n–1) способами, 3-й – (n–2) способами, последний - только одним способом. По правилу произведения

ч.т.д.

Пример 1.Сколькими способами можно расставить 5 судов у причальной стенки?

Пример 2.Сколькими способами можно рассадить 50 студентов по 50 местам аудитории?

Пример 3.Сколькими способами можно расставить 8 ладей на шахматном поле, чтобы они не били друг друга?

Перестановки с повторениями

Пусть некоторые из элементов повторяются (например, одинаковые буквы или цифры). Тогда внутри перестановки они могут образовывать свои перестановки, т.к. порядок одинаковых элементов не влияет на порядок внутри основной комбинации. Число перестановок основной комбинации будет уменьшаться во столько раз, каково значение каждой такой «малой» перестановки. Пусть, например, элемент А встречается k раз, элемент В – l раз,…, элемент Z – r раз. Тогда общее число перестановок с повторяющимися элементами

Замечание.Перестановки без повторений можно рассматривать как частный случай перестановок с повторениями. Рассмотрим множество А из п элементов , где i-й элемент ( ) повторяется раз, причем некоторые из могут быть равны 1. Тогда число перестановок с повторениями равно

Если все элементы встречаются в множестве А по одному разу, то получим формулу (1.1.1).

Пример 4. Сколько можно написать 7-значных чисел из цифр 1,1,2,2,2,3,3?

Если цифры не повторяются, то

Размещения

Размещениями из п элементов по 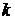элементов называются комбинации из 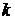элементов, которые отличаются друг от друга составом элементов и/или порядком их расположения. Иными словами, размещения - это упорядоченные подмножества из к элементов, выбранные из п-элементного множества. Число размещений обозначается (а из эн по ка).

Название «размещение» произошло от задачи: разместить 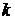предметов в п пронумерованных ячейках. Сколько последовательностей заполненных ячеек можно получить? Например, если имеются 3 ячейки и 2 предмета А и В, то получим следующую последовательность заполненных ячеек: (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3, 2). Т.е. А помещаем в 1-ю ячейку, В – во вторую, и т.д. Таким образом, =6.

Формула для числа всех размещений из п элементов по 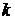элементов без повторений:

(1.2.1)

Доказательство.Для составления комбинации из к элементов

1-й элемент можно выбрать п способами,

2-й элемент можно выбрать способами,

3-й элемент можно выбрать способами,

……………………………………………..,

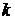-й элемент можно выбрать способами

(мы заметили, что вычитаемое все время на единицу меньше номера элемента).

По правилу произведения всего способов ч.т.д.

Замечание 1. Частный случай размещения: k=n. Тогда и по определению размещения, и по формуле (1.2.1) получим перестановку .

Пример 1.В ящике 9 пронумерованных от 1 до 9 шаров. Наугад вынимаются 3 шара, при этом номер каждого шара записывается. Сколько различных трехзначных чисел можно при этом получить?

Здесь Þ последний множитель в произведении (1.2.1) равен 7 Þ

.

Пример 2. Сколькими способами можно рассадить 50 студентов по 60 местам аудитории?

Замечание 2.Из формулы (1.2.1) можно получить другое выражение для вычисления размещений. Для этого умножим и разделим правую часть (1.2.1) на , а затем запишем множители числителя в обратном порядке:

(1.2.2)

.

Пример 3.Сколькими способами можно разместить 3 предмета А, В, С в 4 ячейках?

.

Сочетания

Сочетаниями из п элементов по 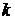элементов называются комбинации из 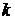элементов, которые отличаются друг от друга только составом элементов.

Из определения сочетания ясно, что порядок расположения элементов внутри комбинации не имеет значения, в отличие от размещения. В данном случае мы рассматриваем неупорядоченные множества из к элементов, выбранных из п-элементного множества. Сочетания обозначаются (це из эн по ка).

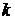Формула для числа всех сочетаний из по элементов:

. (1.3.1)

Доказательство.Докажем формулу:

(1.3.2)

Действительно, число всех размещений можно пересчитать следующим образом: сначала составим всевозможные сочетания; они будут отличаться только составом элементов; а затем внутри каждого сочетания проделаем всевозможные перестановки. Число этих способов по правилу произведения будет равно левой части формулы (1.3.2). Выразив из (1.3.2) сочетание , с учетом (1.2.2) получим искомую формулу (1.3.1).

Пример 1. Сколькими способами можно составить волейбольную команду из 8 игроков?

.

Пример 2. Сколькими способами в карточке спортлото 5 из 36 можно зачеркнуть 5 номеров (т.е. сколько нужно карточек)?

Число всех способов равно числу сочетаний (порядок зачеркивания не важен):

.

Таким образом, чтобы наверняка зачеркнуть нужную комбинацию из пяти номеров, нужно купить более 370 тысяч карточек.

Обобщение

Для лучшего понимания перестановок, размещений и сочетаний можно использовать схему:

Все ли элементы множества мы выбираем?

Сочетания

Важен ли порядок расположения элементов в подмножестве?

Размещения

Нет

Да

Нет

Да

СХЕМА КОМБИНАТОРИКИ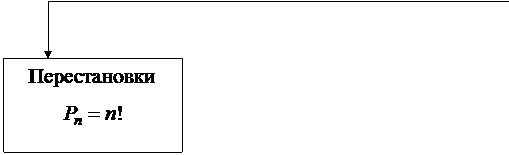

Тема: Случайные события

2. Случайные события

Испытания и события

Испытанием называется осуществление на практике какого-либо комплекса условий. В теории вероятностей изучаются только такие испытания, которые могут быть повторены, хотя бы теоретически, неограниченное число раз. В результате испытания наблюдают различные явления, которые называются событиями.

События делятся на детерминированные и случайные. Детерминированными событиями называются те, которые при неоднократном повторении испытания протекают каждый раз одинаково. Случайнымисобытиями называются события, которые могут произойти или не произойти в результате испытания по не зависящим от нас причинам.

Результатом каждого испытания является определённый исход- случайное событие, которое называется элементарным событием. В результате каждого испытания происходит одно и только одно элементарное событие. Элементарные события обычно обозначают строчными буквами w или е.

Пример 2.1.1.Подбрасывается монета (ее всегда будем считать круглой и однородной, а бросать её будем на твердую горизонтальную поверхность). В результате испытания могут быть следующие исходы: выпадение герба (орла) е_г и выпадение решки (нарицательной стоимости монеты) е_р. При математическом описании данного испытания естественно отвлечься от ряда несущественных исходов (монета встала на ребро, навсегда исчезла из вида, и т.д.) и ограничиться только двумя.

Пример 2.1.2.Испытание состоит в подбрасывании игральной кости. Предполагается, что выполнен следующий комплекс условий: игральная кость правильная, т.е. плотность вещества, из которого она сделана, постоянна, а её форма является идеальным кубом; на каждой грани этого куба написано одно и только одно из натуральных чисел от 1 до 6, кубик бросается на ровную гладкую поверхность. Эту первичную совокупность условий принято считать само собой разумеющейся, и никак не отмечать ее наличие. Элементарным событием является выпадение определённого числа очков от 1 до 6. Очевидно, что это событие является случайным.

Пример 2.1.3. Испытание состоит в вынимании одной карты из колоды. Комплекс условий: колода полная (36 или 52 карты), в ней 4 масти, и т.д. Элементарное событие – появление при этом определённой карты, например, дамы пик. Это случайное событие. Однако при раздаче карт шулером появление туза может оказаться не случайным, а детерминированным событием.

Виды случайных событий

Случайные события обозначаются заглавными буквами латинского алфавита: А, В, С, и т.д. Поскольку в дальнейшем мы будем иметь дело только со случайными событиями, вместо словосочетания «случайное событие» мы будем говорить просто «событие».

Невозможным называется событие, которое никогда не произойдёт в результате испытания. Обозначается Æ.

Пример 1.Выпадение числа 8 при бросании игральной кости.

Достоверным называется событие, которое обязательно произойдёт в результате испытания. Обозначается W.

Пример 2.Выпадение натурального числа при бросании игральной кости. Выпадение целого числа от 1 до 6 при бросании игральной кости.

Пример 3. Выбранное наугад трёхзначное число не больше 1000.

Два события называются несовместными, если наступление одного из них исключает наступление другого. Аналогично, п событий 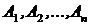называются попарно несовместными, если наступление одного из них исключает наступление любого другого.

Если наступление одного события не исключает наступление другого, то такие события называются совместными.

Пример 4. Если при единичном бросании игральной кости через 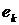обозначить событие, заключающееся в выпадении числа очков, равного 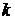, то события 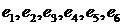будут попарно несовместными.

Пример 5.Событие А- выпадение на игральной кости числа очков, меньшего 5. Событие В – выпадение числа очков, большего 3. События А и В- совместны, т.к. выпадение четвёрки соответствует описанию обоих событий.

Пример 6. А- появление бубны при вынимании карты из колоды; В- появление трефы; С- пики; D -червы. События A, B, C, D попарно несовместны.

Пример 7.Выпадение чётного или нечётного числа очков при бросании кубика - несовместные события.

Операции над событиями

Поскольку событие отождествляется с множеством, то над событиями можно совершать все операции, выполнимые над множествами. Для геометрической иллюстрации действий над событиями, кроме таблиц, можно так же, как в теории множеств, использовать диаграммы Венна. Пространство (множество) элементарных событий будем считать некоторой областью на плоскости, например, прямоугольником, элементарные исходы - точками плоскости, лежащими внутри . При этом события – определённые совокупности (множества) точек - удобно изображать в виде множеств изолированных точек (рис.2.4.1, а, б) или сплошных фигур (рис.2.4.1, в). В обоих случаях соотношения между событиями будем трактовать как попадание точки в область, соответствующую этому событию. Приведём основные операции над событиями, указывая в скобках аналог из теории множеств.

а) б) в)

В

А В А

Рис.2.4.1

1. АÌВ (множество А есть подмножество множества В, А входит в В) - событие Авлечёт за собой событие В (рис.2.4.2). Иными словами, событие В происходит всякий раз, когда происходит событие А (событие А – частный случай события В).

АÌВ	АÈВ	АÈВ
Рис. 2.4.2	Рис.2.4.3	Рис.2.4.4

Событие А будет частью события В только в том случае, когда элементарные события, представляющие событие А, принадлежат подмножеству событий, представляющих событие В. (В содержит не меньше элементарных событий).

Пример 1.. Событие А – появление двух или четырёх очков при бросании игральной кости. Событие В – появление чётного числа очков при бросании

игральной кости. Здесь .

Пример 2. Мишень изображена на рисунке 2.4.5. Событие А – попадание в круг, В – в треугольник, С – в прямоугольник.

Тогда .

Рис.2.4.5.

Пример 3.Испытание состоит в произведении двух выстрелов по мишени (пример 5 с табличками). Рассмотрим события: А – попадание в мишень при 1-м выстреле, В – поражение мишени. Тогда .

2.А=В (соотношение эквивалентности множеств) – событие Атождественно событию В. Это возможно тогда и только тогда, когда и .

Пример 4.Событие А – выпадение герба. Событие В – невыпадение решки. А=В.

Пример 5. Событие А – выпадение 1, 3 или 5 при бросании кубика. Событие В – выпадение нечётного числа очков. А=В.

3.А+В (АÈВ- объединение множеств) – сумма событий. Это событие, состоящее в том, что произошло хотя бы одно из двух событий АилиВ (здесь неисключающее логическое или). Другими словами, произошло или А, или В, или А и В одновременно (рис.2.4.3, 2.4.4).

Пример 6.Событие А – выпадение числа 1 при бросании кубика. Событие В – выпадение числа 3. Событие А+В – выпадение нечётного числа, меньшего 5.

4. (АÇВ- пересечение множеств) – это произведение событий. Это событие, состоящее в совместном наступлении событий А и В (рис. 2.4.6, 2.4.7.).

А Ç В А Ç В

Рис.2.4.6 Рис.2.4.7

Пример 8.А – появление картинки при вынимании карты из колоды. В – появление бубны. АВ – появление бубновой картинки. Покажем это на диаграмме, выполненной в виде таблицы. Множеством элементарных событий в случае колоды из 36 карт будет множество всех карт колоды, т.к. элементарное событие - это появление одной карты. Изобразим это множество в виде таблицы, строками которой будут масти, а столбцами – достоинство (тип) карты:

тип масть	6	7	8	9	10	ВАЛЕТ	ДАМА	КОРОЛЬ	ТУЗ
пики	6п	7п	8п	9п	10п	Вп	Дп	Кп	Тп
трефы	6т	7т	8т	9т	10т	Вт	Дт	Кт	Тт
бубны	6б	7б	8б	9б	10б	Вб	Дб	Кб	Тб
черви	6ч	7ч	8ч	9ч	10ч	Вч	Дч	Кч	Тч

Тогда событие А (картинка) будет изображаться четырьмя последними столбцами, событие В (бубна) – третьей строкой таблицы. Произведение АВ (бубновая картинка) – пересечением этих множеств, т.е. четырьмя последними клетками третьей строки.

Пример 9. А – выбранное число кратно 2. В – выбранное число кратно 3. - выбранное число кратно 6.

А - В

Рис.2.4.8. Рис.2.4.9. Рис.2.4.10.

5. ( А \ В)-множество элементов, принадлежащих А, но не принадлежащих В – разность событий. Это событие, состоящее в том, что А происходит, а В не происходит (рис.2.4.8).

Пример 10.А – выпадение нечётного числа очков при бросании кубика. В – выпадение 1 очка. А–В – выпадение 3 или 5 очков.

6. (дополнение множества А до ) – противоположное событие, состоящее в том, что событие А не происходит (рис.2.4.9, 2.4.10). Из определения ясно, что сумма противоположных событий – достоверное событие (при испытании обязательно произойдет либо А, либо все, кроме А). Произведение противоположных событий – невозможное событие, т.к. А и 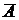- несовместные события.

. В частности, .

Пример 11. А – появление трефы при вынимании карты из колоды. – появление пики, червы или бубны (любой масти, кроме трефы).

Пример 12. А – попадание в мишень двумя выстрелами из двух. – попадание одним выстрелом из двух или 2 промаха.

Пример 13.А – хотя бы одно попадание при 2 выстрелах. – ни одного попадания (2 промаха).

7. Другое определение несовместных событий.События А и В называются несовместными, если (рис.2.4.11). Это означает, что не существует ни одного элементарного события, принадлежащего и А, и В.

Аналогично события называются попарно несовместными, если для любых . Таким образом, для попарно несовместных событий можно записать:

Ясно, что два несовместных события являются частным случаем попарно несовместных событий.

Пример 13.. А – срок службы прибора менее 1 года. В – срок службы прибора более 5 лет.

Пример 14.А – два попадания в мишень при двух выстрелах. В – 2 промаха при двух выстрелах.

Из рис.2.4.11 видно, что события А и В не пересекаются, следовательно, суммой двух несовместных событий является событие, осуществляющееся в появлении либо события А, либо события В. Можно также воспользоваться исключающим логическим или (XOR).

8.Два события А и В называются совместными, если существует по крайней мере одно элементарное событие, входящее в произведение А и В, т.е. благоприятствующее и событию А, и событию В. Совместные события всегда имеют непустое пересечение.

Пример 15.А – число выпавших очков на кубике больше 3. В – число выпавших очков на кубике меньше 5. Элементарное событие благоприятствует А и В.

Понятия произведения и суммы можно распространить на бесконечные последовательности (счётные множества) событий. Событие

состоит в том, что произошло хотя бы одно из событий .

Событие

состоит в том, что все события произошли одновременно.

9. Полная группа событий. Совокупность событий называется полной группой событий, если:

1. Они попарно несовместны, т.е. ,

2. Их сумма (объединение) – достоверное событие, т.е. .

Замечание 1.Если два события A и B составляют полную группу событий, то , т.е. A и B – противоположные события. Действительно, не пересекаются, а .

Замечание 2. Множество всех исходов одного испытания образуют полную группу. Действительно, результатом испытания является один и только один исход. Исходы не пересекаются, а в результате испытания обязательно произойдёт один из них.

Полная группа событий изображена на рис.2.4.12. Круг на первом рисунке и большой прямоугольник на втором рисунке означают пространство элементарных событий (достоверное событие). Секторы круга на первом рисунке и клетки прямоугольника на втором означают события, образующие полную группу.

Пример 16. Появление мастей П, Ч, Т, Б – полная группа событий. Красные и чёрные масти карт тоже образуют полную группу. Кроме того, карты одинакового достоинства: шестёрки, семёрки,..., тузы.

Рис.3.1.1

Пример. В урне белые, чёрные и красные шары. Вынимается по одному шару. Белый шар появился k раз, чёрный т раз. Событие «белый или чёрный шар» произошло k+т раз.

Следствия из аксиом

При доказательстве следствий из аксиом мы будем пользоваться следующими тождествами, которые встречались нам при изучении действий над событиями:

АW=А, А+ =W,(А+В)С=АС+ВС, .

Следствие 1. Если составляют полную группу событий, то сумма их вероятностей равна единице:

. (4.2.1)

Следствие 2. Сумма вероятностей противоположных событий равна 1.

(4.2.5)

Следствие 3.Вероятность невозможного события равна нулю.

Следствие 4.Если ВÌА, т.е. В является частным случаем А (или В влечет за собой А), то

.

Рис.4.2.1 Рис.4.2.2 Рис.4.2.3

Следствие 5. Для произвольных случайных событий А и В

(4.2.9)

А=А×W=А(

(рис.4.2.2). Справа получена сумма несовместных событий, следовательно, по аксиоме 3

, ч.т.д.

Следствие 6.Теорема сложения для произвольных событий. Для любых событий А, В

Р(А+В)=Р(А)+Р(В)-Р(АВ). (4.2.10)

Замечание.Если А и В несовместны, то получаем аксиому 3, т.к. в этом случае .

Тема: Схема равновозможных исходов

Доказательство.

а) б)

е1	е2	е3
		ет	ет+1	ет+2
				еп

Рис.4.3.1

А=е₁+е₂+…+е_m

Вычислим вероятность события А. События е₁, е₂, …,е_n являются попарно несовместными, следовательно, по аксиоме 3

.

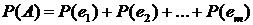Обозначим вероятность всех исходов буквой р (эти вероятности равны, т.к. исходы по условию равновозможны). Заметим, что вероятность р нам неизвестна. Тогда

Р(А)=mp (4.3.2)

С другой стороны, т.к. W= е₁+е₂+