Критерий подобия Рейнольдса, Фруда, Эйлера, Вебера

Критерий Ньютона Ne выражает зависимость между силами, массами, скоростями и линейными размерами в динамически подобных потоках в общем виде. В гидравлике приходится иметь дело главным образом с тремя видами сил: силой веса, силой давления и силой трения. В некоторых случаях приходится принимать во внимание силы поверхностного натяжения. При этом чаще всего в различных явлениях главную роль играет только один из этих видов сил. В общем, идеальном, случае полного подобия необходимо иметь подобие всех сил. Однако каждый их этих видов сил требует своих условий подобия, причем иногда несовместимых. Таким образом, удовлетворить основному условию подобия – равенству критериев Ньютона – не всегда возможно. В таких случаях необходимо обеспечить подобие того вида сил, который оказывается наиболее существенным в изучаемом явлении.

Критерии частичного подобия можно получить из критерия Ньютона, подставив в него, например, вместо силы F силу трения 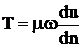, при этом получим условие подобия только сил трения (критерий Рейнольдса – Re), или силу тяжести G=mg – получим условие подобия только сил тяжести (критерий Фруда – Fr), или силу давления Р=р - условие подобия только сил давления (критерий Эйлера – Eu).

Подставим в выражение (8.1) силу трения Т:

.

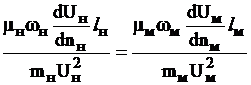Имея в виду, что 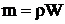, а в подобных системах

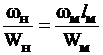и ,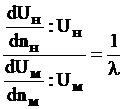

будем иметь

,

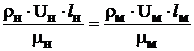где 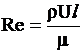- критерий Рейнольдса.

Таким образом, подобие сил трения в потоках, удовлетворяющих условиям геометрического, кинематического и материального подобия, будет только в том случае, если для каждой пары соответственных точек потока натуры и модели число Рейнольдса будет иметь одно и то же значение. В числе Рейнольдса за величину U может быть принята средняя скорость потока V, а за l - любая характерная линейная величина. Например, при изучении законов движения жидкости в трубах применяется диаметр трубы d или гидравлический радиус R. При этом число Рейнольдса будет представлено в виде

; .

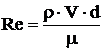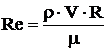Следует иметь в виду, что для подобия двух явлений существенно не численное значение критерия, а лишь его равенство для потоков натуры и модели.

Подставив в выражение (8.1) силу тяжести G = mg, получим

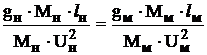
или после сокращения

,

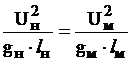где 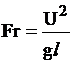- критерий (число) Фруда.

Иногда число Фруда выражают через среднюю скорость:

.

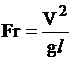Равенство числа Фруда (Fr) в соответствующих точках потоков, удовлетворяющих геометрическому, кинематическому и материальному подобию, обеспечивает подобие сил тяжести. За величину l может быть принята любая характерная линейная величина.

Подставив в выражение (8.1) силу давления Р = р , получим

.

Имея в виду, что 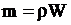и, кроме того, в геометрически подобных системах 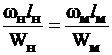, найдем

,

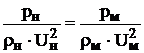где 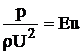- критерий (число) Эйлера.

Числу Эйлера придают несколько иной вид, введя вместо абсолютного давления р разность давления Δр:

.

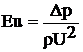Число Эйлера играет большую роль в исследовании явлений, связанных с кавитацией. В этом случае за Δp принимается Δp = p - р_п, где р_п – давление парообразования. Число k=2Еu называется числом кавитации. Таким образом, равенство чисел Эйлера обеспечивает в динамически подобных потоках подобие сил давления.

В некоторых гидравлических исследованиях существенное значение имеет поверхностное натяжение. Для получения соответствующих условий подобия можно также исходить из критерия Ньютона, подставляя в него значение силы поверхностного натяжения F= 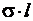, где σ - коэффициент поверхностного натяжения. Преобразования позволяют получить число Вебера – критерий подобия сил поверхностного натяжения в виде

,

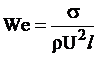где l - характерная линейная величина.

Раздел 2

Гидравлические машины

гидравлические машины делятся на два класса: насосы и гидродвигатели.

Насосы

Насос – это гидравлическая машина, которая служит для преобразования механической энергии двигателя в энергию перемещаемой жидкости.

насосы являются одной из самых распространенных разновидностей машин. Их используют для различных целей: подачи воды для водоснабжения и орошения, отвода ее с осушительных систем, для работы гидравлического транспорта и систем теплоснабжения. Это силовая часть гидравлических приводов. Системы смазки и охлаждения двигателей внутреннего сгорания немыслимы без насосов.

Конструктивное разнообразие насосов чрезвычайно велико.

9.1. Классификация насосов

Классификация насосов согласно государственному стандарту дана с точки зрения принципа их действия. При этом прослеживаются и конструктивные признаки (рис. 9.1).

Насосы

Динамические

Объемные

лопастные

трения

возвратно-поступательные

роторные

центробежные

осевые

диагональные

вихревые

струйные

шнековые

эрлифты

дисковые

поршневые

плунжерные

диафрагменные

шестеренные

шиберные

аксиально-поршневые

радиально-поршневые

Рис. 9.1

Основные параметры насосов

Основными выходными параметрами насосов, характеризующими их работу как гидравлической машины, являются подача Q, м³/с, л/с, л/мин; напор (давление) Н(р), м в.ст (Па); мощность N, кВт и коэффициент полезного действия η.

Параметр «напор» характерен для насосов динамических, «давление» - для объемных.

Напор, развиваемый насосом

Необходимость в определении напора возникает в двух случаях: при эксплуатации насосной установки; при проектировании насосной установки.

Напор, развиваемый насосом, есть разность удельных энергий на выходе и входе насоса: Н = Е_вых-Е_вх (рис.9.2).

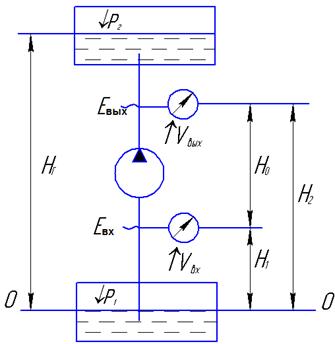
Рис.9.2

Согласно уравнению Бернулли для выходного и входного сечений, где установлены приборы для измерения давлений, относительно плоскости сравнения О-О эти энергии можно определить по выражениям

;

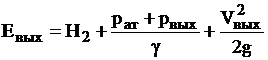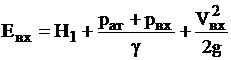(p_вх>р_ат).

Тогда

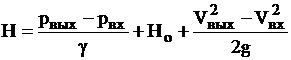. (9.1)

Если р_вх<р_ат, т.е. на входе в насос установлен вакуумметр, то 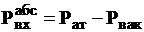. тогда

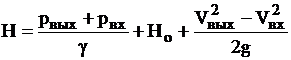. (9.2)

По выражениям (9.1) и (9.2) определяется напор при эксплуатации насосной установки.

При проектировании насосной установки напор насоса определяется из выражения

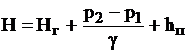, (9.3)

где Н_г – геометрическая высота подъема; р₁, р₂ – давление на свободных поверхностях; h_п – гидравлические потери.

Мощность и КПД насоса

Так как насос является преобразователем механической энергии в гидравлическую (рис. 9.3), то такое преобразование всегда связано с потерей энергии. К насосу подводится мощность N, а после насоса отводится полезная N_п в виде гидравлической, т.е. N_п<N (рис. 9.4). Такое неравенство оценивается коэффициентом полезного действия насоса η, т.е. ;

N_п= QH=рQ.

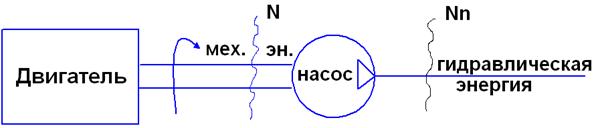
Рис.9.3

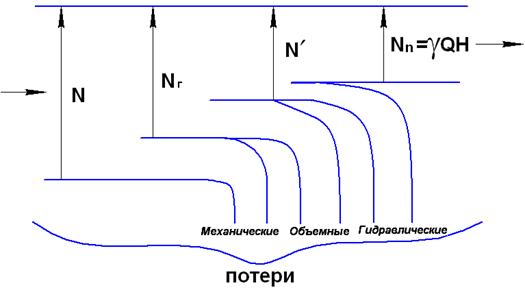
Рис.9.4

Часть подведенной мощности теряется (превращается в тепло). Потери мощности в насосе делят на механические, объемные и гидравлические.

Механические потери.Механическими потерями являются потери на трение в подшипниках, в уплотнениях вала и на трение элементов насоса о жидкость.

Мощность N_г, остающаяся за вычетом механических потерь, передается рабочими органами насоса жидкости. Ее принято называть гидравлической.

Величина механических потерь оценивается механическим КПД, который равен отношению оставшейся после преодоления механических сопротивлений гидравлической мощности N_г к мощности N, подведенной к насосу:

.

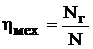численное значение η_мех = 0,70…0,98.

Объемные потери.Жидкость, выходящая из рабочих элементов насоса, например, из рабочего колеса насоса, в основном поступает в напорный патрубок насоса, но частично возвращается снова на вход насоса через зазоры. Энергия этой возвращающейся жидкости теряется. Эти потери называются объемными. Утечки обусловлены тем, что давление на выходе больше, чем на входе. Кроме того имеются утечки через уплотнение вала. Они обычно малы, и ими можно пренебречь.

Объемные потери оценивают объемным КПД, равным отношению мощности 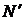, оставшейся за вычетом мощности, затрачиваемой на объемные потери, к гидравлической мощности N_г:

,

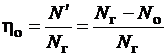где N_о – мощность, затрачиваемая на объемные потери.

Так как каждая единица веса жидкости, протекающей через зазоры и уплотнения, уносит Н_т энергии, то объемный к.п.д. можно выразить как ,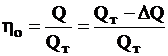

где Q_Т – теоретическая подача; ΔQ – утечки.

численное значение 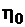= 0,90…0,98.

Меньшее значение к.п.д. характерно для динамических насосов, большее – для объемных.

Гидравлические потери.Третьим видом потерь энергии в насосе являются потери на преодоление гидравлического сопротивления подвода, рабочих элементов насоса, например, рабочего колеса лопастных насосов и отвода, или гидравлические потери. Они оцениваются гидравлическим к.п.д. η_г, который равен отношению полезной мощности насоса N_п к мощности N`:

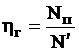или ,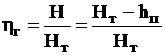

где h_п – гидравлические потери; численное значение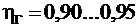

Тогда полный к.п.д. насоса 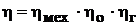; η = 0,35…0,96. меньшее значение характерно для насосов трения, большее – для крупных насосов.

Мощность насоса, т.е. мощность, которую необходимо подвести к насосу, определяют из выражения

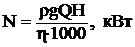или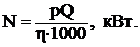

размерность величин: ρ, кг/м³; g, м/с²; Q, м³/с; Н, м.

Двигатель к насосу должен быть выбран с некоторым запасом мощности К:

N_дв = К N.

Численное значение коэффициента запаса мощности от мощности насоса N:

N, кВт	<1	1-2	2-5	5-50	>50
К		1,5	1,2	1,15	1,1

Область применения насосов

С целью того, чтобы сузить поиск необходимого насоса для той или иной цели рассмотрим область применения различных групп насосов согласно классификации, в зависимости от их основных параметров: подачи Q и напора Н.

Если говорить о возможной подаче, то по мере ее увеличения насосы располагаются в следующем порядке (рис.9.5): объемные, центробежные и осевые. Если же в качестве определяющего параметра рассматривать максимально возможное значение напора, то порядок будет обратным. Что касается насосов трения, то все они в поле Н - Q занимают области, прилегающие к осям координат и характеризуемые малыми значениями либо напора, либо подачи. Таким образом, практически весь диапазон напоров от 1 до 10000 м и подача от нескольких литров до 150000 м³/ч перекрывается большим числом типоразмеров хорошо освоенных промышленностью насосов.

.

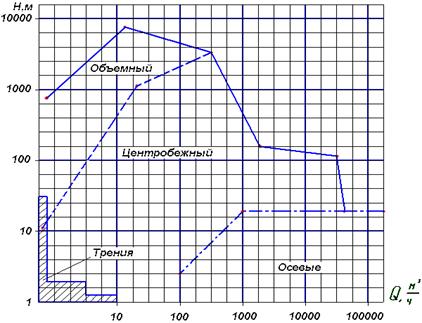
Рис. 9.5

Динамические насосы

Из этой группы насосов более подробно изучаются центробежные насосы, входящие по классификации в подгруппу лопастных насосов, поэтому определению «центробежный насос» должны предшествовать определения «Динамический насос» и «Лопастной насос» согласно ГОСТ 17398-72.

Центробежные насосы