Г о с у д а р с т в е н н о г о э к з а м е н а
П Р О Г Р А М М А
Г о с у д а р с т в е н н о г о э к з а м е н а
По специальности 1-31 03 01 «Математика»
Программа утверждена Советом
математического факультета
Протокол № 7
от ““ 2012 г.
Декан математического факультета
___________ С.П.ЖОГАЛЬ
Гомель 2012
На государственном экзамене выпускник должен продемонстрировать умение систематизировать информационные сведения программы экзамена, знание основных теорем и понятий, понимание взаимосвязей между ними, умение ими пользоваться.
С учетом этих требований экзаменующийся по каждому вопросу билета должен сделать обзор материала, соответствующего формулировке вопросов, сопровождая ответ доказательством отдельных теорем.
Математический анализ
1. Числа натуральные, рациональные и действительные. Полнота множества действительных чисел.
2. Последовательности и их сходимость (сходящиеся последовательности в топологическом пространстве; сходящиеся последовательности действительных чисел; теорема о существовании предела монотонной ограниченной последовательности; свойства последовательностей действительных чисел, связанные с арифметическими операциями над последовательностями).
3. Числовые ряды (сходимость числовых рядов; сходимость рядов с неотрицательными членами, признаки их сходимости; абсолютно сходящиеся ряды, их свойства; условно сходящиеся ряды).
4. Производная функции в точке. Дифференциал. Производные и дифференциалы высших порядков.
5. Основные теоремы дифференциального исчисления: Ферма, Ролля, Лагранжа и Коши. Формула Тейлора.
6. Непрерывные функции. Свойства функций, непрерывных на отрезке.
7. Интеграл Римана (определение, существование, свойства; дифференцируемость интеграла Римана по верхнему пределу). Существование первообразной у непрерывной функции. Формула Ньютона-Лейбница.
8. Дифференцируемость функций нескольких переменных (частные производные и дифференциалы функций многих переменных; необходимые условия дифференцируемости функций многих переменных; достаточные условия дифференцируемости).
9. Формула Тейлора для функций нескольких переменных. Достаточные условия локального экстремума.
10. Производные и дифференциалы высших порядков функции многих переменных. Необходимые и достаточные условия экстремума функции многих переменных.
11. Равномерная сходимость функциональных последовательностей и рядов (критерий Коши равномерной сходимости функциональных последовательностей и рядов; признак Вейерштрасса равномерной сходимости функционального ряда).
12. Двойной интеграл Римана (сведение двойного интеграла к повторному; замена переменных в двойном интеграле; кратные интегралы).
13. Криволинейные и поверхностные интегралы (формула Грина; условия независимости криволинейного интеграла от формы пути).
14. Криволинейные и поверхностные интегралы. Формула Остроградского. Формула Стокса.
Функциональный анализ и интегральные уравнения
1. Мера. Мера Лебега на прямой. Интеграл Лебега: определение и свойства.
2. Метрические пространства. Непрерывные функции. Свойства функций, непрерывных на компакте.
3. Нормированные пространства (банаховы пространства; гильбертовы пространства; ортогональные системы; ряды Фурье; равенство Парсеваля; неравенство Бесселя).
4. Линейные функционалы и операторы (норма оператора; связь непрерывности линейного оператора с его ограниченностью; теорема Банаха-Штейнгауза (принцип равномерной ограниченности); теорема Банаха об обратном операторе).
5. Компактные операторы. Альтернатива Фредгольма.
Теория функций комплексного переменного
1. Производная функции комплексного переменного. Аналитичность. Степенной ряд, круг его сходимости. Ряд Тейлора.
2. Интегральная теорема Коши. Разложение аналитической функции в ряд Тейлора. Интегральная формула Коши.
3. Ряд Лорана. Особые точки. Вычет. Применения теории вычетов. Разложение аналитической функции в ряд Лорана.
Алгебра и теория чисел
1. Основные алгебраические структуры (аддитивная и мультипликативная группы, кольца, поля: определения и примеры).
2. Делимость в кольце целых чисел (определение делимости; теорема о делении с остатком; алгоритм Евклида; нахождение наибольшего общего делителя двух целых чисел с помощью алгоритма Евклида; связь наибольшего общего делителя и наименьшего общего кратного двух натуральных чисел; разложение натурального числа на простые множители и его единственность (основная теорема арифметики)).
3. Кольцо классов вычетов (определение сравнимости двух целых чисел по натуральному модулю; свойства сравнений; классы вычетов; операции на классах вычетов; кольцо классов вычетов).
4. Поле комплексных чисел (операции над комплексными числами в алгебраической и тригонометрической формах; формула Муавра; извлечение квадратного корня из комплексного числа в алгебраической форме; извлечение корня n-ой степени из комплексного числа в тригонометрической форме).
5. Определители (формула определителя квадратной матрицы; вычисление определителей малых порядков; вычисление определителя разложением по строке (столбцу); теорема об определителе произведения матриц; обратимые матрицы; вычисление обратной матрицы с помощью алгебраических дополнений).
6. Системы линейных уравнений (совместные, несовместные и равносильные системы; критерий совместности системы линейных уравнений (теорема Кронекера-Капелли); крамеровская система; правило Крамера и матричный метод решения крамеровских систем; однородная система линейных уравнений; условия существования ненулевого решения однородной системы линейных уравнений).
7. Кольцо многочленов от одной переменной (теорема о делении с остатком, алгоритм Евклида и нахождение наибольшего общего делителя двух многочленов с его помощью; корни многочленов; теорема Безу; основная теорема алгебры комплексных чисел (теорема Гаусса) и её следствия; комплексные корни многочленов с действительными коэффициентами).
8. Векторное пространство над полем, примеры (понятие подпространства; линейная зависимость векторов; базис векторного пространства; понятие размерности; координаты вектора; евклидовы и унитарные пространства; длина вектора; теорема Коши-Буняковского; ортонормированные базисы).
9. Линейные отображения (ядро и образ линейного отображения; ранг и дефект линейного оператора, примеры; матрица линейного оператора; собственные векторы и собственные значения линейных операторов; ортогональные и самосопряженные линейные операторы; теорема об ортогональных и самосопряженных линейных операторах).
10. Квадратичные формы (преобразование квадратичной формы при линейном однородном преобразовании переменных; канонический вид квадратичной формы; закон инерции квадратичных форм (индекс инерции квадратичных форм); нормальный вид действительных и комплексных квадратичных форм; положительный и отрицательный индексы инерции действительных квадратичных форм; положительно определенные квадратичные формы).
Аналитическая геометрия
1. Различные виды уравнений прямой на плоскости (общее; по двум точкам; по угловому коэффициенту и точке; каноническое; параметрические; в отрезках по осям).
2. Плоскость и ее уравнения. Взаимное расположение прямых и плоскостей в пространстве.
3. Кривые второго порядка (упрощение общего уравнения линии второго порядка с помощью преобразования системы координат; канонические уравнения кривых второго порядка).
Основания геометрии
1. Аксиоматический метод. Аксиоматическое построение евклидовой геометрии (системы аксиом Гильберта и Вейля). Геометрия Лобачевского. Модель Кэли-Клейна.
Дифференциальные уравнения
1. Понятие дифференциального уравнения и его решения. Интегрируемые типы уравнений (уравнения с разделяющимися переменными; линейные дифференциальные уравнения, дифференциальные уравнения Бернулли).
2. Основные теоремы теории дифференциальных уравнений: теорема существования и единственности решения задачи Коши и методы ее доказательства; теоремы о характере зависимости решения от параметров и начальных данных (приводятся формулировки этих теорем и выясняется их роль в теории дифференциальных уравнений).
3. Принцип суперпозиции для линейных уравнений и систем (приводятся формулировки соответствующих теорем и даются доказательства не менее двух из них; выясняется их роль в теории линейных дифференциальных уравнений). Метод Лагранжа для уравнений и систем (излагается сущность метода, приводится доказательство соответствующей теоремы для уравнения или системы (по выбору)).
4. Фундаментальная система решений линейного однородного дифференциального уравнения и его общее решение (приводятся формулировки и доказательства). Фундаментальная система решений линейной однородной системы и общее решение этой системы.
5. Решение линейных дифференциальных уравнений с постоянными коэффициентами (излагается метод решения и дается обоснование этого метода соответствующими теоремами). Решение линейных систем с постоянными коэффициентами.
6. Первые интегралы дифференциальных систем и основные теоремы о них.
Теоретическая механика
1. Способы задания движения точки. Вычисление скорости и ускорения материальной точки при различных способах задания движения.
2. Основные теоремы динамики точки: теорема об изменении кинетической энергии, теорема об изменении количества движения и теорема об изменении кинетического момента.
3. Уравнения Лагранжа второго рода для системы материальных точек.
ЛИТЕРАТУРА
Математический анализ
1. Никольский С.М. Курс математического анализа: Учеб.пособие в 2-х томах, 3-е издание. М., Наука, 1983.
2. Кудрявцев Л.Д. Курс математического анализа: Учебник в 2-х т. М. Высш.школа. 1981.
3. Зорич В.А. Математический анализ: Учебник в 2-х т. М.: Наука, 1981, 1984.
4. Рудин У. Основы математического анализа. М.: Мир, 1976. 319 с.
Теоретическая механика
1. Бухгольц, Н.Н. Основной курс теоретической механики: В 2-х ч. [Текст] / Н.Н.Бухгольц – М.: Наука, 1972.
2. Тарг, С.М. Краткий курс теоретической механики [Текст] / С.М.Тарг – М.: Наука, 1976.
3. Яблонский, А.А. Курс теоретической механики, ч. 1, 2. [Текст] / А.А.Яблонский – М.: Наука, 1971.
Дифференциальные уравнения
1. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. Минск: Вышэйшая школа, 1974.
2. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М.: 1984.
ПЕРЕЧЕНЬ ЗАДАЧ
Математический анализ
1. Найти предел 
.
2. Найти предел  .
.
3. Найти точки разрыва функции  , установить их род и указать скачки в точках разрыва первого рода, если
, установить их род и указать скачки в точках разрыва первого рода, если
 .
.
4. Является ли функция 

 непрерывной на
непрерывной на  ? Дифференцируемой на
? Дифференцируемой на  ? Найти ее производную в тех точках, где производная существует.
? Найти ее производную в тех точках, где производная существует.
5. Проведя исследование, построить график функции
 .
.
6. Вычислить следующие интегралы:
а) 
 б)
б)  .
.
7. Найти  где
где 

8. Вычислить  .
.
9. Найти площадь фигуры, ограниченной кривыми
y = 2x – x2 , x + y = 0.
10. Исследовать сходимость интеграла

11. Найти  , если
, если

12. Найти:  .
.
13. Исследовать на сходимость  .
.
14. Исследовать ряд на сходимость
 .
.
15. Исследовать на сходимость  .
.
16. Найти области сходимости функционального ряда и его сумму и исследовать ее на непрерывность

17. Доказать равномерную сходимость ряда в указанном промежутке

18. Написать ряд Фурье функции
 на отрезке
на отрезке 

19. Найти  , если
, если  .
.
20. Найти дифференциал d3u, если u = x3 + y3 + xy(x - y)
21. Изменить порядок интегрирования в повторном интеграле

22. Вычислить  , где 0 начало координат и точка A (1,1)по следующим кривым:
, где 0 начало координат и точка A (1,1)по следующим кривым:
а) ОА - отрезок прямой линии;
б) ОА - парабола, ось которой есть OY;
в) ОА - ломаная линия, состоящая из отрезков ОВ, оси ОХ и отрезка ВА, параллельного оси OY.
23. Применяя формулу Грина, вычислить криволинейный интеграл
 , где
, где  - окружность x2 + y2 = 1.
- окружность x2 + y2 = 1.
24. Вычислить пределы:
а)  ; б)
; б)  .
.
25. Существуют ли такие a и b, при которых функция

всюду дифференцируема?
26. Исследовать на дифференцируемость функцию

Алгебра и теория чисел
1. Исследовать систему на совместимость и решить методом Крамера.
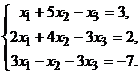
2. Решить систему линейных алгебраических уравнений методом Гаусса

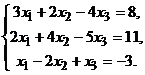 .
.
3. Разложить пространство R4 на прямую сумму подпространств размерности 2.
4. Докажите, что в пространстве M(2, R) система векторов 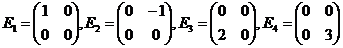 линейно независима.
линейно независима.
5. Найдите жорданову нормальную форму матриц: 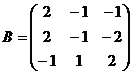 .
.
6. Исследовать, являются ли векторы
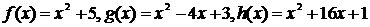
векторного пространства 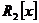 линейно зависимыми.
линейно зависимыми.
7. Найти собственные значения и собственные векторы линейного оператора пространства R2, заданного в некотором базисе матрицей
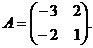 .
.
8. Найти все значения 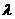 , при которых вектор
, при которых вектор 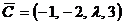 линейно выражается через векторы
линейно выражается через векторы
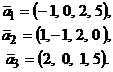
9. Найти базис и размерность линейной оболочки 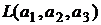 векторов из
векторов из 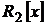 , где
, где 
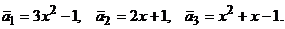
10. Докажите, что линейные пространства 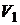 и
и 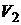 изоморфны:
изоморфны:
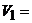 C над R ,
C над R , 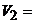 R2.
R2.
11. Найти матрицу, обратную матрице А
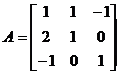 .
.
12. Вычислить: а) 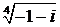 ; б)
; б) 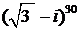 .
.
13. С помощью алгоритма Евклида найти наибольший общий делитель (96,165) и выразить его через исходные числа.
14. Составить таблицы сложения и умножения в кольце классов вычетов 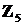 .
.
15. Даны два базиса 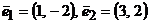 и
и 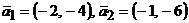 пространства
пространства 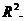
Найти матрицу перехода от базиса 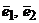 к
к 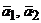 .
.
16. Найти ранг матрицы А
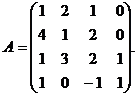
Аналитическая геометрия
1. Вычислите длины диагоналей параллелограмма, построенного на векторах 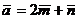 и
и 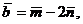 где
где 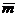 и
и 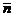 – единичные векторы, угол между которыми 600.
– единичные векторы, угол между которыми 600.
2. Вычислите площадь параллелограмма, диагонали которого определяют векторы 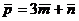 и
и 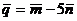 , если
, если 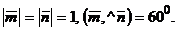
3 .Составьте уравнение прямой, проходящей через точку А (12, 6) так, чтобы площадь треугольника, образованного ею и координатными осями, была равна 150 кв. ед.
4. Найдите основание перпендикуляра, проведенного из точки А (1, 3, 5) к прямой, по которой пересекаются плоскости 2x + 2y + z – 1 = 0,
3x + y +2z – 3 = 0.
5. Найдите расстояние между скрещивающимися прямыми:
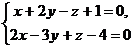 и
и 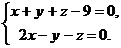
6. Через прямую x = 2 + 5t, y = 3 + t, z = –1 + 2t проведите плоскость, перпендикулярную к плоскости 4x + 3y – z + 3 = 0.
7. Какая плоская фигура задана уравнением:
x2 – 4y2 + 4x + 24y – 36 = 0.
Дифференциальные уравнения
1. Проинтегрировать следующие системы дифференциальных уравнений:

2. Проинтегрировать следующую систему дифференциальных уравнений:

3. Найти решение указанной ниже задачи:

4. Найти решение указанной ниже задачи:

5. Найти решение указанной ниже задачи:

6. Найти решение указанной ниже задачи:

7. Найти решение указанной ниже задачи:

8. Найти решение указанной ниже задачи:

9. Проинтегрировать следующее уравнение:

Теоретическая механика

1. Определить реакцию опоры  в
в  , если момент пары сил
, если момент пары сил  , интенсивность распределённой нагрузки
, интенсивность распределённой нагрузки  , размеры
, размеры  ,
,  .
.
2. Дифференциальное уравнение колебательного движения материальной точки имеет вид  . Определить период затухающих колебаний.
. Определить период затухающих колебаний.
3. Тело массой  падает по вертикали, сила сопротивления воздуха
падает по вертикали, сила сопротивления воздуха  . Определить максимальную скорость падения тела.
. Определить максимальную скорость падения тела.
П Р О Г Р А М М А
г о с у д а р с т в е н н о г о э к з а м е н а
