Разрывные функции, точки разрыва и их виды.

Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.

Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.

Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

Исследование функции на непрерывность. Показать на примере.

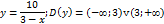
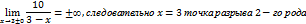
Асимптоты к графику функции

Асимптота - прямая, к которой график ф-ции стремится, но никогда ее не пересекает.

1) прямая х=х₀ назыв-ся вертикальной асимптотой графика ф-ции f(x)=y, если при х®х₀ |f(x)|®+¥ (вида x=b)

2) y=kx+b, ,y=f(x) - общее ур-е наклонной асимптоты

lim[f(x)-(kx+b)]=0, f(x)=kx+b+a(б.м.в.) по св-ву x®¥ пределов.

разделим левую и правую части на х. Возьмем предел при х®¥

f(x)/x=k+b/x+a/x, lim(f(x)/x)=limk+lim(b/x)+lim(a/x)

x®¥

, то

k=lim(f(x)/x)

b=lim[f(x)-kx]

Если эти пределы существуют, то существует и наклонная ассимптота вида kx+b=y

3)k=lim(f(x)/x)=0, y=b - горизонтальная асимптота.

Определение производной функции, нахождение производной по определению.

Геометрический смысл производной.

Геометрический смысл производной.

KN=Dy, MK=Dx

DMNK/tg2=Dy/Dx

вычислим предел левой и правой части:

limtga=lim(Dy/Dx) Dx®0

tga₀=y`

a®a₀

При Dx®0 секущая MN®занять положение касательной в точке M(tga₀=y`, a®a₀)

Геометрический смысл производной заключается в том, что есть tg угла наклона касательной, проведенной в точке x₀.

Физический смысл I и II производных.

V(t)=s’(t)

a(t)=s’’(t)

Уравнение касательной.

Уравнение нормали.

y-f(x₀)=-1/f’(x₀)(x-x₀)

Производная сложной функции (на примерах).

Производная неявной функции (на примерах).

Производные высших порядков (на примерах).

Производные высших порядков (показать на примерах)

Дифференциал функции и его вычисление.

Дифференциалом ф-ции наз. величина, пропорциональная б.м. приращению аргумента Dх и отличающаяся от соответствующего приращения ф-ции на б.м.в. более высокого порядка малости, чем Dх.

Геометрический смысл дифференциала функции.

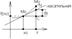Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x₀,f(x₀)) при изменении x₀ на величину Dx.Если непрерывная кривая, имеющая в каждой точке касательную, пересекает ось 0х в точках х=а и х=b, то на этой кривой найдётся хотя бы одна точка с абциссой с(а<c<b), в которой касательная || оси 0х.

Приближенные вычисления с помощью дифференциала