Распределение Пуассона. Простейший поток событий.

Говорят, что случайная величина Х имеет распределение Пуассона, если её возможные значения 0, 1, 2, ... , т, ... (бесконечное, но чёткое множество значений), а соответствующие вероятности выражаются формулой:

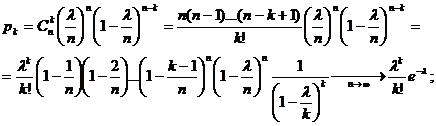
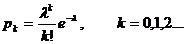
x			…	k	…
P	e-l	le-l	…		…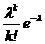

Число l называется параметром распределения.

Простейший поток событий – такая последовательность событий, происходящих в случайный момент времени.

Поток событий называется пуассоновским, если он удовлетворяет аксиомам простейшего потока событий:

При таких допущениях с большой степенью точности выполняются следующие условия:

1. Отсутствие последействия: вероятность того, что на произвольном временном промежутке (с точки зрения длины и расположения на временной оси) не зависит от того, что происходило в момент времени, предшествующему этому моменту.

2. Однородность потока: Вероятность того, что на некотором временном промежутке произойдет 0,1,2,…,n событий зависит только от его длины и не зависит от положення этого отрезка на временной оси.

3. Пусть Dt - длина временного промежутка, тогда: 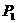(Dt)=l Dt+o(Dt), Dt®0.

4. 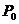(Dt)=1-l Dt+o(Dt), Dt®0.

Математическое ожидание распределения Пуассона равно:

M =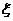

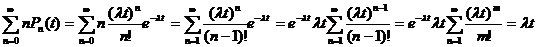
41. Отдельные числовые значения аргумента или признака, по которому совокупность подразделяют на группу, называют его вариантами и обозначают через x₁, x₂, ..., x_k.

Количество элементов совокупности, имеющих одинаковое числовое значение, называется частотой данной варианты; частоты обозначили через n₁, n₂, ..., n_k; n₁ + n₂ + ... + n_k = n. Отношение частоты варианты к объему совокупности назвали относительной частотой варианты и обозначили через v₁, v₂, ..., v_k;v₁ + v₂ + ... + v_k = 1.

Ряд значений признака, или вариант, полученных вследствие массового обследования однородных вещей или явлений, размещенных в порядке возрастания или убывания их величин, вместе с соответствующими частотами (или относительными частотами) называют вариационным рядом.

Если в вариационном ряде значения признака (варианты) заданы в виде отдельных конкретных чисел, то такой ряд называют дискретным.

42. Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события А определяется формулой W (А) = m / n,

где m - число появлений события, n - общее число испытаний. вероятность вычисляют до опыта, а относительную частоту - после опыта.

Если ряд распределения построен по количественному признаку, то такой ряд называют вариационным. Построить вариационный ряд - значит упорядочить количественное распределение единиц совокупности по значениям признака, а затем подсчитать числа единиц совокупности с этими значениями (построить групповую таблицу). Выделяют три формы вариационного ряда: ранжированный ряд, дискретный ряд и интервальный ряд. Если признак имеет непрерывное изменение (размер дохода, стаж работы, стоимость основных фондов предприятия и т.д., которые в определенных границах могут принимать любые значения), то для этого признака нужно строить интервальный вариационный ряд. Частота (частота повторения) - число повторений отдельного варианта значений признака, обозначается f_i

43. Полигон: При построении полигона на горизонтальной оси (ось абсцисс) откладывают значения варьирующего признака, а на вертикальной оси (ось ординат) — частоты или частости. (\/\) Другим распространенным способом графического представления является полигон частот.

Полигон частот образуется ломаной линией, соединяющей точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов, срединные значения откладываются по оси х, а частоты – по оси у.

Из сравнения двух рассмотренных способов графического представления эмпирических распределений следует, что для получения полигона частот из построенной гистограммы нужно середины вершин прямоугольников, образующих гистограмму, соединить отрезками прямых.

Гистограмма: Для построения гистограммы по оси абсцисс указывают значения границ интервалов и на их основании строят прямоугольники, высота которых пропорциональна частотам (или частостям). ()Гистограмма используется для графического представления распределений непрерывно варьирующих признаков и состоит из примыкающих друг к другу прямоугольников. Основание каждого прямоугольника равно ширине интервала группировки, а высота его такова, что площадь прямоугольника пропорциональна частоте (или частости) попадания в данный интервал. Если ряд безинтервальный, то ширина всех столбцов выбирается произвольной, но одинаковые. Таким образом, высоты прямоугольников должны быть пропорциональны величинам

44.
Накопленные частоты ( или частости) вариантов ( интервалов) получаются суммированием всех частот ( или частостей) вариантов ( интервалов), предшествующих данному с частотой ( частостью) этого варианта. Накопление частоты можно получить не только в восходящем порядке, но и в нисходящем, тогда частоты ( или частости) суммируются снизу вверх. Накопленной частоты, т. е. число значений, которые попали в этот интервал и все предшествующиеЗначения накопленных относительных частот, т. е. отношений накопленных частот к объему совокупности данных.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения х относительную частоту события Х

F*(x)=n_х/n

где n_х – число вариант, меньшее х, n – объем выборок. Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

Распределение признака в вариационном ряду по накопленным частотам (частостям) изображается с помощью кумуляты.

Кумулята или кумулятивная кривая в отличие от полигона строится по накопленным частотам или частостям. При этом на оси абсцисс помещают значения признака, а на оси ординат — накопленные частоты или частости .

45. Выборка или выборочная совокупность — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных изгенеральной совокупности для участия в исследовании.

Характеристики выборки:

§ Качественная характеристика выборки – кого именно мы выбираем и какие способы построения выборки мы для этого используем.

§ Количественная характеристика выборки – сколько случаев выбираем, другими словами объём выборки.

Выборочная дисперсия в математической статистике — это оценка теоретической дисперсии распределения на основе выборки. Различают выборочную дисперсию и несмещённую, или исправленную, выборочные дисперсии.

Среднеквадрати́ческое отклоне́ние (синонимы: среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие термины: станда́ртное отклоне́ние,станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно еёматематического ожидания

46. статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.

Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям: оценка должна быть несмещенной, эффективной и состоятельной.

Несмещенной называют статистическую оценку , математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, т. е.

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объема (n велико) к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называют статистическую оценку, которая при стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при стремится к нулю, то такая оценка оказывается и состоятельной.

47. Генеральной средней называют среднее арифметическое значений признака генеральной совокупности. Генеральной дисперсией D_г называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения . статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.

Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям: оценка должна быть несмещенной, эффективной и состоятельной.

Поясним каждое из понятий.

Несмещенной называют статистическую оценку Q^*, математическое ожидание которой равно оцениваемому параметру Q при любом объеме выборки, т. е.

M(Q^*) = Q.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки п) имеет наименьшую возможную дисперсию.

Состоятельной называют статистическую оценку, которая при п®¥ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при п®¥ стремится к нулю, то такая оценка оказывается и состоятельной.

48. Интервальной называют оценку, которая определяется двумя числами - концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.

Пусть найденная по данным выборки статистическая характеристика служит оценкой неизвестного параметра . Будем считать постоянным числом ( может быть и случайной величиной). Ясно, что тем точнее определяет параметр , чем меньше абсолютная величина разности . Другими словами, если и , то чем меньше д , тем оценка точнее.

Таким образом, положительное число д характеризует точность оценки

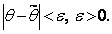
Отсюда видно, что чем меньше , тем точнее характеризуется неизвестный параметр θ с помощью выборочной оценки 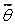. Следовательно, число  характеризует точность оценки параметра θ.

Надежность выполнения неравенства 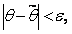оценивается числом  (α = 1 – γ), которое называют доверительной вероятностью

Интервал в интервальной оценке называется ДОВЕРИТЕЛЬНЫМ ИНТЕРВАЛОМ, задаваемая исследователем вероятность называется ДОВЕРИТЕЛЬНОЙ ВЕРОЯТНОСТЬЮ

49. Интервальное оценивание — один из видов статистического оценивания, предполагающий построение интервала, в котором с некоторой вероятностью находится истинное значение оцениваемого параметра. ИНТЕРВАЛЬНАЯ ОЦЕНКА - оценка представляемая интервалом значений, внутри которого с задаваемой исследователем вероятностью находится истинное значение оцениваемого параметра.

50. Статистической гипотезой называется любое предположение относительно функции распределения наблюдаемых случайных величин.

Если статистическая гипотеза полностью определяет функцию распределения наблюдаемых случайных величин, она называется простой статистической гипотезой . Если статистическая гипотеза не является простой, она является сложной . Сложная гипотеза указывает некоторое множество распределений. Обычно это множество распределений обладает определенными свойствами. Нулева́я гипо́теза — гипотеза, которая проверяется на согласованность с имеющимися выборочными (эмпирическими) данными. Часто в качестве нулевой гипотезы выступают гипотезы об отсутствии взаимосвязи или корреляции между исследуемыми переменными, об отсутствии различий (однородности) в распределениях (параметрах распределений) двух и/или более выборках. В стандартном научном подходе проверки гипотез исследователь пытается показать несостоятельность нулевой гипотезы, несогласованность её с имеющимися опытными данными, то есть отвергнуть гипотезу. При этом подразумевается, что должна быть принята другая,альтернативная (конкурирующая), исключающая нулевую, гипотеза. Используется при статистической проверке

Ошибки первого рода (и ошибки второго рода в математической статистике — это ключевые понятия задач проверки статистических гипотез. Уровень значимости статистического теста — допустимая для данной задачи вероятность ошибки первого рода (ложноположительного решения, false positive), то есть вероятность отклонить нулевую гипотезу, когда на самом деле она верна.

Другая интерпретация: уровень значимости — это такое (достаточно малое) значение вероятности события, при котором событие уже можно считать неслучайным.

31) Непрерывные случайные величины

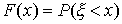
Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х. Случайная величина называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция* , удовлетворяющая для любых значений x равенству

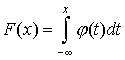
Функция называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если x1<x2,

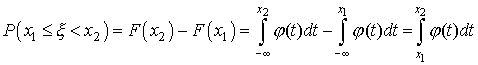
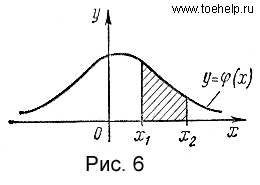
Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств равна площади криволинейной трапеции с основанием [x1,x2], ограниченной сверху кривой (рис. 6).

Так как 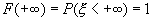, то

,

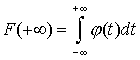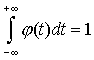
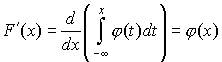
Заметим, что для непрерывной случайной величины функция распределения F(х) непрерывна в любой точке х, где функция 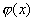непрерывна. Это следует из того, что F(х) в этих точках дифференцируема.

полагая x1=x, 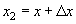имеем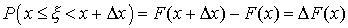

В силу непрерывности функции F(х) получим, что

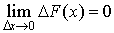
Следовательно

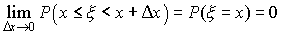
Таким образом, вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю.

Отсюда следует, что события, заключающиеся в выполнении каждого из неравенств. , , , .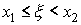

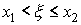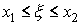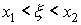Имеют одинаковую вероятность, т.е.

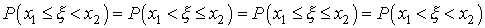
В самом деле, например,

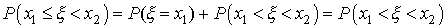
так как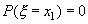

32)Числовые характеристики непрерывных случайных величин

Математическим ожиданием непрерывной случайной величины 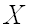возможные значения которой принадлежат отрезку 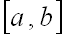называют определенный интеграл.

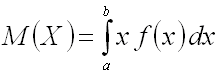
Если возможные значения принадлежат всей числовой оси, то

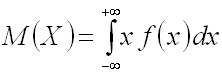
(предполагается, что несобственный интеграл, стоящий в правой части равенства, существует).

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные непрерывной случайной величины 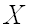принадлежат отрезку 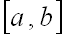, то

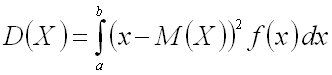
Если возможные значения принадлежат всей числовой оси, то

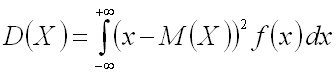
(предполагается, что несобственный интеграл, стоящий в правой части равенства, существует).

Средним квадратическим отклонением непрерывной случайной величины называют, как и для величины дискретной, квадратный корень из дисперсии:

.

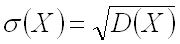33) Равномерное распределение.

Пусть сегмент [a,b] оси Ox есть шкала некоторого прибора. Допустим, что вероятность попадания указателя в некоторый отрезок шкалы пропорциональна длине этого отрезка и не зависит от места отрезка на шкале. Отметка указателя прибора есть случайная величина 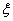могущая принять любое значение из сегмента [a,b]. Поэтому 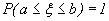. Если, далее, x1 и x2 (x1<x2) - две любые отметки на шкале, то согласно условию имеем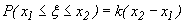

где k - коэффициент пропорциональности, не зависящий от x1 и x2, а разность x2-x1, - длина сегмента [x1,x2]. Так как при x1=a и x2=b имеем 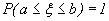то k(b-a)=1, откуда k=1/(b-a). Таким образом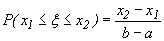

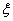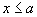Теперь легко найти функцию F(x) распределения вероятностей случайной величины Если то 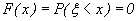так как 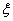не принимает значений, меньших a. Пусть теперь 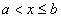По аксиоме сложения вероятностей 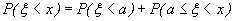Согласно формуле (26), в которой принимаем x1=a, x2=х имеем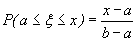

Так как 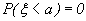то при 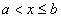получаем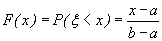

Наконец, если x>b, то F(x)=1, так как значения лежит на сегменте [a,b] и, следовательно, не превосходят b. Итак, приходим к следующей функции распределения: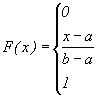

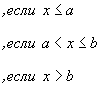
График функции F(x) представлен на рис. 9.

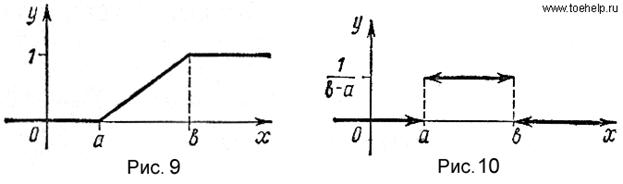
Плотность распределения вероятностей найдем по формуле .Если x<a или x>b, то 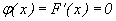Если a<x<b, то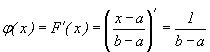

Таким образом,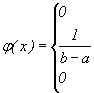

График функции изображен на рис. 10. Заметим, что в точках a и b функция 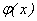терпит разрыв.

34) Показательное распределение:

Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.

Случайная величина 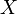имеет экспоненциальное распределение с параметром 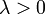если её плотность имеет вид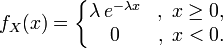

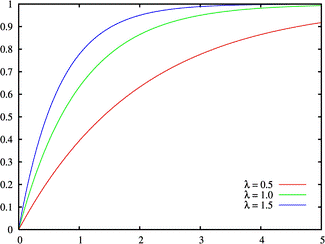
Функция распределения:

Интегрируя плотность, получаем функцию экспоненциального распределения: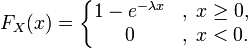

Плотность вероятности

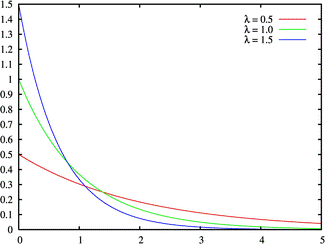
Функция распределения

35) Показательный закон надёжности

Экспоненциальный (показательный) закон. В основном периоде эксплуатации отказы происходят от случайных факторов (попадание посторонних предметов, сочетание внешних факторов и др.) и носят внезапный характер. Время же проявления отказа не связано с предыдущей наработкой изделия. Интенсивность отказов для этого периода может быть принята величиной постоянной (рис. 4.2, а).

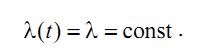
Тогда вероятность безотказной работы по уравнению (4.10)

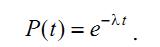
Плотность распределения отказов

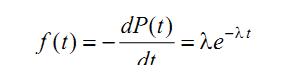
Среднее время безотказной работы

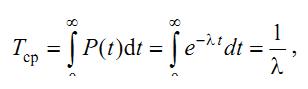
Экспоненциальный закон распределения отказов, выраженный формулами и , справедлив для описания потока отказов с постоянной интенсивностью. Понятие потока отказов применяют для восстанавливаемых в процессе эксплуатации изделий. Величина ср T для потока отказов представляет среднюю наработку на один отказ.

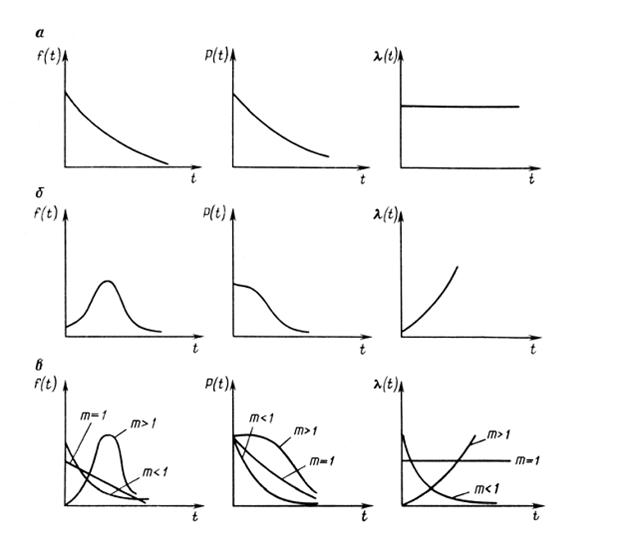
Рис. 4.2. Графики распределения случайных величин f (t) и показателей

надежности – вероятности безотказной работы P(t) и интенсивности отказов λ(t) при рас-

пределениях: a – экспоненциальном; б – нормальном; в – Вейбулла.

Вероятность безотказной работы элемента на интервале времени длительностью t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t (при заданной интенсивности отказов λ).

Для доказательства свойства введем обозначения событий:

А — безотказная работа элемента на интервале (0,t) длительностью t₀;

В — безотказная работа на интервале (t₀, t₀+t) длительностью t.

Тогда АВ — безотказная работа на интервале

(0, t₀+t) длительностью t₀+t.

Найдем вероятности

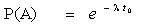
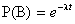
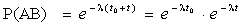
Найдем условную вероятность того, что элемент будет работать безотказно на интервале (t₀, t₀+t) прн условии, что он уже проработал безотказно иа предшествующем интервале (0, t₀)

.

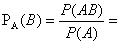
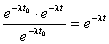36) Нормальное распределение

Нормальное распределение, также называемое гауссовым распределением или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:

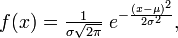
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

Если случайные величины 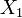и 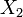независимы и имеют нормальное распределение с математическими ожиданиям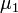и и 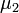и дисперсиям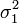и и 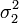соответственно, то 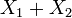также имеет нормальное распределение с математическим ожиданием 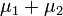и дисперсией .

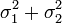Плотность вероятности

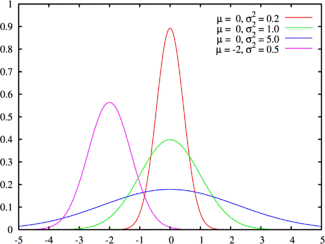
Зеленая линия соответствует стандартному нормальному распределению

Функция распределения

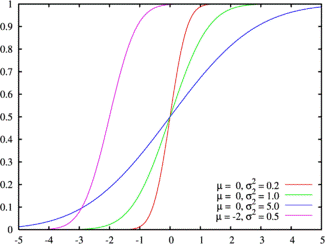
Правило трех сигм

Правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

P(|X − a| < δ) = 2Φ 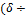σ)

положив δ = σt. В итоге получим

P(|X − a| < σt) = 2Φ (t).

Если t = 3 и, следовательно, σt = 3σ, то

P(|X − a| < 3σ) = 2Φ (3) = 2 · 0.49865 = 0.9973,

На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.

37) Понятие о теореме Ляпунова

Теорема Ляпунова — теорема в теории вероятностей, устанавливающая некоторые общие достаточные условия для сходимости распределения сумм независимых случайных величин к нормальному закону.

если случайная величина 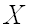представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то 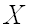имеет распределение, близкое к нормальному.

Часто приходится иметь дело с такими случайными величинами, которые являются суммами большого числа независимых случайных величин. При некоторых весьма общих условиях оказывается, что эта сумма имеет распределение, близкое к нормальному, хотя каждое из слагаемых может не подчиняться нормальному закону распределения вероятностей. Эти условия были найдены Ляпуновым и составляют содержание теоремы, названной его именем.

Пусть с 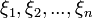последовательность попарно независимых случайных величин с математическими ожиданиями M 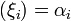и дисперсиями D 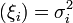, причём эти величины обладают следующими двумя свойствами:

1) Существует такое число L, что для любого i имеет место неравенство 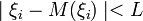т, е. все значения случайных величин, как говорят, равномерно ограничены, относительно математических ожиданий;

2) Сумма 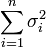неограниченно растёт при .

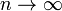Тогда при достаточно большом n сумма 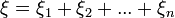имеет распределение, близкое к нормальному.

Пусть 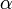и 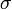математическое ожидание и дисперсия случайной величины 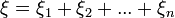Тогда:

.
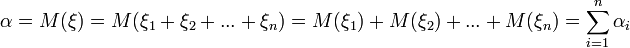
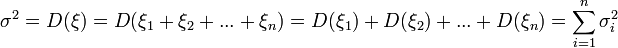
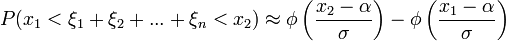